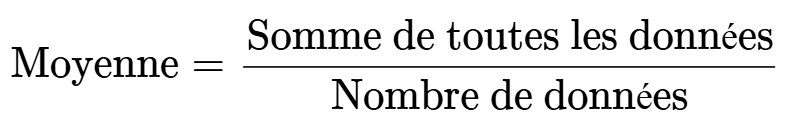Best Of
Re: Question
les arteres transportes le sang du coeur aux organes alors que les veines ramene le sang des organes vers le coeur.
arteres; sang coeur-->organes
veine; sang organes-->coeur
Question
Merci pour les prof qui sont venu dans l école saint bernadette soubirou je suis un éléve et 2 prof sont venu et nous on bien aider☺️☺️☺️☺️☺️
Question
Comment je peux trouver la règle d'un fonction exponentielle si j'ai juste le y et la base?
( dans mon cas la variable y=911,25$ et la base 1,5)
La situation veut qu'on trouve le nombre d'heure si le prix est des 911,25$ et le problème dit je cite, "le coût du nettoyage du polluant b après le premier incident était de 911,25$".
x:temps écoulé depuis le déversement
y:coût du nettoyage
merci d'avance :)
Re: Question
Alloprof est vraiment pertinent et d'une aide cruciale en effet! N'hésite pas à poser tes questions si tu en as! ;)
Re: Question
Salut!
La priorité des opérations est un ordre d'opérations à suivre lorsqu'on veut manipuler une chaîne d'opération.
PEMDAS est un truc mnémotechnique pour se souvenir de l'ordre que nous devons suivre dans une chaîne d'opérations.
P : Parenthèses
E : Exposants
MD : Multiplication et Division
AS : Addition et soustraction
Selon ce truc, la première chose à calculer est ce qui est entre parenthèses, suivi des exposants. Ensuite, on doit calculer les multiplications et les divisions dans l'ordre où elles apparaissent (de gauche à droite). Enfin, on calcule les additions et les soustractions dans l'ordre dans lequel elles apparaissent aussi (de gauche à droite).
Voici un petit exemple :
(5 × 2 − 3 + 10) + 32 − (10 ÷ 5 × 2) − 1 + 22
Commençons par résoudre ce qui est entre parenthèses (en respectant PEMDAS) :
(5 × 2 - 3 + 10) + 32 − (10 ÷ 5 × 2) − 1 + 22
On effectue d'abord la multiplication de 5 par 2. Ensuite, nous faisons la soustraction, car elle vient avant l'addition.
= (10 -3 + 10) + 32 − (10 ÷ 5 × 2) − 1 + 22
= (10 - 3 + 10) + 32 − (10 ÷ 5 × 2) − 1 + 22
= (7 + 10) + 32 − (10 ÷ 5 × 2) − 1 + 22
= (17) + 32− (10 ÷ 5 × 2) − 1 + 22
On fait la même chose pour la seconde parenthèse :
17 + 32 − (10 ÷ 5 × 2) − 1 + 22
Nous effectuons d'abord la division de 10 par 5, car elle vient avant la multiplication.
17 + 32 − (2 × 2) − 1 + 22
17 + 32 − (4) − 1 + 22
Terminons par les additions et les soustractions dans l'ordre dans lequel elles apparaissent (de gauche à droite) :
17 + 32 − 4 − 1 + 22 = 66
Voici une fiche sur cette notion qui pourrait t'être utile : La priorité des opérations | Primaire | Primaire | Alloprof
En ce qui concerne la multiplication de nombres décimaux, elle s'effectue comme une multiplication normale ! Ensuite, tu comptes le nombre de décimales au total dans les deux nombres décimaux que tu as multipliés pour savoir combien de chiffres se trouvent après la virgule dans ta réponse. Donc, voici les étapes à suivre :
1) Effectue ta multiplication normalement, en colonne, sans te soucier des virgules (comme si tu ne les voyais pas).
2) Une fois ta réponse obtenue, compte le nombre de chiffres qui se trouvent après la virgule dans les facteurs de multiplication. Ça te dira le nombre de chiffres dans la réponse qui vont se trouver après la virgule.
3) Place la virgule au bon endroit dans ta réponse.
Je t'invite à consulter notre fiche sur la multiplication des nombres décimaux pour avoir un exemple concret : Multiplier des nombres décimaux | Primaire | Primaire | Alloprof
De plus, tu dois aussi suivre la même méthode qu'avec des nombres entiers pour la division de nombres décimaux!
Cependant, si c'est le diviseur qui est un nombre décimal (le nombre par lequel on divise, le nombre après le ÷), tu peux transformer ce nombre décimal en multipliant le diviseur et le dividende par une puissance de 10. Si le nombre décimal a 1 chiffre après la virgule, tu dois multiplier par 10 (\(10^1\)), s'il en a 2, tu multiplies par 100 (\(10^2\)), s'il en a 3, tu multiplies par 1000 (\(10^3\)), etc.
Par exemple, si nous voulons effectuer la division suivante :
$$ 31,048 \div 7,39 $$
Le diviseur, soit 7,39, possède 2 chiffres après la virgule, nous allons donc multiplier le diviseur et le dividende par 100, comme ceci :
$$31,048 \div 7,39 = \frac{31,048}{7,39}$$
$$ = \frac{31,048\times 100}{7,39\times 100} $$
$$ = \frac{3104,8}{739} $$
Tu peux ensuite effectuer cette division comme à l'habitude à l'aide de la méthode des crochets.
Je t'invite à consulter les fiches suivantes :
- Diviser des nombres | Primaire | Primaire | Alloprof
- Diviser des nombres décimaux | Primaire | Primaire | Alloprof
Pour calculer une moyenne, il faut suivre la formule suivante :
Voici un exemple :
Voici la température des trois derniers jours : 23 degrés, 19 degrés et 21 degrés. Quelle est la moyenne de la température des trois derniers jours ?
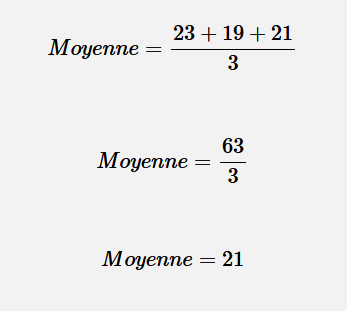
Appliquons donc cette formule à ce problème :
Il a donc fait en moyenne 21 degrés.
Voici une fiche qui pourrait t'être utile : La moyenne | Secondaire | Alloprof
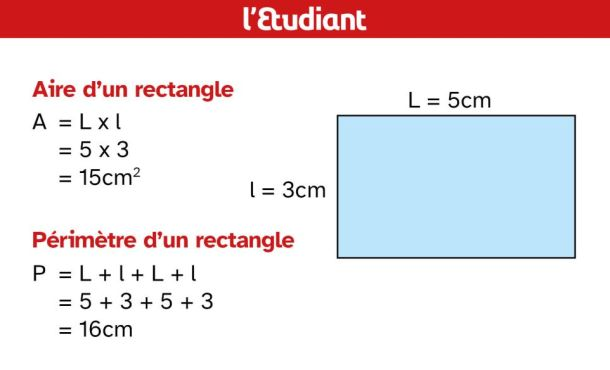
Finalement, en ce qui concerne l'aire, elle correspond à la mesure de la superficie d’une surface. Pour calculer l'aire d'une figure, il faut utiliser la bonne formule, selon le type de figure que tu as (carré, rectangle, triangle, etc.). Au primaire, on apprend uniquement à calculer l'aire d'un rectangle et d'un carré, et pour cela, il suffit de multiplier la longueur par la largeur. Voici un exemple :
Ces fiches pourraient t'aider :
J'espère que cela t'aide! Si des questions persistent après ta lecture, reviens nous voir! :)
Question
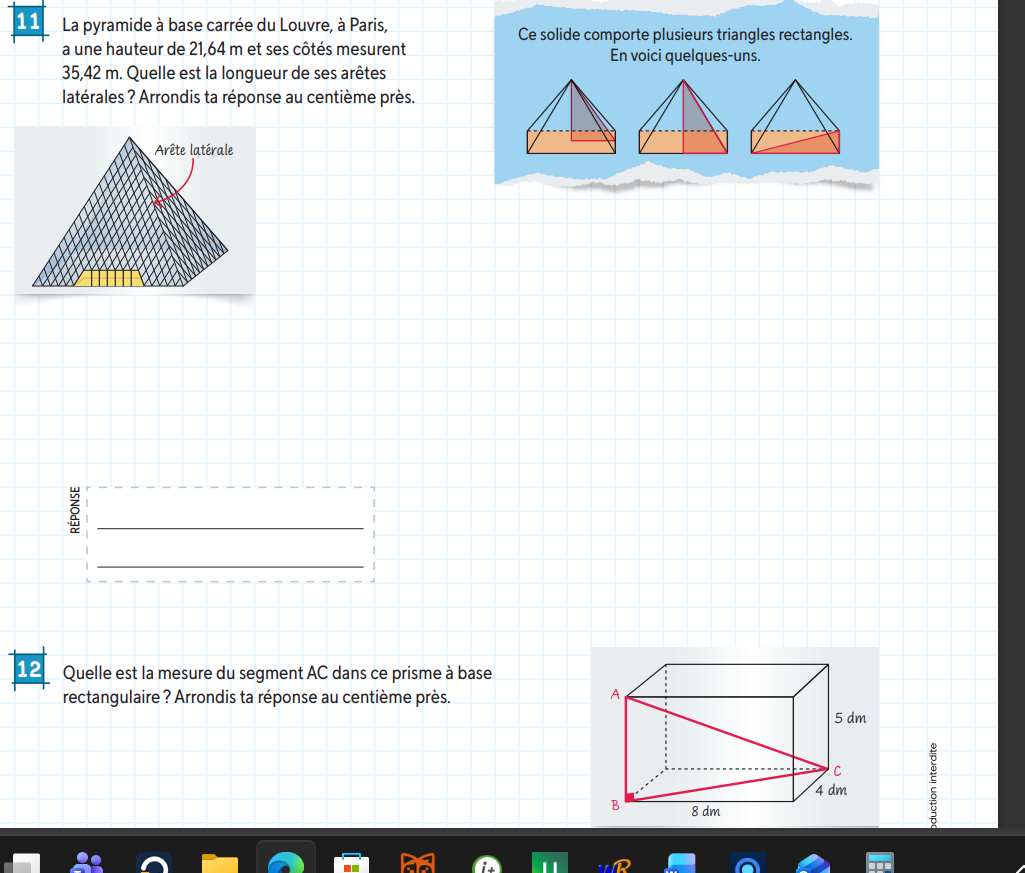
Bonjour, j'espere que vous allez bien aujourd'hui. Pouriez -vous m'aider a resoudre ce probleme de mathematiques ?
Merci !