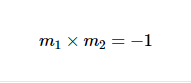Best Of

Allo MentheRose8303,

Merci pour ta question!

Pour commencer, tu dois faire la parenthèse. Commence par le 40 divisé par 2.

Ensuite, tu peux faire la multiplication avec le 3.

Continue avec la multiplication de ce qui est au dénominateur de la fraction.

Finalement, tu peux faire la division.

J'espère t'avoir aidé!

Lea-Kim

Bonjour, Marie !

La réponse dépend de l'aire des friandises: on ne sait pas si elles sont très petites ou grosses comme des gommes à mâcher.

L'aire latérale d'un cône est de \(A_L = \pi r a  \).

https://www.alloprof.qc.ca/fr/eleves/bv/mathematiques/l-aire-des-cones-m1488

Tu as r=14/2 et a=√(r²+h²).

Cependant, tu as un demi-cône, donc tu divises par 2 le résultat.

En plus, la coupure crée un triangle, donc calcule son aire.

Tu dois aussi trouver l'aire du demi-cercle.

Salut, Marie !

Il faudrait avoir l'image pour comprendre où se trouve la poutre ! N'hésite pas à renvoyer une photo avec le schéma.

Supposons qu'elle fait toute la hauteur du cylindre et de la demi-sphère.

L'aire d'une base d'un cylindre est donnée par \( A_{ \text{b cylindre}} = \pi r^2\).

Sachant que l'aire de la base est de 57,76πm², trouve le rayon r.

L'aire latérale est \( A_{ \text{L cylindre}} = 2 \pi r h\).

https://www.alloprof.qc.ca/fr/eleves/bv/mathematiques/l-aire-des-cylindres-m1487

L'aire latérale d'une demi-sphère est \( A_{ \text{L demie-sphère}} =\frac{4 \pi r^2 }{2} \).

https://www.alloprof.qc.ca/fr/eleves/bv/mathematiques/l-aire-d-une-sphere-m1486

En additionnant ces deux dernières, on a 480,32πm². Ainsi, tu peux trouver h.

Ayant toutes les inconnues, trouve la hauteur de la poutre !

VC

Allo PoutineExemplaire1042,

Merci pour ta question!

Tu dois commencer par développer tes polynômes exposant 4. Ensuite, tu auras des éléments qui vont s'annuler et tu pourras simplifier.

J'espère t'avoir aidé!

Lea-Kim

Salut ZombieZen9487,

Merci pour ta question! 😉

Dans cette situation, tu peux imaginer le point P comme le point de rencontre entre les droites AB et CP. Il faut donc que tu trouves chacune des fonctions et leur point de rencontre.

Pour ce qui est de la droite AB, tu as tout ce qu'il te faut pour calculer la pente et ensuite trouver l'ordonnée à l'origine afin d'obtenir son équation. Cependant, pour trouver la pente de CP, tu dois utiliser une propriété des droites perpendiculaires: le produit de leur pente est égal à -1.

Ce contenu est protégé par le droit d'auteur. Toute reproduction à l'extérieur des forums Alloprof est interdite et pourra être considérée comme une violation du droit d'auteur.

À l'aide de la valeur de pente que tu as trouvée pour l'équation AB et de cette propriété, tu peux trouver la pente de CP. À l'aide de cette mesure et du point C, tu peux trouver son ordonnée à l'origine afin de trouver son équation.

Il ne te reste plus qu'à trouver les coordonnées de P en utilisant tes deux équations pour former un système d'équations linéaires.

Voici une fiche à ce sujet qui peut te dépanner :

J'espère que ça t'aide et n'hésite pas à nous réécrire si tu as d'autres questions! 😊

Anthony B.