Matières
Niveaux
L'aire des cylindres
Fiche | Mathématiques
Secondaire
2-3
Table des matières
L’aire d’une base
Selon sa construction et sa définition, l'aire des bases d'un cylindre sera toujours calculée en fonction des disques qui le définissent. Par ailleurs, il existe déjà une formule pour calculer la superficie de cette figure plane.
||A_b = \pi r^2|| où ||\begin{align}A_b&: \text{Aire d’une base}\\r&: \text{rayon}\end{align}||
Selon le contexte, il faut considérer soit l’une, soit les deux bases du cylindre.
Afin d'avertir les véhicules qui le suivent, un camionneur transportant des troncs d'arbres cylindriques peint en rouge l'extrémité du tronc qui dépasse le plus de son chargement.
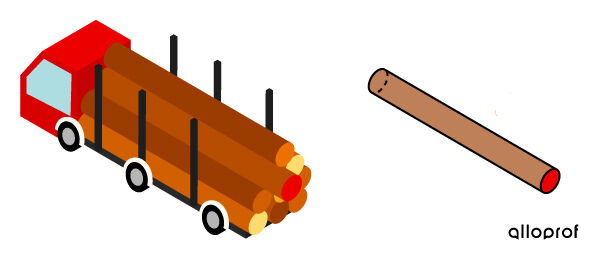
Quelle est la mesure de la surface recouverte de peinture sachant que les troncs ont un rayon moyen de 15 cm?
-
Identifier les faces concernées
Dans le cas présent, seule l’une des bases est concernée. Ainsi, il suffit de calculer l'aire d'un seul disque. -
Appliquer la formule ||\begin{align} A_b &= \pi r^2\\ &= \pi (15)^2\\ &\approx 706{,}86\ \text{cm}^2\end{align}||
-
Interpréter la réponse
La surface recouverte de peinture a une superficie d'environ |706{,}86\ \text{cm}^2.|
Dans un autre contexte, on aurait pu calculer l'aire des 2 bases. On suivrait alors la même démarche en s'assurant de multiplier l'aire de la base par 2 au moment d'interpréter la réponse.
L'aire latérale
En se basant sur le développement du cylindre, on peut en déduire que la face latérale est en fait un rectangle qui entoure chacune des bases circulaires.
On peut représenter cet enroulement de la façon suivante :
Dans ce dessin, on voit que||\begin{align} \color{#3A9A38}{\text{Base de la face latérale}} &= \color{#3A9A38}{\text{Circonférence du cercle}}\\
\color{#51B6C2}{\text{Hauteur de la face latérale}} &= \color{#51B6C2}{\text{Hauteur du cylindre}}\\\\
\Rightarrow\ \text{Aire de la face latérale} &= \color{#3A9A38}{\text{Circonférence}}\times \color{#51B6C2}{\text{Hauteur}}\end{align}||
En tenant compte de ces informations, on peut dégager la formule d'aire suivante.
||A_L = 2 \pi r h|| où ||\begin{align} A_L&:\text{Aire latérale}\\r&:\text{rayon de la base} \\ h &: \text{hauteur du cylindre} \end{align}||
Pour mettre le tout en pratique, on peut se fier à la démarche suivante.
Pour apposer la marque de commerce du fabricant sur ses crayons marqueurs, le directeur commercial décide de poser un autocollant sur toute la surface latérale du marqueur.
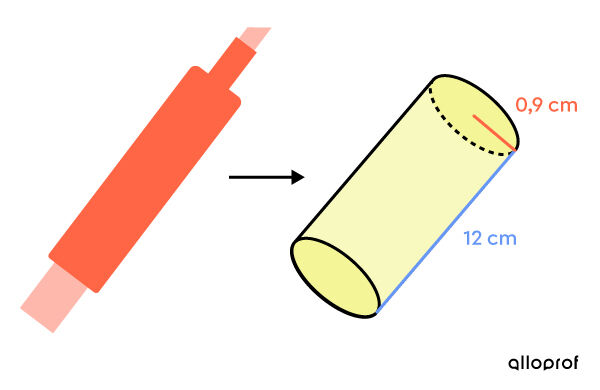
Avec ces informations, détermine la superficie de cet autocollant.
-
Identifier le solide
Le surligneur est de forme cylindrique. Dans ce problème, il faut calculer l'aire latérale du cylindre. -
Appliquer la formule ||\begin{align} A_L &= 2 \pi r h\\ &= 2 \pi (0{,}9) \times 12\\ &\approx 67{,}86 \ \text{cm}^2\end{align}||
-
Interpréter la réponse
L'autocollant a une surface d'environ |67{,}86 \ \text{cm}^2.|
L'aire totale
Comme c’est le cas pour les prismes, il faut additionner l'aire des bases et l'aire latérale du solide étudié pour trouver son aire totale.
||A_T = 2A_b + A_L|| où ||A_T:\text{Aire totale}||
Une fois de plus, cette formule peut changer selon le contexte. Par exemple, il peut arriver qu'une seule des deux bases soit à considérer.
Dans le but d'innover, une compagnie qui fabrique des gourdes d'eau laisse le soin à ses clients d'imprimer les motifs qu'ils veulent sur toutes les surfaces de la bouteille.
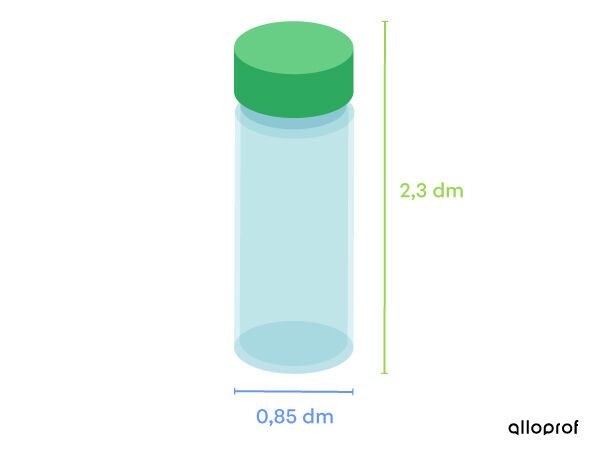
Selon ce modèle, quelle est la mesure de la surface sur laquelle les clients peuvent imprimer des motifs?
-
Identifier les faces concernées
Pour ce contexte, toutes les faces du cylindre sont à considérer. -
Calculer l'aire d'une base ||\begin{align} A_b &= \pi r^2\\ &= \pi \left(\dfrac{0{,}85}{2}\right)^2\\ &\approx 0{,}57\ \text{dm}^2\end{align}||
-
Calculer l'aire latérale ||\begin{align} A_L &= 2 \pi r h\\ &= 2 \pi \left(\dfrac{0{,}85}{2}\right) \times 2{,}3\\ &= 0{,}85\pi \times 2{,}3\\&\approx 6{,}14\ \text{dm}^2\end{align}||
-
Calculer l'aire totale ||\begin{align}A_T &= 2 A_b + A_L\\ &= 2 (0{,}57) + 6{,}14\\ &= 7{,}28\ \text{dm}^2\end{align}||
-
Interpréter la réponse
Il est possible d'imprimer des motifs sur une surface de |7{,}28 \ \text{dm}^2.|
Dans d'autres cas, on pourrait s'intéresser à l’une des mesures de la base ou encore à la hauteur du cylindre alors que l’aire totale est donnée. C’est ce qu’on appelle trouver une mesure manquante d'un cylindre à partir de l'aire. Dans ce cas, la démarche est un peu différente, mais il demeure essentiel de se rappeler la formule de l’aire totale associée aux cylindres.
Vidéo
L'aire des cylindres
Moments dans la vidéo :
- 00:00-La formule de l’aire
- 01:10-Le développement d’un cylindre
- 02:15-Exemple