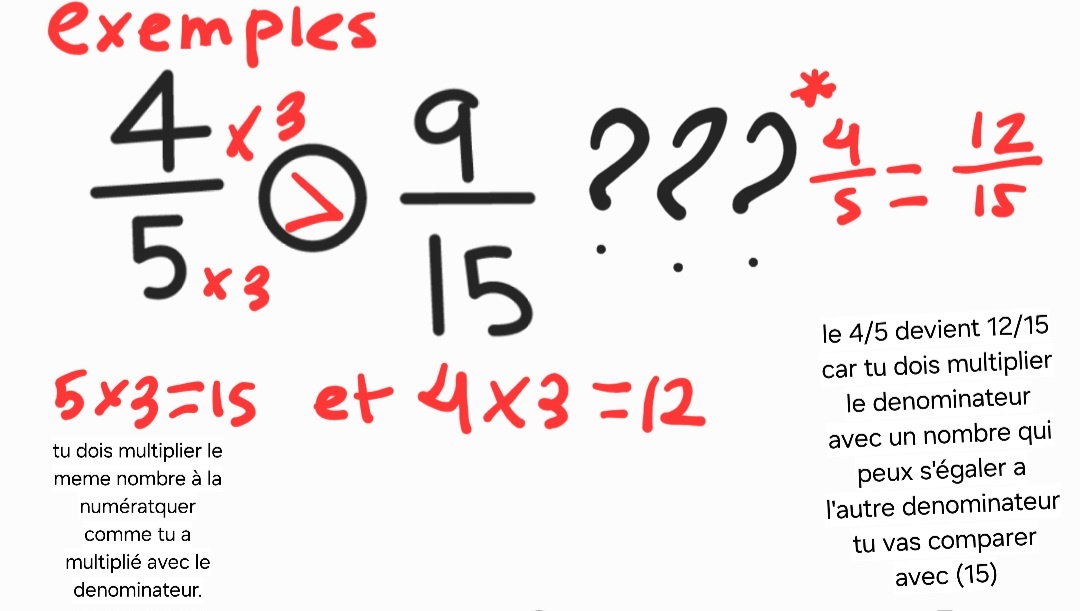Best Of
Re: Question
Salut Avocat Supra!
Voici ma demarche! (exemple)
N'hésite pas a me poser des questions ça me rendra encore du plaisir pour vous aider!
À bientôt!
Kiwi☆
Re: Question
Salut KiwiSigma6383!
Oui il y aura un examen du ministère en lecture en 6 année. Pour t'aider, tu peux jouer à grimoire. Tu peut aussi lire un livre et demander à ton parent ou à ton tuteur de te poser des questions en lien avec le livre.
Re: Question
Bonjour DiamantResponsable4969,
Merci d’utiliser la Zone d’entraide!
🧠 Qu’est-ce que le subjonctif présent ?
Le subjonctif présent est un temps de verbe utilisé pour exprimer des actions qui ne sont pas certaines. Il est souvent employé après des expressions qui indiquent un souhait, une nécessité, une émotion ou un doute. Par exemple :
- Souhait : Je souhaite que tu réussisses ton examen.
- Nécessité : Il faut que nous finissions nos devoirs.
- Émotion : Je suis content que tu viennes à ma fête.
- Doute : Je ne pense pas qu’il soit là.
🛠️ Comment former le subjonctif présent?
Pour conjuguer un verbe au subjonctif présent, on suit généralement ces étapes :
- Prendre la forme «ils» au présent de l’indicatif : Par exemple, pour le verbe parler, «ils parlent».
- Retirer la terminaison «-ent» : Cela donne le radical «parl-».
- Ajouter les terminaisons du subjonctif présent :
- Je : -e → que je parle
- Tu : -es → que tu parles
- Il/Elle/On : -e → qu’il parle
- Nous : -ions → que nous parlions
- Vous : -iez → que vous parliez
- Ils/Elles : -ent → qu’ils parlent
Note : Certains verbes ont des formes irrégulières au subjonctif. Par exemple:
- être : que je sois, que tu sois, qu’il soit, que nous soyons, que vous soyez, qu’ils soient
- avoir : que j’aie, que tu aies, qu’il ait, que nous ayons, que vous ayez, qu’ils aient
Pour approfondir ta compréhension et t’exercer, voici une ressource utile: https://www.alloprof.qc.ca/fr/eleves/bv/francais/le-subjonctif-present-0-f1891?
Ne lâche pas,
ScorpionComique4949.
Re: Question
Allo FramboiseAlerte5917,
Merci pour ta question!
On peut simplement dessiner 28 cases. Ensuite, on divise en 4 parties égales.
J'espère que ça t'aidera!
Lea-Kim
Re: Question
Salut PerroquetComique2897,
Merci pour pour cette nouvelle question. 🤩
Cette fiche explicative devrait te renseigner suffisamment sur le sujet. Je t'invite donc à la consulter!
En espérant que cela répond à ta question. Si tu en as d'autres, n'hésite surtout pas à nous réécrire, il nous fera plaisir de t'aider à nouveau! Ne lâche pas dans ta compréhension de la Christianisation de l'Occident! :)
À bientôt,
Océane :)
Re: Question
Salut PerroquetComique2897!
Merci pour ta question. 🤩
Les redevances seigneuriales sont une autre importante source de revenus pour l’Église puisqu’elle possède plusieurs seigneuries. Elle peut donc bénéficier des revenus de celles-ci. Ces redevances prennent plusieurs formes. Il y a d’abord le cens qui est un montant d’argent qu’un paysan doit payer à son seigneur. Le cens est en lien avec la tenure (terre agricole) accordée au paysan par le seigneur. La corvée est une autre forme de paiement et correspond à des jours de travail obligatoire pour les paysans durant lesquels ils réalisent des travaux pour leur seigneur sur ses terres. Il existe aussi d’autres formes de redevances telles que les taxes sur l’utilisation du moulin, du four, du pressoir, etc.
Ces multiples formes de revenus permettent à l’Église chrétienne de devenir une puissance économique en Europe.
Pour plus d'informations à ce sujet, je t'invite à consulter cette fiche explicative!
En espérant que cela répond à ta question. Si tu en as d'autres, n'hésite surtout pas à nous réécrire, il nous fera plaisir de t'aider à nouveau!
À bientôt,
Océane :)
Re: Question
Salut PerroquetComique2897!
Merci pour ta question. 🤩
Tu retrouveras la réponse dans cette fiche explicative dans le paragraphe portant sur la papauté!
En espérant que cela répond à ta question. Si tu en as d'autres, n'hésite surtout pas à nous réécrire, il nous fera plaisir de t'aider à nouveau!
À bientôt,
Océane :)
Re: Question
Salut PercheHonorable3167!
Merci pour ta question. 🤩
La lecture de cette fiche explicative devrait te permettre de discerner les conséquences de l'Église sur le souverain ainsi que l'influence de l'Église sur le peuple!
De plus, pour le mot "église", on utilise la majuscule lorsqu'on fait référence à l'institution religieuse, tandis qu'on utilise la minuscule lorsqu'on fait référence au bâtiment!
En espérant que cela répond à ta question. Si tu en as d'autres, n'hésite surtout pas à nous réécrire, il nous fera plaisir de t'aider à nouveau! Bon succès dans cet examen!
À bientôt,
Océane :)
Re: Question
Bonjour CyclopeEnthousiaste6670,
Je te remercie pour ta question!
Tu ne dois pas être le seul qui a besoin d'éclaircissements à ce propos, puisqu'un autre jeune nous a déjà posé cette même question, je t'invite à consulter la réponse en cliquant ici: Méthode de révision pour science secondaire 3 efficace ?? — Alloprof.
Je comprends que tu sois stressé à l’approche de ton examen de science de secondaire 3, mais il est encore temps de bien te préparer. Voici un plan d’action efficace pour t’aider à réussir :
🧠 1. Organise ta révision par thèmes
Le programme de science de secondaire 3 au Québec couvre généralement les domaines suivants :
- Univers matériel : propriétés de la matière, transformations physiques et chimiques, énergie.
- Univers vivant : cellules, systèmes du corps humain, reproduction.
- Terre et espace : phénomènes géologiques, atmosphère, système solaire.
- Univers technologique : matériaux, forces, machines simples.
Tu peux consulter le répertoire de révision d’Alloprof pour une vue d’ensemble de ces concepts.
📝 2. Utilise des outils de révision interactifs
- Cartes mentales : Crée des cartes mentales pour visualiser et relier les concepts clés. Alloprof propose un guide utile à ce sujet.
- Flashcards : Utilise des applications comme Quizlet pour mémoriser les définitions et les formules importantes.
📚 3. Pratique avec des exercices et des examens blancs
- Cahiers d’exercices : Le site Studocu offre des documents de révision avec des questions pratiques.
- Simulations d’examen : ÉtudeSecours propose des examens pratiques en ligne pour t’entraîner dans des conditions similaires à l’examen réel.
⏰ 4. Planifie ton temps de révision
- Établis un horaire : Répartis tes séances d’étude sur les jours restants avant l’examen, en consacrant plus de temps aux sujets que tu maîtrises moins.
- Fais des pauses régulières : Étudie par sessions de 25 à 30 minutes, suivies de courtes pauses pour maximiser ta concentration.
😴 5. Prends soin de toi
- Sommeil : Assure-toi de dormir suffisamment chaque nuit pour consolider ta mémoire et être en forme le jour de l’examen.
- Alimentation : Mange équilibré et reste hydraté pour maintenir ton énergie et ta concentration.
📞 6. Demande de l’aide si nécessaire
- Alloprof : N’hésite pas à poser tes questions sur le forum ou à contacter un enseignant via le service d’aide en ligne. Voici un lien qui pourrait t'aider: Répertoire de révision — Sciences — Secondaire 3 – ST | Secondaire | Alloprof
- Professeurs et camarades : Organise des sessions d’étude en groupe ou demande des éclaircissements à ton enseignant sur les points que tu ne comprends pas.
Tu as encore quelques jours pour te préparer efficacement. En suivant ces conseils et en restant motivé, tu augmenteras tes chances de réussir ton examen de science. N'hésite pas à nous réécrire si des questions persistent après ta lecture et nous t'aiderons avec plaisir!
Bon courage! 💪📘
ScorpionComique4949.
Re: Question
Bonjour JupiterIntergalactique3792,
Je vais te guider pour t'aider à trouver la réponse à ta question!
Tu poses une excellente question, et elle montre que tu réfléchis de manière critique aux concepts économiques. Il est vrai que le libéralisme économique prône une intervention minimale de l’État dans l’économie. Cependant, durant la deuxième phase de l’industrialisation au Québec (vers 1896-1929), cette idéologie a paradoxalement contribué à stimuler l’économie, notamment grâce à certaines interventions étatiques.
🏭 Le libéralisme économique et la stimulation de l’économie
Le libéralisme économique repose sur plusieurs principes fondamentaux :
- Liberté d’entreprise : les individus sont libres de créer et de gérer leurs entreprises.
- Propriété privée : les moyens de production appartiennent à des particuliers.
- Libre marché : les prix et la production sont déterminés par l’offre et la demande sans intervention de l’État.
- Concurrence : les entreprises rivalisent pour offrir les meilleurs produits au meilleur prix.
Dans ce contexte, l’État adopte un rôle facilitateur plutôt qu’interventionniste. Il crée un environnement propice au développement économique en mettant en place des infrastructures (comme les chemins de fer et les routes) et en offrant des conditions favorables aux investissements, notamment étrangers. Par exemple, le gouvernement québécois a accordé des concessions aux entreprises pour exploiter les ressources naturelles, ce qui a attiré des capitaux étrangers et stimulé la croissance industrielle.
⚖️ Une intervention étatique compatible avec le libéralisme
Bien que le libéralisme prône une intervention minimale de l’État, cela ne signifie pas une absence totale d’action gouvernementale. L’État peut intervenir de manière indirecte pour soutenir l’économie, tant que cela ne perturbe pas le libre fonctionnement du marché. Par exemple, en réduisant les barrières douanières, en offrant des subventions ou en construisant des infrastructures, l’État facilite les activités économiques sans contrôler directement la production ou les prix.
🧩 En résumé
Le libéralisme économique, en favorisant la liberté d’entreprise et la concurrence, a permis de stimuler l’économie durant la deuxième phase de l’industrialisation au Québec. L’État, tout en respectant les principes libéraux, a joué un rôle facilitateur en créant un environnement favorable aux investissements et au développement industriel. Ainsi, même avec une intervention limitée, le libéralisme a contribué à la croissance économique de cette période.
Si tu souhaites approfondir ce sujet, je te recommande la vidéo suivante qui explique en détail la deuxième phase de l’industrialisation au Canada :
la deuxième phase d'industrialisation alloprof - YouTube
N’hésite pas à me poser d’autres questions si tu as besoin de clarifications supplémentaires !
ScorpionComique4949.