Best Of
Re: Question
Merci pour ta question!
Nous comprenons très bien la tâche qui t'est demandée, mais nous préférerions que tu nous reposes ta question en y incluant tes tentatives de démarche. De cette manière, nous serons en mesure de répondre à ta question plus précisément.
N'hésite pas si tu as d'autres questions!
Re: Question
Bonsoir, DiplodocusTurbo371
En effet, la réciproque d'une fonction n'est pas toujours une fonction.
Tu dois tracer un graphique pour trouver cette information. La réciproque de f est une fonction si et seulement si aucune droite horizontale (parallèle à l'axe des x) ne coupe le graphique de la fonction f en plus d'un point.
La réciproque de cette fonction n'est pas une fonction.
N'hésite pas à poser d'autres questions!
Re: Question
Reresalut, LucioleAuthentique9488! :)
Tu trouveras l'information sur les conséquences politiques de la révolution américaine dans cette fiche:
Entre autres, c'est à ce moment où les 13 colonies anglaises deviennent un nouveau pays indépendant : les États-Unis d’Amérique. Elles se séparent de l’Angleterre et ne veulent plus être dirigées par un roi.
Bonne lecture à toi! :) À bientôt sur la Zone.
Iris
Re: Question
Salut moi je sais beaucoup de facons pour se preparer a l'examen: en avant tu lis apres tu peux
- essaye d'expliquer ce que tu as etudié a un autre personne ce que tu as de difficulté a expliquer relis .
- essaye de faire des liens entre ce que tu as appris ( exemple: probleme - solution ou conflit - cause).
- pose des questions . comme ca tu pourras comprendre mieux le theme.
- au lieu d'etudier 3 heures d'affilée etudie 20 minutes et prend une pause , etudie 20 minutes et prend une pause.
- sutout noublie pas d'aller dehors et de bien dormir . bye -Dragon Logique
Re: Question
Ça aurait été préférable de nous transmettre une photo de ton développement pour identifier ou se trouve l'erreur (dans le raisonnement ou dans le calcul).
Voici ce que j'obtiens (je peux moi-même faire des erreurs :-)
Re: Question
Bonjour FraiseRose3383,
Merci pour ta question :)
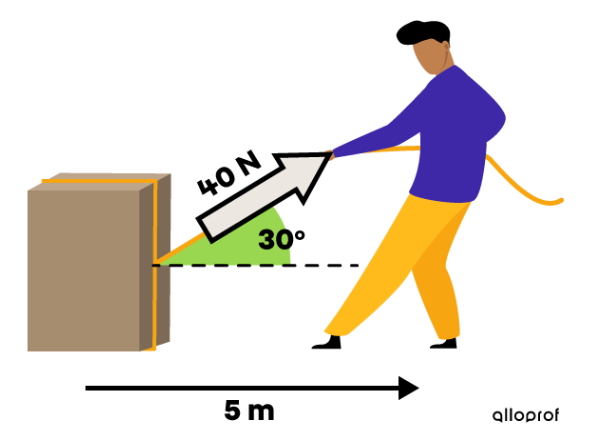
Tu as raison, dans une situation où le référentiel comprend l'axe des x horizontal et l'axe des y vertical, il est possible de calculer la plupart des composantes en x des forces avec cos et des composantes en y des forces avec sin. Voici un exemple qui s'inscrit dans cette situation:
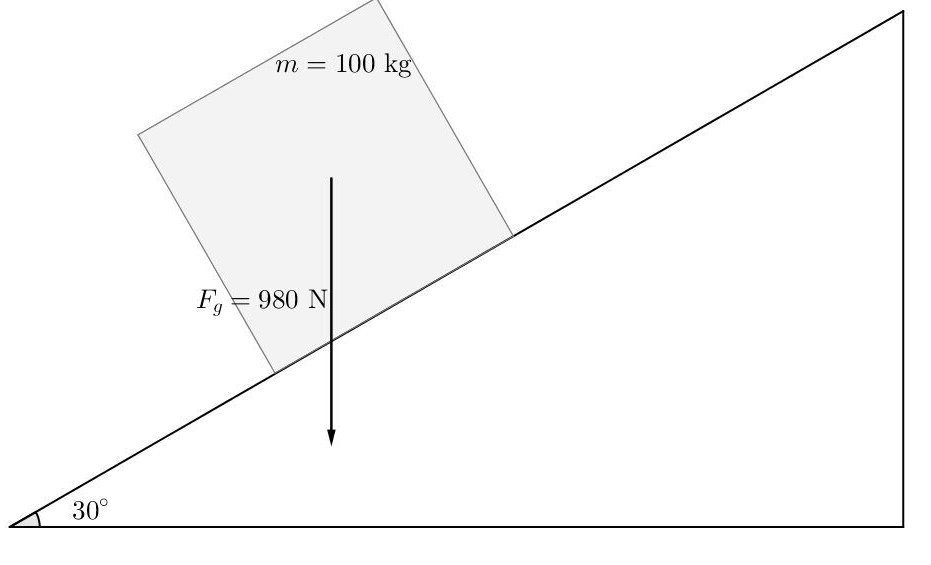
La composante en x se calculera avec un cos. Cependant, voici un exemple où il faut calculer les composantes de la force gravitationnelle d'un autre façon:
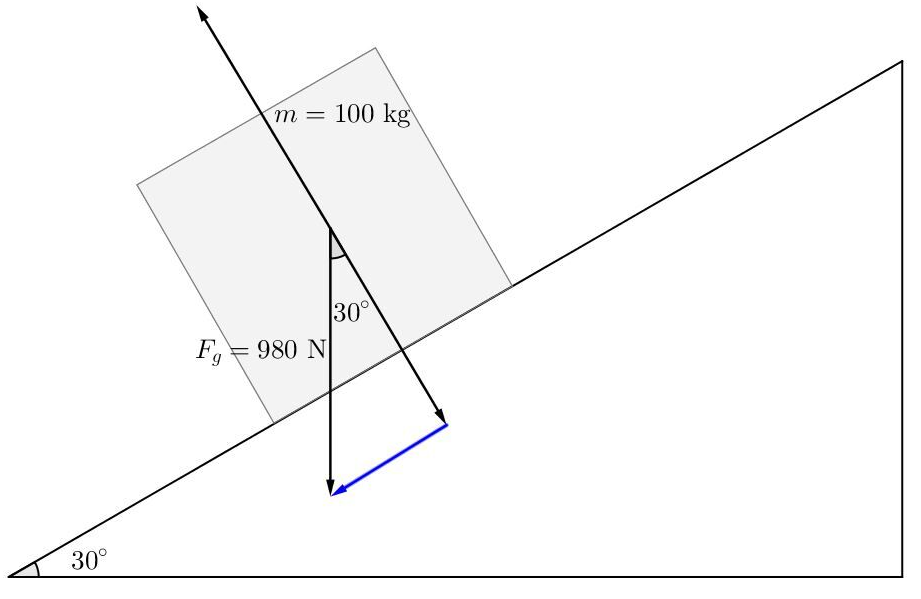
Dans cet exemple, on voit que la force gravitationnelle est vers le bas, mais que le plan incliné est orienté à 30 degrés. Notre système de référence sera donc orienté aussi à 30 degrés. On peut donc séparer la force gravitationnelle en ses deux composantes (la flèche bleue qui est la composante en x et la flèche noire vers la surface du plan incliné est la composante en y):
Comme tu peux le voir, le calcul des composantes ici dépend du triangle formé par la force gravitationnelle, sa composante en x et sa composante en y. En raison des rapports trigonométriques dans ce triangles, il faudrait effectivement calculer la composante en x avec un sin. Cela m'amène à te dire que même si la plupart des exercices se font dans des référentiels « normaux », il vaut toujours mieux faire un schéma de la situation et utiliser les rapports trigonométriques pour faire les calculs des composantes, puisque le calcul peut varier d'un problème à l'autre.
Pour ton autre question, une force résultante est équivalente à l'ensemble des forces appliquées sur l'objet. C'est l'équivalent de remplacer toutes les forces qui s'appliquent sur un objet par une seule qui prend en compte leurs effets respectifs. Pour déterminer la force résultante, il faut tenir compte de l'intensité des forces en présence, du sens et de l'orientation de ces forces.
Un système qui subit une force résultante non nulle sera en mouvement, puisque selon la seconde loi de Newton, F=ma. Or, si l'on veut que l'objet reste immobile, il faut que la somme des forces soit nulle (dans la composante x comme y). La force équilibrante est donc la force qui est d'égale grandeur et de sens opposé à la force résultante pour que la somme des forces soit 0. Par exemple, si la force résultante sur un objet a les composantes (-3 N, 6N), la force équilibrante aura comme composantes (3 N, -6 N). Ainsi, en faisant le bilan des forces en x on obtient 0 (-3+3=0, et en faisant le bilan des forces en y on obtient 0 (6-6=0).
N'hésite pas si tu as d'autres questions :)
Sandrine
Re: Question
Bonsoir, FraiseTurquoise2087!
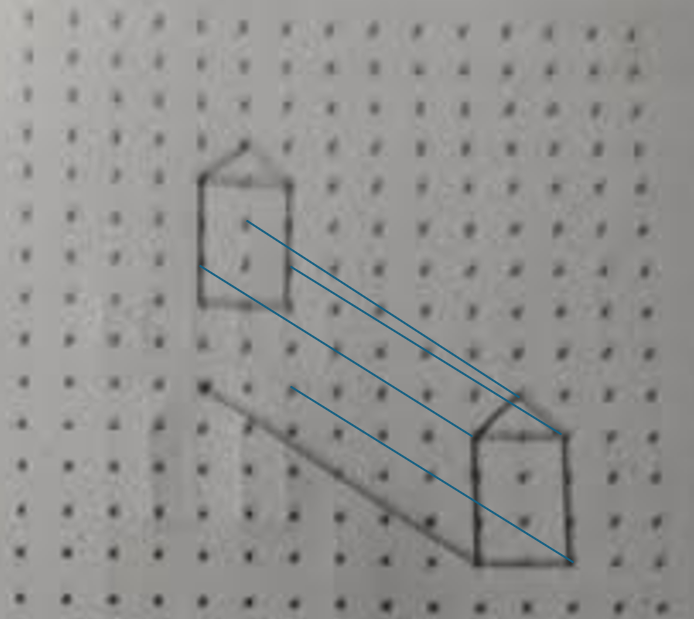
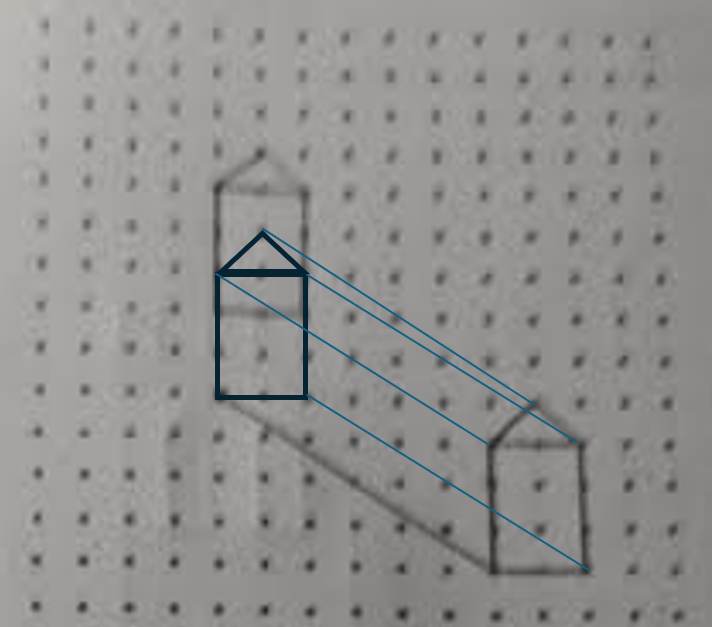
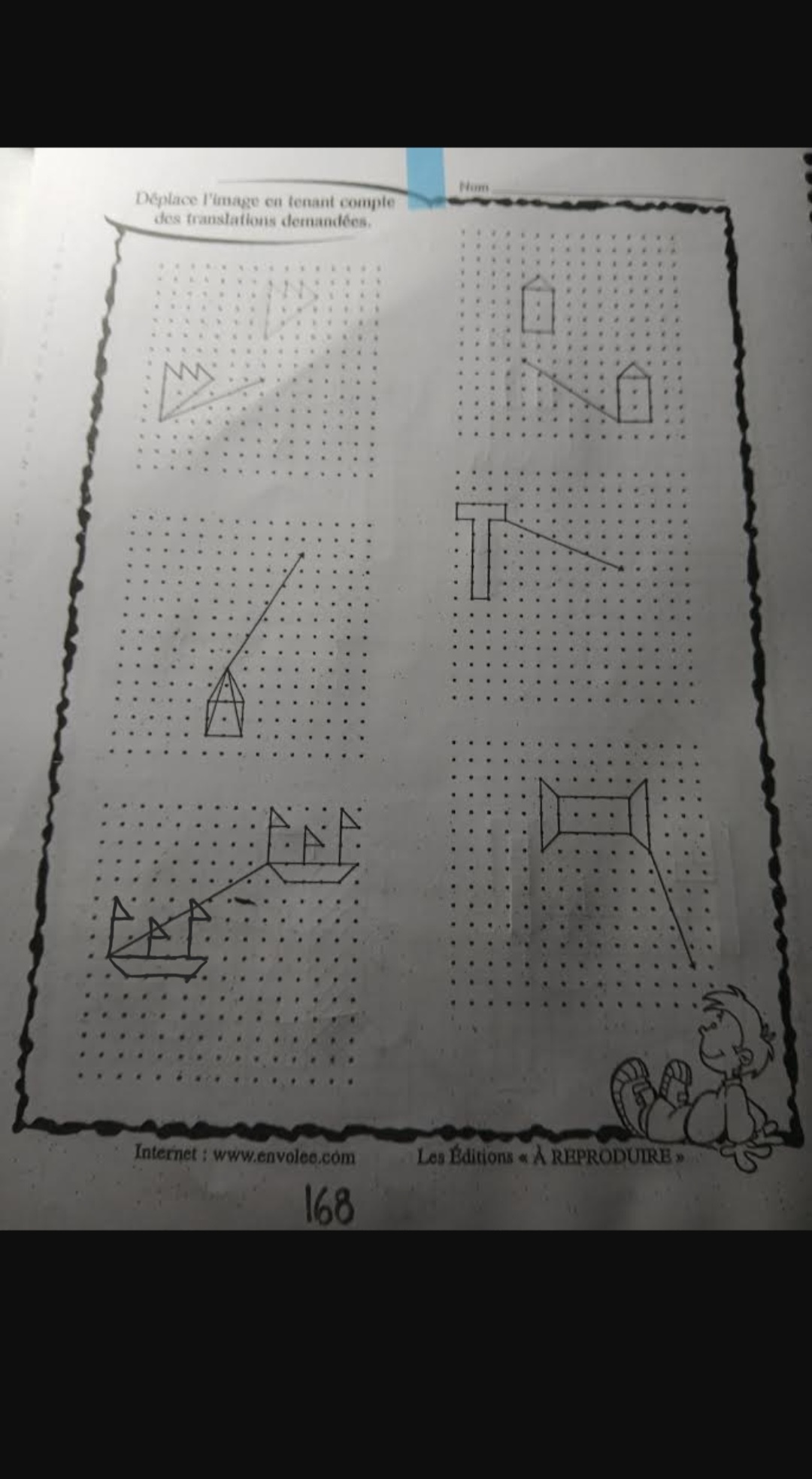
Comme DiplodocusTurbo371 l'a mentionné, il faut que tu retranscrives le dessin exactement à l'endroit où la flèche pointe. Ainsi, le dessin doit être collé à la flèche. Donc, tes deux premières traces ne sont pas bonnes.
Puisque la ligne part de la base gauche de la maison, tu n'as qu'à retracer ainsi.
En cas de doute, dis toi que si la ligne traverse 6 unités vers la gauche et 4 vers le haut, chaque point de la figure doit suivre ce mouvement également.
Tu obtiens ainsi le résultat suivant.
N'hésite pas à poser d'autres questions!
Re: Question
Bonsoir, RubisOptimiste8560!
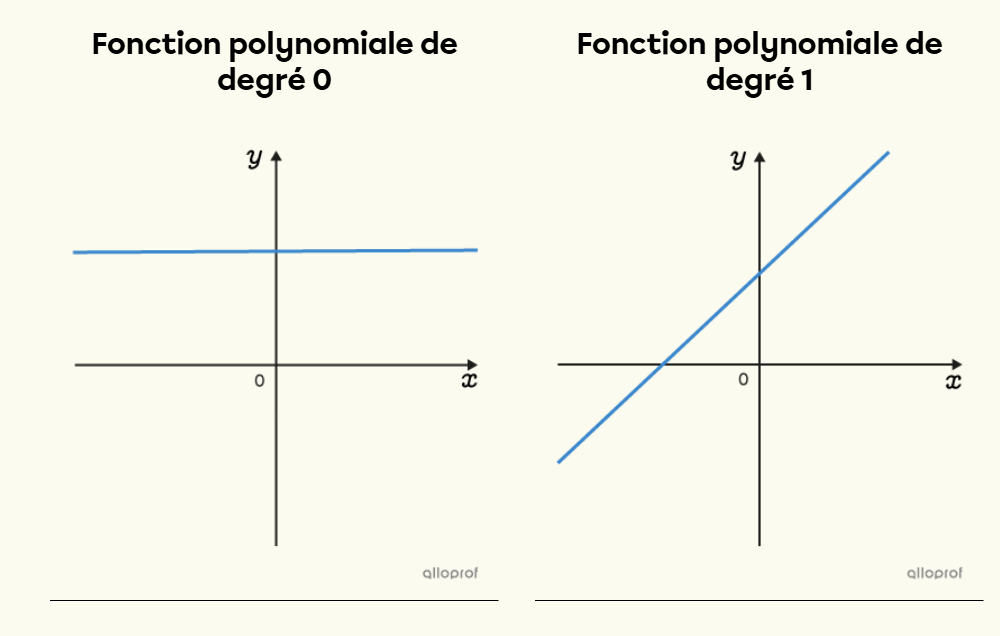
Une fonction affine est une fonction dont le taux de variation est constant.
Sa règle s'écrit sous la forme f(x)=ax+b. Graphiquement, une fonction affine est représentée par une droite.
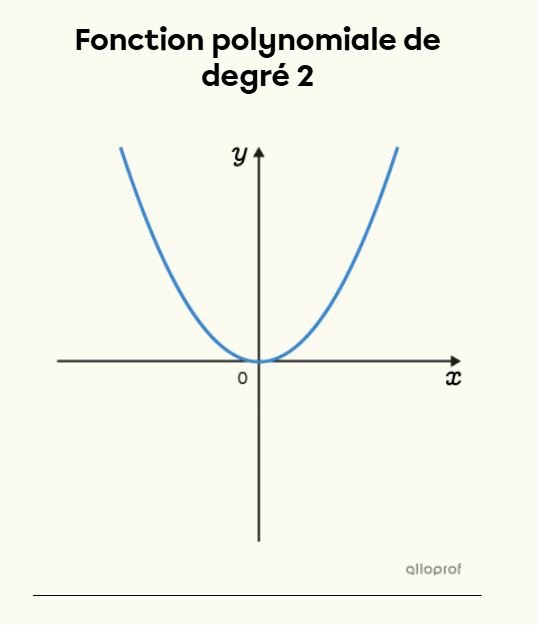
Une fonction polynomiale de degré 2 est définie par un polynôme de la forme ax²+bx+c.
Dans un plan cartésien, une fonction polynomiale de degré 2 est représentée par une parabole.
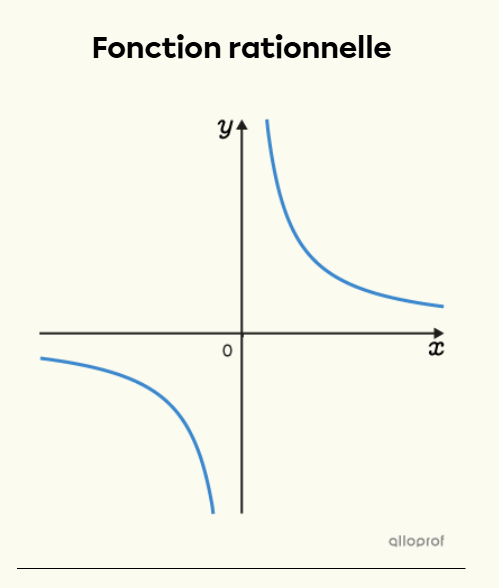
Les fonctions rationnelles regroupent toutes les fonctions où l’on retrouve une fraction dans laquelle la variable indépendante (x) est au dénominateur.
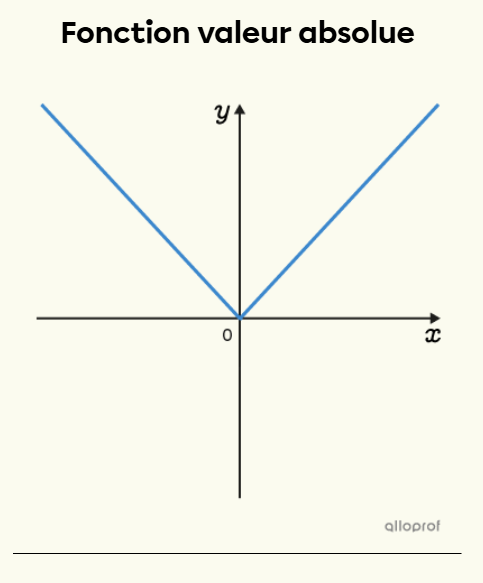
La forme de base pour une fonction valeur absolue est : f(x)=∣x∣.
Elle est représentée par deux droites que l'on appelle branches.
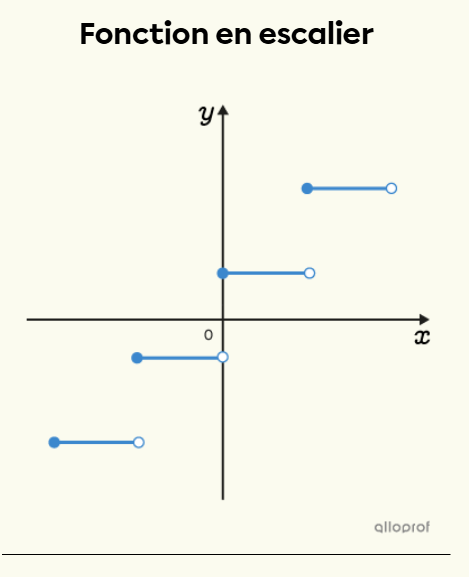
On appelle fonction en escalier une fonction qui est constante sur des intervalles.
Elle est formée de plateaux qui sont appelés marches et la distance entre les plateaux est appelée contremarche.
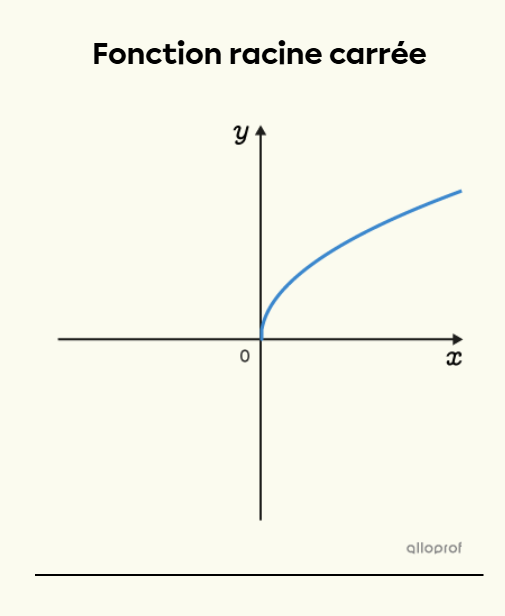
L'équation de la fonction racine carrée peut s'écrire f(x)=a√(bx).
Sous cette forme, on remarque qu'il y a un sommet et qu'il se situe toujours à l'origine (0,0).
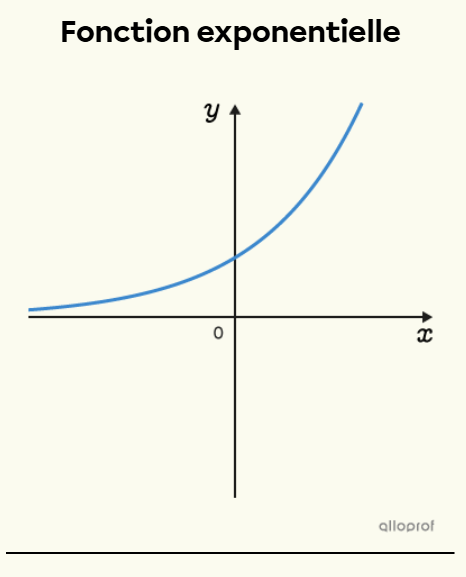
La famille des fonctions exponentielles regroupe les fonctions pour lesquelles la variable indépendante (x) est un exposant.
Toutes les fonctions exponentielles possèdent une asymptote. Graphiquement, cela signifie que les fonctions exponentielles sont représentées par une courbe qui se rapproche d’une droite horizontale sans jamais la croiser.
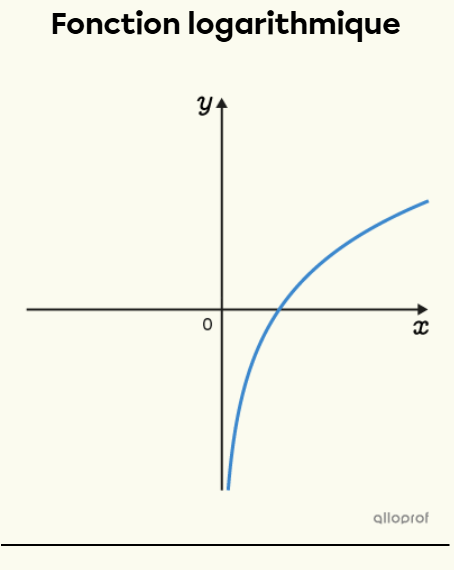
La fonction logarithmique est la réciproque de la fonction exponentielle. C’est une fonction qui comporte une asymptote verticale et dont le domaine est restreint.
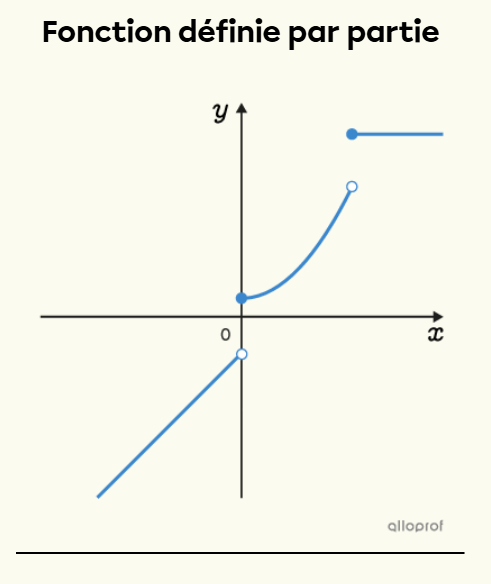
Une fonction définie par parties est une fonction dont la règle diffère selon l'intervalle où se situe la variable x.
Comme son nom le mentionne, la fonction définie par parties est composée de plusieurs parties.
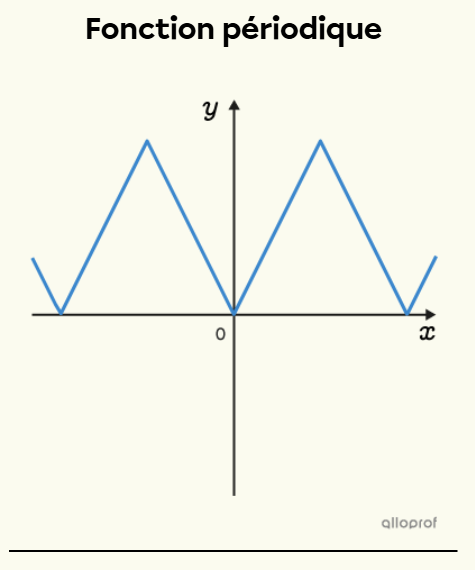
Graphiquement, les fonctions périodiques font référence à un modèle qui est reproduit à plusieurs reprises dans le plan cartésien.
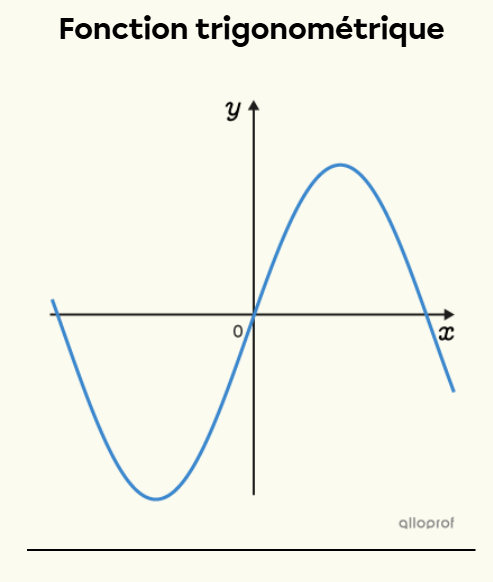
L'expression fonction trigonométrique est un terme général utilisé afin de désigner, entre autres, l'une ou l'autre des fonctions suivantes: sinus, cosinus, tangente, sécante, cosécante, cotangente. On appelle aussi ces fonctions des fonctions circulaires. Aussi, les fonctions trigonométriques sont d'excellents exemples de fonctions périodiques.
Les fonctions trigonométriques sont des fonctions périodiques. Une fonction f(x) est périodique s'il existe un nombre positif P (la période) tel que f(x±P)=f(x) pour toutes les valeurs de x dans le domaine de la fonction.
N'hésite pas à poser d'autres questions!
Re: Question
Salut!
Je ne suis pas prof, mais jai déjà vu ça en maths, c'est super simple ! Il faut simplement que tu retranscrive le dessin exactement à l'endroit ou la flèche pointe, et tu doit vraiment tracer le meme trait ou la flèche touche le premier dessin, comme ceci avec le bateau
Re: Question
Bonjour TortueOrange9884,
Merci de faire appel à la Zone d'entraide!
Vous trouverez ci-dessous une synthèse de stratégies éprouvées pour dépasser les 70 % à votre prochain examen, réparties en trois phases clés : avant, pendant et après l’épreuve.
Avant l’examen
1. Planifier et répartir les révisions
- Évitez le bachotage de dernière minute : étudiez plusieurs jours à l’avance en petites sessions (20–30 min), plutôt qu’une longue séance la veille.
- Utilisez un agenda ou un planning d’étude pour noter devoirs, leçons et dates d’examens. Cela vous aide à visualiser l’ensemble des tâches à accomplir et à répartir équitablement vos révisions.
2. Travailler activement le contenu
- Relisez vos notes quotidiennement : prenez le temps de revoir chaque soir les nouveautés apprises en classe pour consolider la mémoire à long terme.
- Créez des fiches synthèses ou des cartes mémoire (flashcards) pour les définitions, formules et dates clés.
- Codez vos fiches avec des couleurs pour repérer rapidement les thèmes (définitions en bleu, formules en rouge, exemples en vert, etc.).
3. Préparer le corps et l’esprit
- Bien manger avant l’examen : un petit-déjeuner équilibré ou une barre protéinée favorise la concentration.
- Dormez suffisamment : un sommeil réparateur réduit la fatigue mentale et le stress le jour J.
- Discutez avec vos pairs ou posez des questions à l’enseignant pour éclaircir les points flous, plutôt que de rester bloqué seul.
Pendant l’examen
1. Gérer son temps
- Survolez rapidement toutes les questions pour avoir une vue d’ensemble et repérer celles que vous maîtrisez en premier.
- Allouez un temps précis par question : par exemple 5–10 min pour une question courte, 20–30 min pour un problème plus long, puis revenez aux points non traités.
2. Adopter une démarche méthodique
- Relisez chaque énoncé au moins deux fois, surlignez les mots-clés et reformulez le problème dans vos propres mots.
- Laissez des traces de votre raisonnement : montrez toutes les étapes, même en cas d’erreur partielle, pour obtenir un maximum de points.
3. Gérer le stress
- Respirez profondément avant et pendant l’épreuve : inspirez lentement en comptant jusqu’à 4, puis expirez en relâchant les épaules.
- Ne vous mettez pas trop de pression : rappelez-vous que vous avez bien révisé et que l’erreur est humaine. Un petit moment de calme suffit souvent à repartir du bon pied.
Après l’examen
1. Autoévaluer pour progresser
- Corrigez-vous en comparant vos réponses au corrigé pour identifier vos points forts et faiblesses. Notez les erreurs récurrentes pour y remédier la prochaine fois.
- Planifiez une séance de rattrapage sur les concepts mal compris : refaites des exercices ou interrogez l’enseignant sur les points obscurs.
2. Maintenir de bonnes habitudes
- Étudiez régulièrement même hors période d’examen pour conserver un rythme de travail constant et réduire la pression de dernière minute.
- Entourez-vous de soutien : regroupez-vous en petits groupes d’étude, échangez des astuces et encouragez-vous mutuellement.
En appliquant ces conseils de manière rigoureuse et progressive, vous créerez un cercle vertueux : plus vous étudierez efficacement, moins le stress vous affectera, et mieux vous retiendrez la matière. Voici quelques liens Alloprof qui pourront vous aider:
Trucs pour mieux étudier | Alloprof
Étudier plus efficacement : des techniques amusantes pour réussir ton prochain examen! | Alloprof
Adapter sa façon d'étudier à sa capacité de concentration | Alloprof
Bon succès pour votre prochain examen!
ScorpionComique4949.