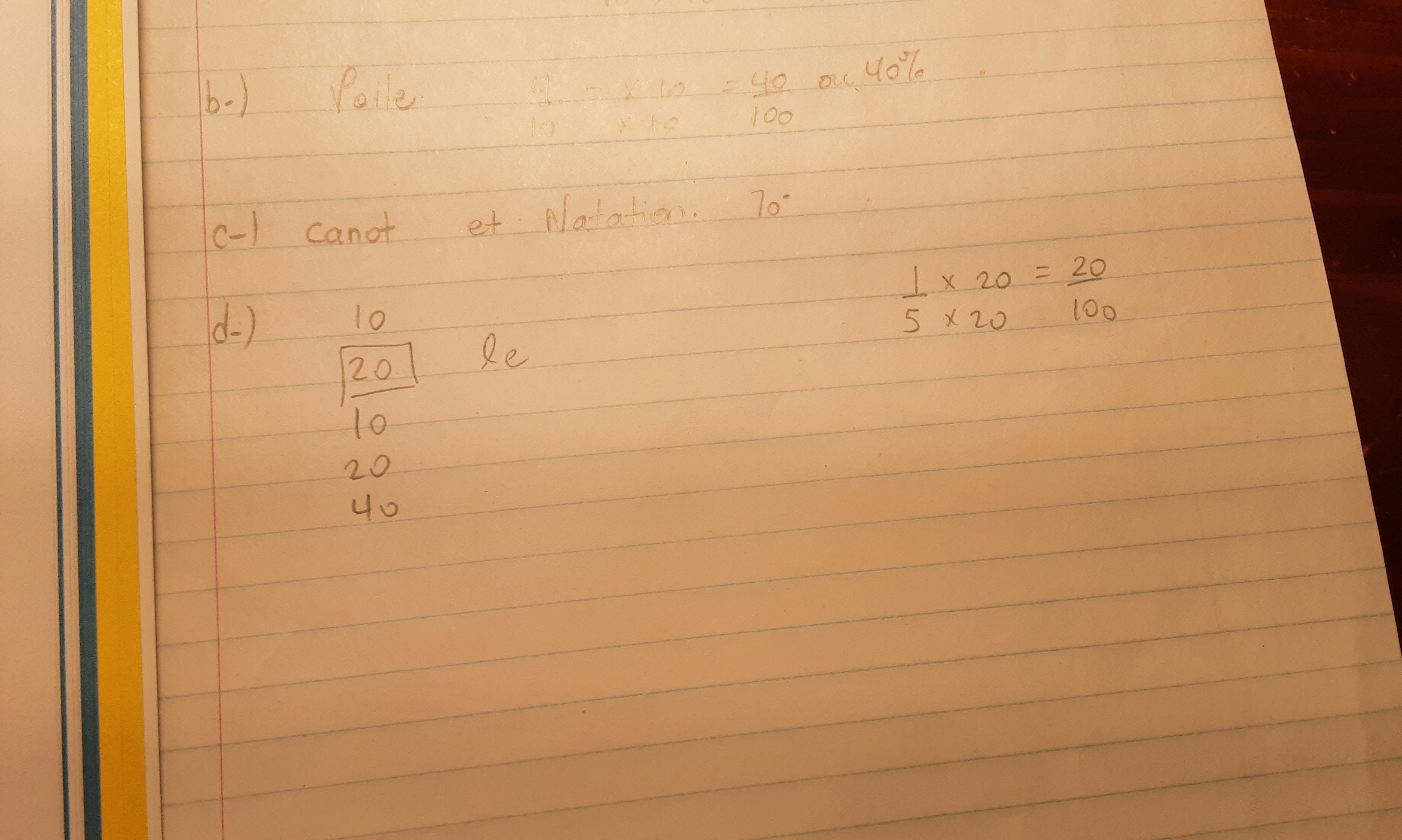Best Of
Re: Question
Quand à moi l'important et de résoudre le problème. Utilise la forme qui te permet de faire cela le plus facilement possible.
En a) multiplie l'inéquation par 25 (des deux côtés pour préserver l'inégalité) et pour te débarrasser des fractions
x² - 7x + 316 >48·25
ensuite place tous tes termes du même côté de l'inégalité (n'oublie pas que si tu multiplies une inéquation par un nombre négatif, tu dois changer le sens de l'inéquation)
ensuite trouve les zéros de cette parabole et détermine l'intervalle pour lequel la parabole est dans ce cas particulier au dessus de zéro (>0) en utilisant
En b) commence par multiplier tous les termes et les mettre du même côté de l'inégalité.
Re: Question
Bonjour QuartzNoble9608
Voici une vidéo où on présente quatre fonctions quadratiques sous différentes formes. Vous y trouverez plusieurs exemples de conversion d'une forme à une autre. J'espère que cela vous aidera à consolider vos connaissances.
Re: Question
Salut!
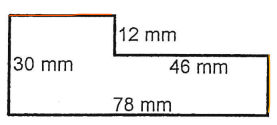
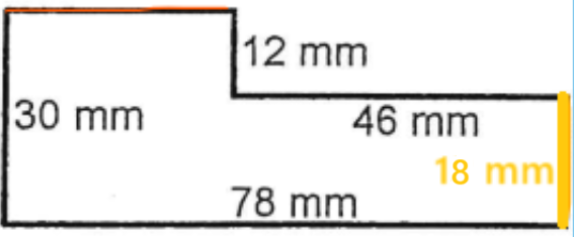
Quand tu cherches une mesure manquante dans ce genre de figure :
Essaie toujours de sélectionner des segments qui te permettront de former une ligne droite complète.
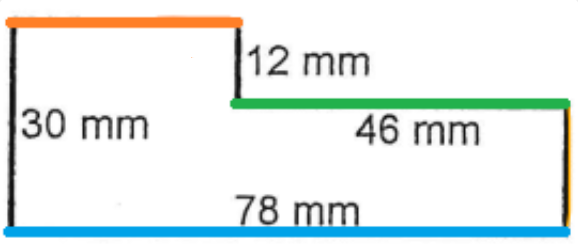
Ici, pour trouver la mesure manquante du haut (en orange), on peut voir qu'en la combinant au segment vert, on obtient une ligne droite complète qui est de la même longueur que le segment bleu :
$$ {\color{Orange} segment~ orange} + {\color{Green} segment~ vert} = {\color{Blue} segment ~ bleu} $$
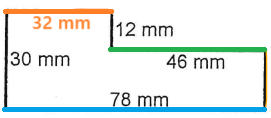
Ainsi, notre segment orange est une petite partie du segment bleu. En d'autres mots, notre segment bleu est composé de deux parties : le segment vert et le segment orange.
$$ {\color{Orange} segment~ orange} = {\color{Blue} 78 ~ mm} - {\color{Green} 46~ mm} = {\color{Orange} 32~ mm} $$
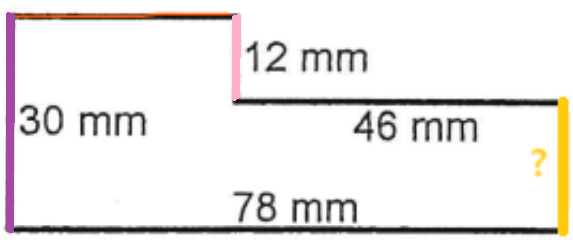
C'est la même chose si on veut trouver l'autre mesure manquante (en jaune) :
On voit que :
$${\color{Purple} segment~mauve}={\color{Pink} segment~rose}+{\color{Yellow} segment~jaune}$$
En combinant notre droite rose et notre droite jaune, on obtiendrait une droite de la même mesure que la droite mauve! Donc, pour trouver la mesure manquante, on effectue ce calcul :
$${\color{Purple} 30~mm}-{\color{Pink} 12~mm}={\color{Yellow} 18~mm}$$
Est-ce que c'est plus clair? Si tu as encore des doutes, dis-le-nous! Mais, explique-nous un peu ton point de vue pour que je puisse être en mesure de mieux t'aider: qu'est-ce qui te cause un doute exactement? Est-ce que tu n'arrives pas à visualiser? Et toi, qu'aurais-tu fait pour trouver les mesures manquantes? Quelles mesures toi tu aurais soustraites pour trouver le segment horizontal orange inconnu? Pourquoi aurais-tu fait ça? Et qu'en est-il du segment jaune vertical, comment aurais-tu procédé pour le trouver?
Ainsi, si tu as encore de la difficulté, réécris-nous, mais détaille nous un peu plus tes doutes, cela m'aidera à mieux comprendre tes difficultés et ainsi mieux y répondre :)
Re: Question
Salut CoccinelleAdorable4413,
Donc , tu dois d'abord savoir c'est quoi un mélange homogène.
Une mélange homogène qui est composée de deux substance qu'on ne peut pas distinguer à l'oeil nu.
Un mélange homogène n'a donc Qu'une seul phase visible.
Une melange héterogene, elle, est composé de deux ou plusieurs substances qu'on peut distinguer à l'oeil nu.
Une mélange hétérogène a donc plusieurs phases visible.
Maintenant passant a une solution.
Alors une solution c'est un mélange homogène dans lequel une ou plusieurs substances sont dissoutes dans une autre substance.
C'est la soluté et le solvant
Dans une solution, la substance solide, liquide ou gazeuse est le solute.
Le soluté est la substance généralement présente en plus petite quantité dans la solution.
Maintenant passant au solvant.
La substance solide,liquide ou gazeuse dans laquelle le soluté est dissout est le solvant.
Le solvant est généralement présente en plus grande partie.
J'espère que maintenant tu as compris ton cours.
Bonne journée
Re: Question
Salut!
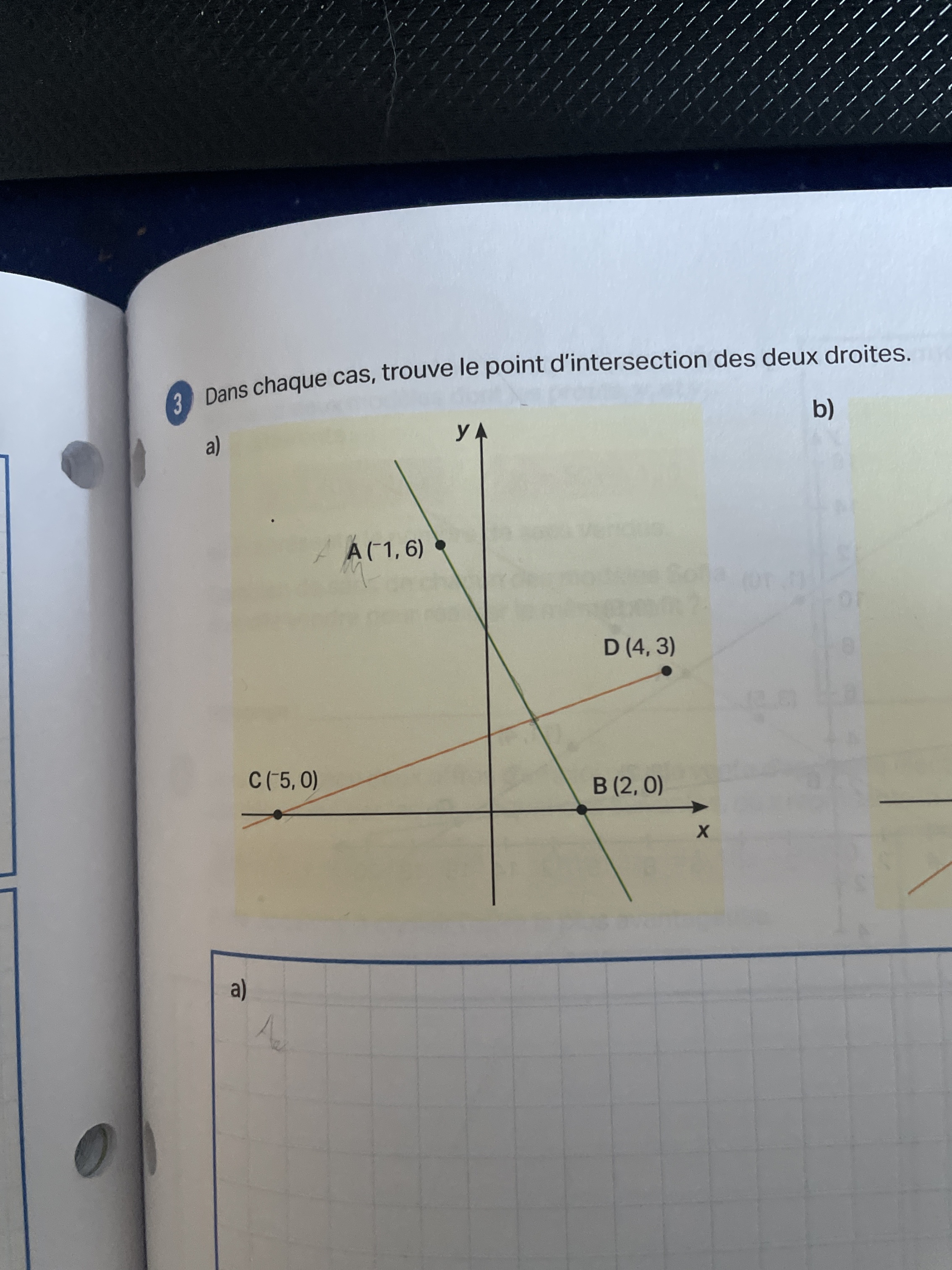
La première étape dans cet exercice sera de trouver l'équation des deux droites. Pour cela, tu peux utiliser les points donnés. Tu dois suivre ces étapes pour trouver l'équation de la droite AB et l'équation de la droite CD :
Consulte ceci au besoin : Trouver la règle d'une fonction affine | Secondaire | Alloprof
Ensuite, pour trouver le point d'intersection de deux droites, c'est-à-dire les coordonnées (x, y) du point où les deux droites se croiseront, où elles se toucheront, on doit résoudre un système d'équations.
Je te donne un exemple similaire où on a terminé la première étape et on connait maintenant l'équation des deux droites :
Pour trouver le point d'intersection de la droite bleue et de la droite mauve (le point rouge ?), tu dois utiliser la méthode de comparaison pour résoudre ce système d'équations. Nous avons :
$$\left\{\begin{matrix} y_{1}=\frac{1}{2}x+3 \\y_{2}=-x-3 \end{matrix}\right. $$
On cherche un point tel que \((x_{1},y_{1}) = (x_{2}. y_{2})\). On commence par former une équation à une variable en comparant les deux règles :
$$ y_{1} = y_{2}$$
$$\frac{1}{2}x+3 = -x-3$$
On peut maintenant résoudre cette équation à une variable.
On place les termes semblables du même côté de l'équation :
$$\frac{1}{2}x+3 +x= -x-3+x$$
$$(\frac{1}{2}+1)x+3 = -3$$
$$(\frac{1}{2}+\frac{2}{2})x+3 = -3$$
$$\frac{3}{2}x+3 = -3$$
On déplace la constante 3 de l'autre côté de l'équation :
$$\frac{3}{2}x+3-3 = -3-3$$
$$\frac{3}{2}x= -6$$
On élimine le coefficient de la variable x :
$$\frac{3}{2}x \div \frac{3}{2}= -6\div \frac{3}{2}$$
$$x= -6\div \frac{3}{2}$$
$$x= -6\times \frac{2}{3}$$
$$x= \frac{-6\times2}{3}$$
$$x= \frac{-12}{3}$$
$$x= -4$$
Nous avons ainsi trouvé la coordonnée en x du point d'intersection des deux droites. Il nous reste maintenant à trouver la coordonnée en y. Pour cela, on peut utiliser l'une des deux équations de notre système (n'importe laquelle, le résultat sera le même), et calculer y pour x=-4.
$$y=\frac{1}{2}x+3 $$
$$y=\frac{1}{2}(-4)+3 $$
$$y=\frac{-4}{2}+3=-2+3=1$$
ou
$$y=-x-3$$
$$y=-(-4)-3=4-3=1$$
Voilà! Le couple solution de ce système est donc (-4, 1).
Voici une fiche sur cette notion qui pourrait t'être utile : La résolution de systèmes d'équations linéaires | Secondaire | Alloprof
Dans ton exercice, tu peux suivre la même démarche pour trouver le point d'intersection!
Je te laisse essayer avec ces indices. J'espère que c'est plus clair pour toi! :)
Question
Bonjour Sandrine et Katia,
On me demande quelle activité an singulier le 1/5 des jeunes préfère?
- 1/5 est égal à 20/100
Donc j'aurais le canot et la natation?
Re: Question
Salut!
Si sa peut t'aider, les mélanges est une association de plusieurs substance qui ne provoquent pas de réactions chimique entre elles
Re: Question
Salut!
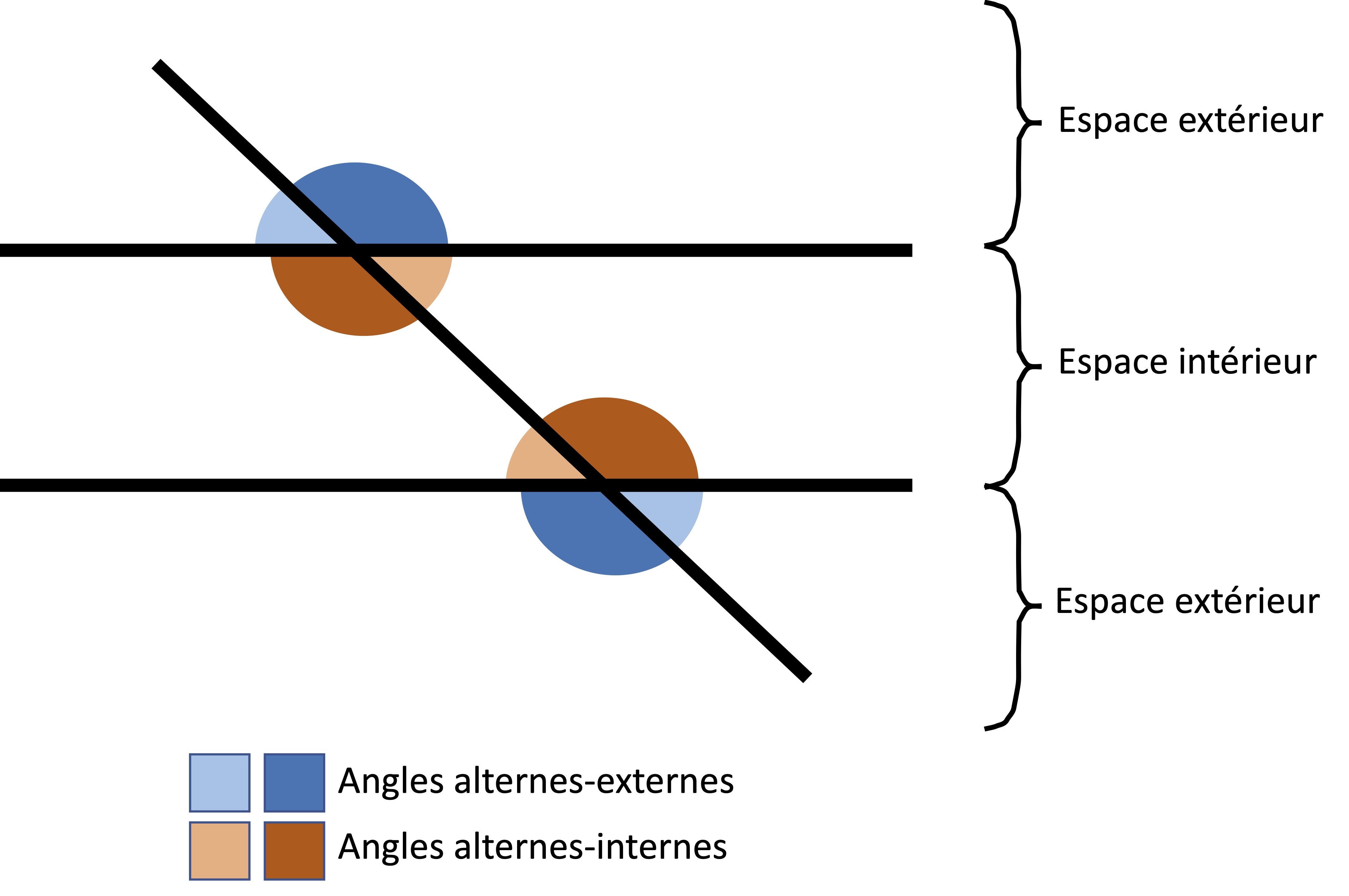
Les angles alternes-internes et les angles alternes-externes sont formés par une droite sécante coupant deux droites parallèles. Ces angles sont situés de part et d'autre de cette droite sécante (un angle à gauche de la droite sécante, et l'autre à droite).
La différence est que les angles alternes-internes sont dans l'espace à l'intérieur des droites parallèles, ils sont donc dans l'espace interne, tandis que les angles alternes-externes sont situés dans l'espace à l'extérieur des droites parallèles, dans l'espace externe.
En bref, alternes-internes = à l'intérieur des droites, alternes-externes = à l'extérieur des droites.
Voici une fiche sur cette notion qui pourrait t'être utile : Les relations entre les angles | Secondaire | Alloprof
Si tu as d'autres questions, on est là! :)