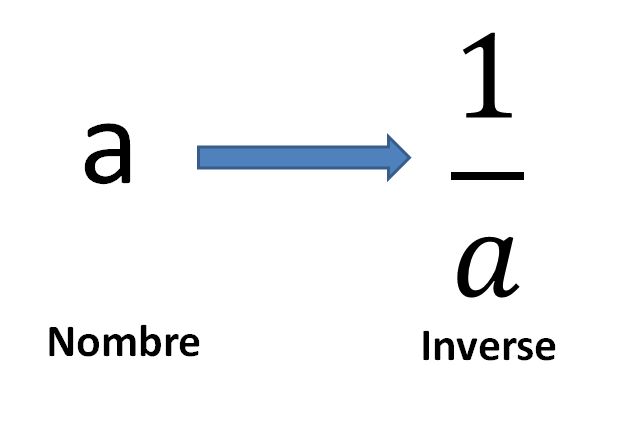Best Of

Bonjour

merci pour votre réponse! Est ce que c’est possible que dans les examens ( surtout du ministère) il y a des grandes résolutions de problèmes ou on doit appliquer géométrie + algèbre+statistique etc tout dans la même résolution?

quels sont les type de combinaisons fréquentes?

merci beaucoup!

Salut!

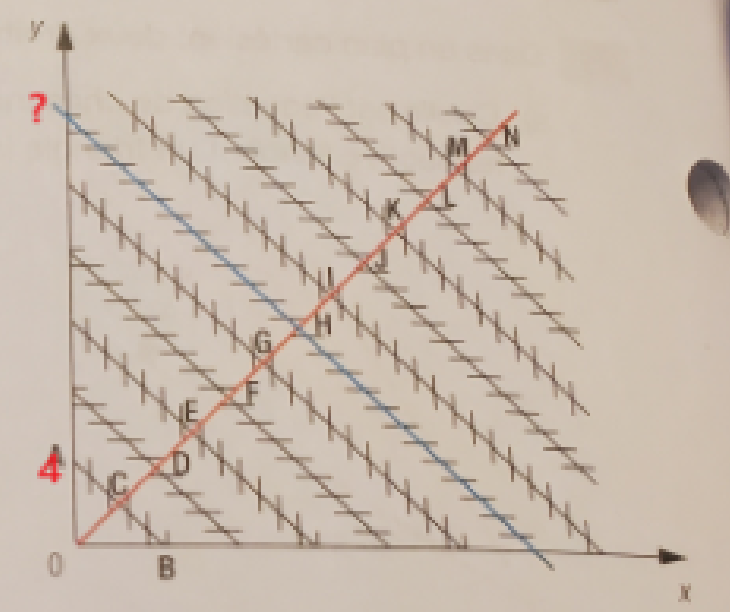
On sait que toutes les droites (sauf la droite orange) sont parallèles, donc elles ont la même pente. L’équation de la droite AB est \(x+y-4=0\). On peut la réécrire sous la forme canonique, ce qui nous donne \(y=−x+4\), donc nous avons une pente de −1.

On veut trouver l’équation de la droite bleue qui est parallèle à la droite AB. Donc, elle aura la même pente que la droite AB, soit de −1. Son équation sera donc :

$$y=-x+b$$

où \(b\) est son ordonnée à l'origine à déterminer.

On doit maintenant déterminer cette valeur de \(b\).

Ce contenu est protégé par le droit d'auteur. Toute reproduction à l'extérieur des forums Alloprof est interdite et pourra être considérée comme une violation du droit d'auteur.

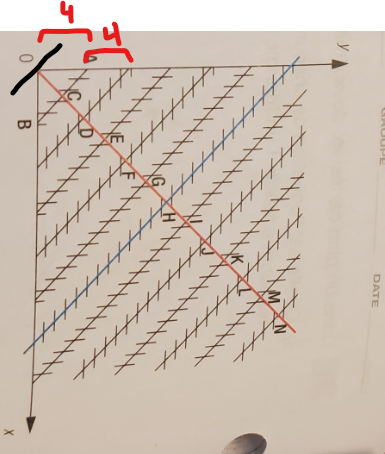
Puisqu'il n'y a aucun point de repère donné dans le graphique, il faudra y aller par estimation. La droite AB a une ordonnée à l'origine de 4. Si on estime qu'on a une droite parallèle à AB à l'origine du graphique, cela signifierait que les droites parallèles sont toutes à une distance de 4.

Ce contenu est protégé par le droit d'auteur. Toute reproduction à l'extérieur des forums Alloprof est interdite et pourra être considérée comme une violation du droit d'auteur.

Sachant cela, tu peux trouver l'ordonnée à l'origine de la droite bleue.

Cela dit, je te conseillerais de vérifier auprès de ton professeur s'il ne manque pas de l'information ou s'il n'y a pas une erreur dans l'énoncé. La démarche que je te propose n'est pas la plus rigoureuse, puisqu'il se pourrait que la droite parallèle à AB qui la précède ne passe pas par l'origine. Par exemple, elle pourrait passer par y=-1, ce qui signifierait que la distance entre les droites parallèles équidistante est de 5 (de y=-1 à y=4, on a un déplacement de 5 unités). Malheureusement, puisque nous n'avons aucun repère dans le graphique (aucun point donné, aucune graduation), alors il est simplement impossible d'en être sûr, et l'estimation est la seule méthode qu'il nous reste.

J'espère que cela t'aide malgré tout! :)

PS Pourrais-tu envoyer tes photos pour qu'elles soient horizontales les prochaines fois stp? C'est plus facile à lire pour nous 😋.

Salut!

Deux droites perpendiculaires ont des pentes opposées et inverses.

Ce contenu est protégé par le droit d'auteur. Toute reproduction à l'extérieur des forums Alloprof est interdite et pourra être considérée comme une violation du droit d'auteur.

Ce contenu est protégé par le droit d'auteur. Toute reproduction à l'extérieur des forums Alloprof est interdite et pourra être considérée comme une violation du droit d'auteur.

Par exemple, si une droite a une pente de 4, alors la pente d'une droite qui lui est perpendiculaire sera de -1/4. Autre exemple, si une droite a une pente de -1/9, alors la pente de la droite perpendiculaire est de 9.

Voici une fiche sur cette notion pour plus d'exemples : L'équation de droites parallèles ou perpendiculaires | Secondaire | Alloprof

Cela dit, dans ton exercice, tu as des droites particulières. Tu as des droites horizontales :

Ce contenu est protégé par le droit d'auteur. Toute reproduction à l'extérieur des forums Alloprof est interdite et pourra être considérée comme une violation du droit d'auteur.

ou verticales :

Ce contenu est protégé par le droit d'auteur. Toute reproduction à l'extérieur des forums Alloprof est interdite et pourra être considérée comme une violation du droit d'auteur.

Ainsi, si tu as une droite horizontale, les droites qui lui seront perpendiculaires seront verticales. Par exemple, x=1, x=-1, x=5 sont des exemples de droites perpendiculaires à y=5.

À l'inverse, si tu as une droite verticale, les droites qui lui seront perpendiculaires seront horizontales. Par exemple, y=1, y=-1, y=5 sont des exemples de droites perpendiculaires à x=5.

Je te laisse compléter ton exercice. J'espère que c'est plus clair pour toi! Réécris-nous si tu souhaites vérifier tes réponses :)

Salut!

Il n'y a pas de règle précise, mais on décide habituellement d'arrondir les nombres à la position qui a le plus de sens selon le contexte.

Par exemple, si on cherche le cout de construction d’une maison et que la plupart des items à considérer dans le prix sont dans les unités de mille ou les dizaines de mille, on s’attend à trouver un cout total dans les dizaines de mille ou les centaines de mille. Si l’approximation du calcul qu’on s’apprête à faire donne une réponse beaucoup plus petite ou beaucoup plus grande, on a probablement commis une erreur.

Pour ton exemple : 38 684 + 779 + 2874 + 412, ça dépend du niveau de précision que tu veux. Si tu veux une estimation rapide, tu pourrais arrondir aux unités de mille près :

• 38 684 devient environ 39 000
• 779 devient environ 800
• 2874 devient environ 3000
• 412 devient environ 400

Ensuite, tu additionnes : 39 000 + 800 + 3000 + 400 ≈ 43 200.

Si tu veux être encore plus rapide (donc moins précis), tu pourrais arrondir aux dizaines de mille près :

• 38 684 devient environ 40 000
• 779 devient environ 1000
• 2874 devient environ 3000
• 412 devient environ 0 (ou 500 si tu veux garder une approximation)

En additionnant : 40 000 + 1000 + 3000 + 500 ≈ 44 500.

L’important, c’est de choisir un niveau d’arrondissement qui te permet d’estimer rapidement tout en restant assez proche de la vraie réponse. N’hésite pas à ajuster selon ce qui est demandé ou selon le contexte!

Voici des fiches qui pourraient t'être utiles :

• L'approximation du résultat d'une opération | Secondaire | Alloprof
• L'approximation et l'arrondissement d'un nombre | Secondaire | Alloprof

J'espère que c'est plus clair pour toi! N’hésite pas si tu as d’autres questions! 🙂