Best Of
Re: Question
Bonjour, GeckoAgile3866!
Merci pour ta question.
Oui, tu peux mettre ces mots en guillemets pour signaler qu’ils sont empruntés à l’anglais. Cependant, cela ne garantit pas qu’ils seront acceptés sans être considérés comme des fautes. Pour être certain, je poserais cette question à un professeur de ton école.
Sinon, si tu désires être sûr de ne pas être pénalisé, je remplacerais certains mots par d'autres :
« Cool » par branché, populaire, tendance...
« Awkward » par maladroit, gênant, embarrassant...
Et « Chill » par détendu, tranquille.
Si ça t'intéresse, voici les critères de correction de cet examen:
Enfin, voici une fiche avec d'autres informations sur l'épreuve :
Voilà, j'espère avoir répondu à ta question.
N'hésite pas si tu en as d'autres.
Iris :)
Re: Question
Bonsoir, TritonAimable2010!
Sur la fiche suivante, tu peux voir le type de questions qui sont posées à l'examen du ministère de la sixième année.
Tu peux parcourir notre répertoire de révision et faire les exercices associés aux notions dont tu as besoin de réviser.
Votre enseignant va sûrement vous donner des pratiques. Tu peux également acheter des cahiers de préparation dans des librairies ou des papeteries.
N'hésite pas à poser d'autres questions!
Re: Question
Si je retournerais au primaire ou même dans mes années plus jeune le conseil que je me donnerai est de faire les devoirs et des révisions comme des feuilles de notes dans des cahier canada pour les matières les plus difficiles pour toi. Souvent je me met de la musique par dessus pour me calmer.
Re: Question
Bonsoir, DiamantDynamique4734!
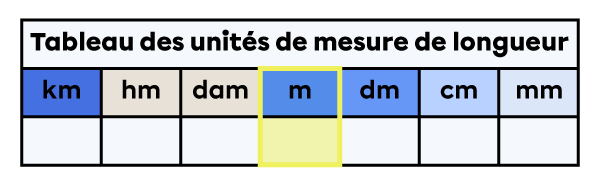
Au primaire, on fait la conversion des mesures de longueur.
Le premier tableau que tu as partagé est bon.
Pour convertir une mesure de longueur en une unité plus petite, je dois suivre les étapes suivantes.
- Je repère la colonne de l’unité de mesure de départ du nombre.
- Dans cette colonne, j’écris le chiffre à la position des unités.
- Je place les autres chiffres du nombre de façon à n’avoir qu’un seul chiffre par colonne.
- Je repère la colonne de la nouvelle unité de mesure.
- S’il y a une virgule, je la déplace à droite dans la colonne de la nouvelle unité de mesure.
- J’ajoute un 0 dans chaque colonne vide jusqu’à la colonne de la nouvelle unité de mesure.
Faisons un exemple, on convertit 459 m en cm.
1) Je repère la colonne de l’unité de mesure de départ du nombre.
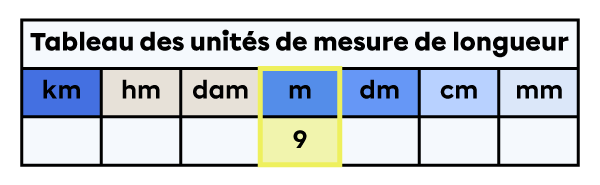
2) Dans le nombre 459, le chiffre à la position des unités est 9.
Dans cette colonne, j’écris le chiffre à la position des unités.
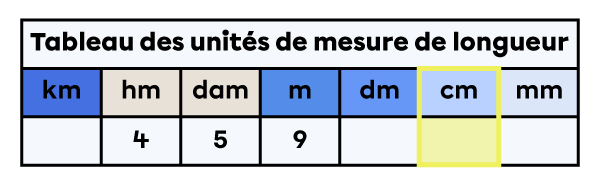
3) Je place les autres chiffres du nombre de façon à n’avoir qu’un seul chiffre par colonne.
4) Je repère la colonne de la nouvelle unité de mesure.
5) S’il y a une virgule, je la déplace à droite dans la colonne de la nouvelle unité de mesure.
Puisqu’il n’y a pas de virgule, je passe à l’étape suivante.
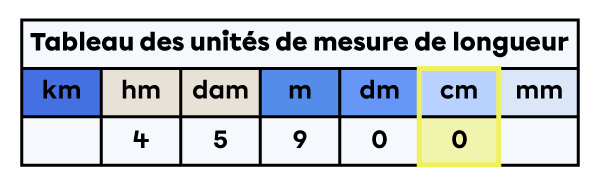
6) J’ajoute un 0 dans chaque colonne vide jusqu’à la colonne de la nouvelle unité de mesure.
459 m équivalent à 45 900 cm.
N'hésite pas à poser d'autres questions!
Re: Question
Bonjour OrnithorynqueOptimiste8838,
Il est normal d'avoir de la difficulté. Je vais donc te guider.
Voici un document qui devrait t'aider :
https://www.alloprof.qc.ca/fr/eleves/bv/francais/la-structure-d-un-texte-descriptif-f1439
Pour faire un bon texte descriptif, tu dois t'assurer de bien structurer ton texte en t'assurant de la présence de l'introduction, du développement et la conclusion. De plus, pour t'assurer de faire un bon texte, assure toi d'avoir des aspects et des sous-aspects tout en respectant un plan préparé qui mettra en valeur le sujet principal.
Je te conseillerais donc de faire une recherche à l'aide d'un plan que tu vas concevoir, puis de choisir les sujets et sous-aspects que tu veux aborder.
Au plaisir de t'aider, et n'hésite pas à revenir si tu as d'autres questions !
Bon travail,
OnyxIntergalactique1301
Re: Question
Bonjour SoleilInoubliable8340,
Merci beaucoup pour ta question! Bon poisson d’avril à toi également! 🐠
Tout d’abord, il existe des propriétés caractéristiques et des propriétés non caractéristiques. Les propriétés caractéristiques sont celles qui sont propres à une substance. La température d’ébullition ou la masse volumique en sont des exemples.
Ensuite, les propriétés non caractéristiques ne sont pas propres à une seule substance. On parle alors de la masse, du volume ou encore de la température. Voici une fiche qui pourrait t’aider :
J’espère avoir répondu à ta question. N’hésite pas à nous réécrire si des questions persistent!
Re: Question
Bonjour SoleilInoubliable8340,
Voici un document qui devrait t'aider :
https://www.alloprof.qc.ca/fr/eleves/bv/sciences/sciences-les-proprietes-de-la-matiere-s1002
Une propriété peut être physique (observée sans changer la nature de la substance) ou chimique (décrivant le comportement lors d'une réaction chimique). De plus, les propriétés peuvent être caractéristiques (uniques à une substance) ou non caractéristiques (communes à plusieurs substances). Dans le corps humain, de nombreuses substances se présentent sous forme de mélanges, souvent des solutions, dont l'étude des propriétés est intéressante.
Il y a également une vidéo pour te guider.
Au plaisir de t'aider, et n'hésite pas à revenir si tu as d'autres questions !
Bon travail,
OnyxIntergalactique1301
Re: Question
Bonjour,
Ton graphique représente la température moyenne à Paris.
De ce fait, si tu lis la température inscrite pour ton mois d'avril, tu obtiendras la température moyenne en avril.
Bonne journée :)
Re: Question
Bonsoir, JujubeCalme1293!
Merci d'utiliser la zone! Je peux certainement te donner quelques techniques de mémorisation.
Un élément clé pour apprendre par coeur est la répétition. Ceci te permettra d'approcher le jour de tes évaluations avec confiance.
Je te suggère donc d'étudier plusieurs fois les textes et les mouvements pendant des périodes d'environ 30 minutes et de prendre une pause après.
Faire de courtes périodes d'études pour donner un peu de repos à ton cerveau lui permettra d'emmagasiner l'information dans la mémoire à long terme.
Tu peux aussi te pratiquer seule et à voix haute. Imagine qu'un auditoire te fait face. Pratique aussi tes mouvements. Mémorise le plus possible l'ordre dans lequel tu devras présenter ton contenu.
N'attends pas à la dernière minute! Plus que tu es préparé, plus tu auras mémorisé tes textes et mouvements.
Si tu le souhaites, tu peux aller lire ces trucs pour la préparation d'un exposé oral :
Tu pourras utiliser mêmes techniques pour ton cours d'Art dramatique.
Je te souhaite une bonne préparation et n'hésite pas si tu as d'autres questions!
Iris :)