Best Of
Re: Question
Salut,
Merci d'utiliser la zone d'entraide.
C'est une bonne question. En fait, le programme d'éducation est construit un peu comme un château de Lego. Les nouveaux apprentissages sont compréhensibles parce que tu as des connaissances solides auparavant. Par exemple, il serait difficile d'apprendre les multiplications si tu ne comprends pas les additions.
Donc, il y a des moments dans l'année, où on s'assure que l'ensemble des élèves comprennent une notion pour aller un petit peu plus haut en suite.
Il n'y a pas des années où tu n'apprends pas de nouvelle chose, mais c'est vrai qu'il y a des moments où on s'assure que le sol est solide avant de continuer.
J'espère que ça t'aide à mieux comprendre cette situation.
Karen
Re: Question
Salut MentheRose9171 😁
Merci pour ta question!
Peux-tu nous envoyer en photo l'exercice avec lequel tu as de la difficulté? Ça nous permettra de mieux t'expliquer.
En attente de tes précisions. 😊
À tout de suite! 😎
Re: Question
Bonsoir, FraiseAdorable5247!
Voici les étapes à suivre afin de déterminer les zéros d'une fonction cosinus sous la forme f(x)=acos(b(x−h))+k:
1) On détermine la période de la fonction grâce à la formule P = 2π / |b|.
$$ P = \displaystyle \frac{2 \pi}{ \mid b \mid} $$
2) On résout l'équation f(x)=0.
- On isole l'expression cos(b(x−h)).
- On cherche le ou les angles qui ont la valeur du cosinus. Il faut regarder dans le cercle trigonométrique si la valeur est remarquable, sinon, on peut utiliser la calculatrice avec la fonction arc cosinus.
- Chacun des angles précédents est égal à l'expression b(x−h), on isole alors x.
3) On donne l'ensemble-solution en tenant compte de la période de la fonction.
Contrairement aux exemples de la fiche, tu travailles avec un intervalle précis, donc tu dois t'assurer que les valeurs trouvées s'y trouvent, sinon rajoute des tours.
N'hésite pas à poser d'autres questions!
Re: Question
Bonjour CitronSigma,
Merci de faire appel à nos services! :)
C'est une très bonne question!
Après enquête, nous avons une réponse pour toi: notre jeu le plus populaire est « Potager en péril ».
N'hésite pas à nous réécrire si tu as d'autres questions! :)
Marilee
Re: Question
Bonjour CrocodileArtistique9513,
Merci beaucoup pour ta question! Selon moi, oui, tu dois te servir des incertitudes des instruments de mesure afin de trouver celle du rendement énergétique. Toutefois, les incertitudes que tu devras utiliser sont celles de la masse et de la température. Voici une fiche qui pourrait t’aider :
J’espère avoir répondu à ta question. N’hésite pas à nous réécrire si des questions persistent!
Re: Question
Salut PotassiumTranquille6174 😁
Merci pour ta question!
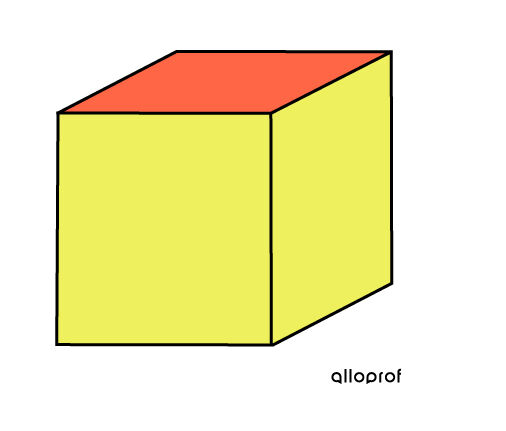
L'aire latérale, généralement notée AL, est la surface occupée par les figures qui ne servent pas de bases aux solides.
Par exemple, ici, ce sont les 4 faces en jaune qui représentent l'aire latérale (on imagine celles d'en arrière). Les deux faces en orange représenteraient les bases (on image celle d'en-dessous).
Pour en apprendre plus sur l'aire latérale, c'est par ici.
Écris-nous si tu as d'autres questions. 😊
À bientôt sur la Zone d'entraide! 😎
Re: Question
Salut,
Merci d'utiliser la zone d'entraide.
Pour t'aider à faire ton exercice, voici d'abord une définition des différentes sortes de rimes.
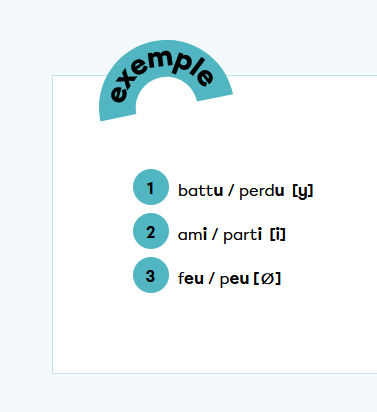
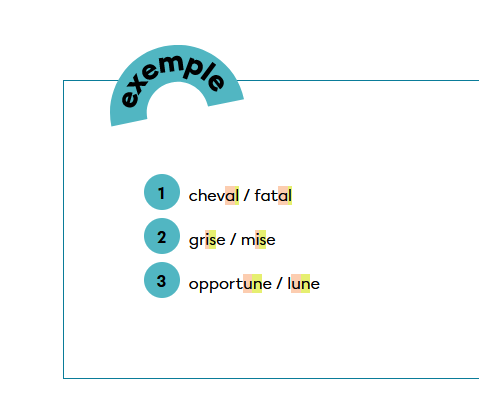
On dit qu'une rime est pauvre lorsqu’elle reprend un seul et même son.
Les rimes suffisantes ont deux sons en commun.
Si deux mots ont trois sons ou plus en commun, on dit que la rime est riche.
Pour les mots talent et équivalent, tu dois analyser la partie en gras et déterminer combien il y a de sons en suivant les exemples.
Indice : Il y en a plus qu'un. :)
Pour plus d'explications, c'est ici.
Bonne journée :)
Karen
Re: Question
Bonsoir, FraiseRose4867!
Par rapport à la première page, si jamais tu as besoin d'exemples pour les lois des exposants, consulte la fiche ci-dessous.
Par rapport à la première règle de l'exemple de la deuxième page, la valeur initiale est bien a=10 et le facteur multiplicatif est bien c=3. On dit que la situation arrive toutes les 15 minutes. Souviens-toi que, dans une heure, il y a quatre fois 15 minutes, d'où l'information que chaque heure renferme 4 périodes. Le nombre de fois que le facteur multiplicatif est appliqué dans une période donnée (x étant en heures) est donc b=4, pas 4x15. La fonction est
$$ f(x) = 10(3)^{4x} $$
Par rapport au numéro a) de la troisième page, tu as raison que a=50. Comme l'exercice précédent, le mot clé «triple» indique c=3. Selon l'énoncé, le temps x est en jours. C'est la période donnée. Si on triple à chaque heure, c'est qu'on triple 24 fois par jour, car il y a 24 heures dans une journée, donc b=24.
Nous avons bel et bien une fiche sur la résolution de problèmes impliquant la fonction exponentielle, vois le lien joint plus haut. Merci à toi de te fier à la zone et n'hésite pas à poser d'autres questions!