Best Of
Re: Question
Hi!
I'm not sure what your question is. Do you need some help with capitalization in English? If so, I suggest you read this factsheet :
Laurie :)
Re: Question
Salut BB8Turbo7021 😁
Merci pour ta question!
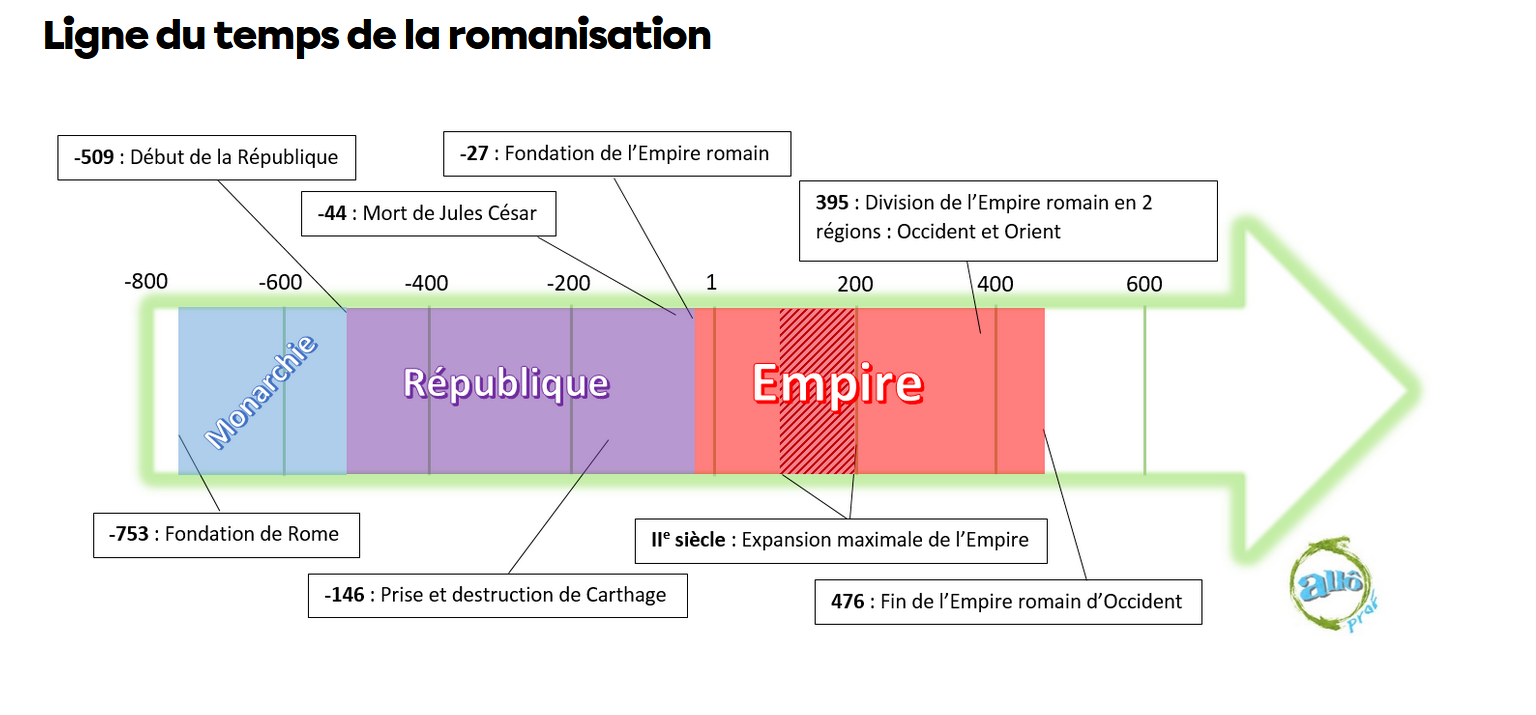
Cette ligne du temps pourra t'aider à compléter la tienne.
Pour plus de détails, c'est par là.
Écris-nous si tu as d'autres questions. 😊
À bientôt sur la Zone d'entraide! 😎
Re: Question
Salut!
Tu peux nous poser autant de questions que tu souhaites, ça nous fait plaisir de t'aider! :)
Le corrigé a raison. Nous avons vérifié si le coffre avait assez d'espace pour contenir les trois boites, mais nous avons oublié de vérifier aussi si une boite pouvait bien rentrer dans le prisme!
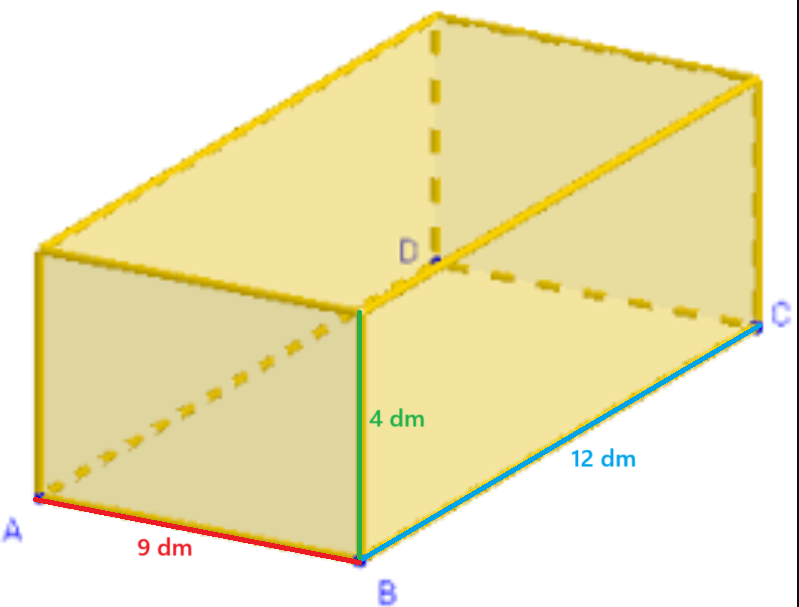
On a ce prisme (le coffre de la voiture) :
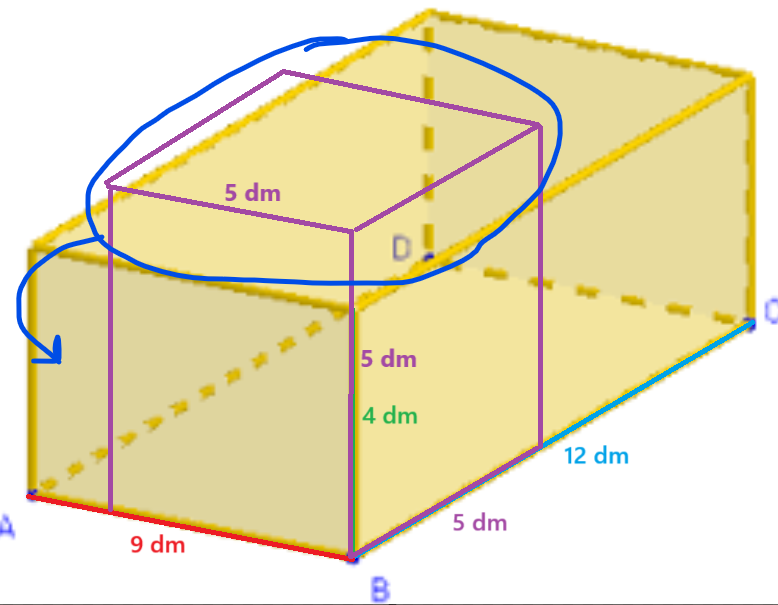
Le problème, c'est que le cube fait 5 dm de côté, et puisque l'une des mesures du prisme est inférieure à 5 dm, alors le cube ne pourra pas rentrer dans le prisme :
Le prisme a techniquement suffisamment d'espace pour contenir les trois cubes, puisque son volume est supérieur au volume des trois cubes, mais les dimensions posent problème! Il faudrait couper une partie des boites cubiques pour pouvoir les faire rentrer!
Par exemple, imaginons que les cubes sont des morceaux de gâteau et qu'on veuille les ranger dans un contenant qui est le prisme rectangulaire. Pour les faire rentrer, il faudrait couper une partie de chaque morceau, puis mettre ces morceaux coupés dans l'espace libre du contenant.
Dans cet exercice, puisque les cubes sont des boites et qu'on ne peut pas les couper, alors il sera impossible de faire rentrer les cubes dans le coffre.
Ainsi, nous aurions pu résoudre cet exercice sans faire aucun calcul, il suffisait de remarquer que les dimensions du cube (5 dm) sont supérieures à l'une des dimensions du prisme (4 dm) pour conclure que c'est impossible!
Voilà! Je pense que le but de cet exercice était justement de réfléchir à ce petit piège, il nous a bien eus toutes les deux 😆.
Si tu as d'autres questions, n'hésite pas, on est là pour ça! :)
Re: Question
Salut,
Merci d'utiliser la zone d'entraide.
C'est une bonne question, la différence entre les deux est la structure du verbe et le moment où se passe l'action.
Pour le conditionnel présent, il est utilisé lorsqu'une action pourrait se produire dans le présent ou dans le futur, à condition qu'une certaine situation arrive.
La structure est alors would + la base du verbe.
Par exemple: She would help you if she knew how.
Quant au conditionnel passé, il est utilisé pour parler d'une action qui aurait pu se produire dans le passé, mais qui n'a pas eu lieu puisqu'une condition n'était pas remplie.
La structure est alors would have + participe passé.
Par exemple: I would have gone to the pool if i had time.
J'espère que ça t'aide,
À bientôt,
Karen
Re: Question
Re salut!
Oh! Je n’avais pas vu ta question, désolé! Petit conseil, pour les prochaines fois, je te conseille de publier une nouvelle question au lieu de modifier une question déjà posée. De cette façon, on est sûr de ne pas la manquer :) (car malheureusement, on ne reçoit pas de notification lorsque des questions sont modifiées 😣).
Concernant ce problème, tu as un prisme rectangulaire dont les dimensions sont 12 dm × 9 dm × 4 dm. Si on multiplie ces mesures, on obtiendra le volume du prisme :
$$Volume_{prisme}=12 \times 9 \times 4 = 432 dm³$$
(N'oublie pas le petit ³ dans tes unités lorsque tu travailles avec des unités de volume ;) )
Les boites sont des cubes de 5 dm de côté. Pour calculer le volume d'un cube, on multiplie trois fois la mesure de côté par elle-même, ce qui revient à affecter un exposant 3 à la mesure du côté!
$$Volume_{cube}=5 \times 5 \times 5 = 5^3=125 dm³$$
Maintenant qu'on a le volume des deux solides (le prisme et le cube), on peut déterminer si on peut placer trois cubes dans le prisme. Pour cela, on doit vérifier si le volume total de trois cubes de 125 dm³ chaque est inférieur ou non au volume du prisme, qui est de 432 dm³.
Je te laisse continuer avec ces indices. Reviens nous voir si tu as besoin d'aide pour compléter l'exercice ou si tu souhaites que l'on vérifie ta réponse! :)
Re: Question
Salut!
Tu as raison, excuse-moi, c'est mon erreur! Il commence à être tard et je pense que mon cerveau devient fatigué! 😅😴 Je me suis trompée, j'ai mis 3 dm comme mesure de côté du cube au lieu de 5 dm. J'ai corrigé l'explication :)
Ainsi, tu as un volume total de 375 dm³ pour les trois cubes, et un volume de 432 dm³ pour le prisme. Puisque 375 dm³ < 432 dm³, alors il y a assez d'espace dans le coffre pour contenir les trois boites cubiques. Il restera même de la place, 57 dm³ pour être précis (432 dm³ - 375 dm³ = 57 dm³).
Désolé encore pour la confusion! J'espère que cela t'aide malgré tout. Reviens nous voir si tu as d'autres questions! :)
Re: Question
Bonsoir, DragonBionique7124!
Tu dois associer le graphique à la bonne règle.
Lorsque le graphique illustre une fonction constante (vois l'image plus bas), la règle a la forme y=b.
Par exemple, dans ton cas, on associe le graphique 2) à l'équation A).
Lorsque le graphique illustre une fonction linéaire, la règle a la forme y=ax.
Lorsque le graphique illustre une fonction de variation partielle, la règle a la forme y=ax+b.
Si la fonction est décroissante, a est négatif.
Lorsqu'une fonction est inverse, la règle a la forme y=k/x.
N'hésite pas à poser d'autres questions!
Re: Question
Salut!
Une liaison fixe est un type de liaison entre deux pièces d’un objet qui ne permet aucun mouvement entre elles. Elles sont complètement immobiles l'une par rapport à l'autre. À l'inverse, une liaison mobile permet un mouvement entre les pièces liées.
Ainsi, pour déterminer si une liaison est fixe ou mobile, tu peux te poser la question: "est-ce que la liaison permet à mon objet de bouger librement?".
Par exemple, une planche de bois collée ou vissée sur un plancher ne peut pas bouger, donc la liaison est fixe. À l'inverse, les deux branches d'une paire de ciseaux peuvent bouger entre elles: la liaison est mobile.
Dans le cas de ton nichoir à oiseaux, les parties qui sont solidement attachées ensemble pour rester en place sont des liaisons fixes! Par exemple, tu pourrais trouver sur ton nichoir un clou ou une vis. Quand tu fixes les parois du nichoir ensemble avec des clous ou des vis, elles ne peuvent plus bouger. Donc, c’est une liaison fixe! Tu pourrais aussi retrouver de la colle (forte), et puisque les pièces sont collées de façon permanente et ne bougent plus, alors cela est un autre type de liaison fixe.
Ainsi, regarde bien où les différentes pièces de ton nichoir sont attachées et demande-toi si elles peuvent encore bouger entre elles. Si la réponse est non, tu as trouvé une liaison fixe! ;)
Voici une fiche sur les liaisons qui pourrait t'être utile : La liaison | Secondaire | Alloprof
J'espère que cela t'aide! Si tu as d'autres questions, n'hésite pas à nous réécrire! :)
Re: Question
Salut!
Je suis contente que mon explication t'ait été utile :)
Comme ma collègue Mélissa t'a expliqué, la principale différence entre les taxes et les rabais, c'est l'opération mathématique qu'on utilise (addition ou soustraction)!
Dans les deux cas, on commence par calculer le % du prix, et ce, à l'aide de l'une des méthodes que tu avais inscrites sur ta feuille résumée. Si on parle des taxes, alors ce montant sera le montant des taxes à payer, et si on parle de rabais, alors ce sera le montant économisé.
Ensuite, on doit additionner ce montant de notre prix initial si ce sont des taxes, ou on doit soustraire ce montant de notre prix initial si c'était un rabais.
Tu obtiendras ainsi le montant après taxes ou après rabais :D
Par exemple, si on a un article à 20$, et que les taxes à payer sont de 15%, alors on commence par calculer le 15% de 20$ :
$$ 0,15 \times 20$ = 3$ $$
Ce qui nous donne 3$. En d'autres mots, 3$ est le montant que l'on paie pour les taxes, c'est ce 3$ que le gouvernement va percevoir. Si on veut connaître le montant après taxes, tu n'as qu'à additionner le 3$ au 20$, ce qui nous donne 23$.
Pour un rabais, c'est le même principe, sauf que l'on va soustraire le montant économisé du prix initial pour avoir le prix après rabais. Ainsi, si on reprend notre exemple, mais cette fois-ci, 15% est le pourcentage de rabais, alors la première étape reste la même :
$$ 0,15 \times 20$ = 3$ $$
3$ sera cependant ici le montant économisé. Donc, pour avoir le prix après rabais, il faut soustraire 3$ de notre 20$, ce qui nous donne 17$.
En résumé, les rabais, c’est quand on réduit le prix d’un article, tandis que les taxes, c’est un montant supplémentaire qu’on ajoute au prix d’un article.
Dans la vraie vie, il arrive souvent qu'on ait les deux en même temps sur une facture : un rabais et des taxes! Par exemple, je pourrais acheter un vélo à 150$ à 40% de rabais, mais puisque j'habite au Québec, il y aura 15% de taxes à payer. Dans ce cas, on peut commencer par calculer le montant économisé en calculant le 40% de 150$. On soustrait ensuite ce montant de notre prix initial de 150$, ce qui nous donne le prix après rabais. Puis, on doit calculer le 15% de taxes sur ce nouveau prix, et additionner le montant des taxes, ce qui nous donne au final le montant après rabais et après taxes :D Note que tu peux aussi faire l'inverse, c'est-à-dire commencer par les taxes, puis appliquer ensuite le rabais, c'est comme tu veux, la réponse finale sera la même! :) Par convention (et c'est ce que tu peux voir dans une vraie facture), on applique le rabais d'abord, et ensuite les taxes.
En ce qui concerne les exercices, ceux que Mélissa t'a proposés sont excellents, je te conseille de commencer par ceux-ci, puis, si tu en cherches d'autres par la suite, reviens nous voir!
Voilà! J'espère que c'est plus clair pour toi! :)
Re: Question
Bonjour,
Merci d'utiliser la zone d'entraide.
Malheureusement, pour identifier si un nombre est premier ou composer, il est nécessaire de le décomposer. Il n'existe pas d'autres méthodes.
Peut-être que cette vidéo pourra vous aider à mieux comprendre la méthode à utiliser:
N'hésitez pas à revenir nous voir si vous avez d'autres questions.
Karen