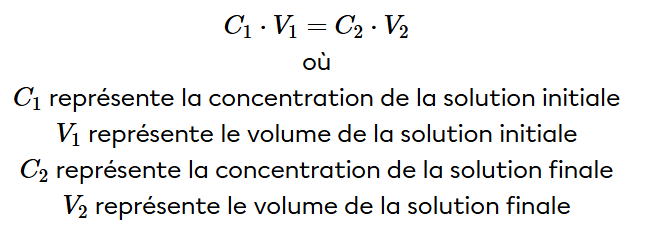Best Of
Re: Question
Bonjour LoutreEfficace6092,
Merci pour ta question !
Voici quelques trucs pour mieux étudier :
- Cible tes priorités : Consulte ton horaire d’examen afin de te concentrer en premier sur les matières dont l’examen approche le plus rapidement.
- Organise-toi à l’avance : Découpe ton étude en plusieurs parties. Cela peut sembler décourageant, mais je sais que tu es capable !
- Adopte une routine efficace : Étudie chaque soir par blocs de 30 minutes, en prenant des pauses régulières pour mieux assimiler l’information.
- Varie tes méthodes d’étude : Lis tes notes de cours, consulte nos fiches, regarde nos vidéos et joue à nos jeux interactifs !
- Choisis un environnement calme : Réduis les distractions pour rester concentré(e).
- Prends soin de toi : Une bonne alimentation, un sommeil réparateur et des habitudes de vie saines aident ton cerveau à mieux se concentrer !
- Pour des trucs supplémentaires, tu peux consulter notre fiche juste ici: https://www.alloprof.qc.ca/fr/eleves/bv/exams-et-trucs/trucs-pour-etudier-t2000
J’espère que ces conseils t’ont aidé ! Si tu as d’autres questions, n’hésite pas à revenir nous voir. 😊
Bonne journée ! 🌟
Re: Question
Un nombre décimal, c'est un nombre à virgule. Dans le fond, c'est un nombre non complet, donc qu'il en manque un peu pour que cela fasse un entier.
Désolé si l'expliquation est mauvaise, je ne suis pas prof. J'espère que tu comprend mieux les nombres décimaux!
Question
Bonjour! Chaque semaine jai des petit probleme de math et jaurais besoin de l'aide de quelqun. Voici le probleme:Tom travaille dans grand un edifice. Il se situe presentement au 4e etage . L'homme d'affaires monte jusqu'au 23e etage. Il redescend de 6 etages pour finalement remonter de 12 etages. A quel etage Tom est-il rendu? J'ai besoin d'explications plus clair. Merci!
Re: Question
Bonjour CentaureAdmirable3997!
Merci de faire appel à nos services!
Je comprends que tu doives répondre à la question que tu nous soumets.
Il faudrait par contre nous indiquer un peu le contexte derrière la question, par exemple s'il s'agit d'une question en lien avec un texte à lire, ou encore, nous fournir les informations qui t'ont été données avec l'exercice.
Ceci nous aiderait mieux à comprendre comment tu aimerais que nous t’aidions.
Si tu as besoin d'aide pour comprendre la question à cause de la manière dont elle est écrite, voici une autre formulation :
Esméralda a cherché le nain pendant un certain nombre d'heures. Avec les indices donnés, quelle est la plus longue durée durant laquelle elle aurait pu le chercher? Comment es-tu arrivé à cette réponse?
Nous attendons tes précisions et nous t’aiderons avec plaisir!
Iris :)
Re: Question
Bonjour,
Merci pour votre question!
Il s'agit des différentes étapes pour faire une enquête sur un sujet donné. Vous pouvez commencer par compléter l'étape 1, qui est de créer une question.
Votre enfant a-t-il ou a-t-elle reçu une consigne plus précise concernant les attentes du travail à effectuer?
N'hésitez pas à faire appel à nos services à nouveau. 😊
Re: Question
Bonjour AiguemarineChouette1176,
Merci pour ta question :)
Il s'agit ici d'un problème qui utilise le concept de dilution. La dilution est un procédé utilisé pour diminuer la concentration d’une solution en y ajoutant du solvant sans changer la quantité de soluté. Pour faire des calculs de dilution, tu devras utiliser la formule suivante:
La clé pour résoudre les problèmes de dilution, c'est d'identifier quelle information correspondent à quelle variable. Par exemple, on te dit que la solution à partir de laquelle tu devras faire les deux autres solutions est concentrée à 5%. Ça signifie que notre C1=5%.
Ensuite, on te dit qu'on veut faire deux solutions de 100 mL, une à une concentration de 0,1% et l'autre à 0,5%. Tu devras faire deux calculs, l'un avec C2=0,1% et l'autre avec C2=0,5%. Cependant, comme les deux solutions que tu veux obtenir sont de 100 mL, le volume final à utiliser dans ces calculs est V2=100 mL.
Il ne te reste plus qu'à utiliser la formule précédente pour effectuer tes deux calculs afin de savoir quel volume de la solution initiale tu devras utiliser pour préparer tes deux solutions. La chose importante à noter est qu'il faut utiliser les mêmes unités de concentration et de volume dans la formule. Ça signifie que si tu utilises une concentration en pourcentage, elle doit être en pourcentage pour C1 et C2.
Pour consulter des exemples, je t'invite à regarder la page suivante: https://www.alloprof.qc.ca/fr/eleves/bv/sciences/la-dilution-c1v1-c2v2-s1054
N'hésite pas si tu as d'autres questions :)
Sandrine
Re: Question
Salut,
Merci d'utiliser la zone d'entraide.
Pour arriver à faire ces exercices, tu dois tout d'abord savoir ce qu'est le périmètre. Le périmètre est le contour d'une forme plane.
Tu dois donc trouver la mesure du contour de chacune des formes présentées.
Le deuxième élément est d'identifier les formes géométriques que tu retrouves dans chacun des exercices. Pour t'aider, tu retrouves principalement des moitiés de cercle et des triangles.
Tu dois porter également une attention particulière à inclure tous les côtés de chacune des formes.
Par exemple, pour l'exercice A, si tu observes bien la forme, tu peux constater que la forme présentée est en fait 4 demi-cercles qui entourent un carré. Donc que tu dois calculer la circonférence de 2 cercles, dont le diamètre est de 4.
Pour t'aider à retrouver les formules, voici une fiche sur le sujet:
J'espère t'avoir aidé.
Bon travail!
Karen
Question
Bonjour.
Je me demandais quand sortait le nouveau monde dans Magimot.
Merci d'avance!!!
FraiseFantastique1207
Re: Question
Bonjour!
Un nouveau monde se préparer effectivement dans Magimot! Reste à l'affût afin d'y jouer lorsqu'il sera disponible! :D
Si tu as d'autres questions, n'hésite pas à nous réécrire. Nous te répondrons avec plaisir!
Laurie :)