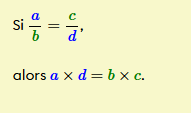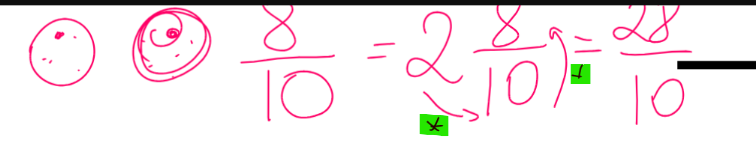Best Of
Re: Question
Bonjour XwingDiplomate6215,
Merci de faire appel à nos services!
Je ne suis pas sur à 100%, mais je pense sincèrement que le chiffre 1980 ou 1960 est un nom. En effet, ils représentent des années spécifiques, je penses donc qu'ils sont considérés comme des noms propres qui désignent une période spécifique dans le temps.
N'hésite pas à revenir nous voir si tu as d'autres questions.
PythonPerspicace8723
Re: Question
Salut DiamantJaune1219!
Merci d'avoir posé ta question sur la zone d'entraide :)
D'abord, les auxiliaires de conjugaison sont utilisés pour former les temps composés des verbes. Ils sont alors suivis d’un participe passé.
Je te suggère d'aller jeter un coup d'oeil à cette fiche : https://www.alloprof.qc.ca/fr/eleves/bv/francais/les-auxiliaires-f1073
N'hésite pas si tu as d'autres questions !
ZombieNoble190
Re: Question
Bonjour FraiseAdorable5247
Merci pour ta question!
Si tu dois exprimer les valeurs avec une incertitude relative, ta démarche semble correcte! Cependant, l'incertitude relative, qui est un rapport, est représentée en pourcentage. Tu peux donc laisser l'incertitude en pourcentage dans ta réponse.
De plus, je te conseille d'ajouter dans ton tableau les incertitudes que tu as calculées. Tu peux les placer dans la colonne des mesures de volume qui leur sont associées.
Finalement, je t'invite à revoir ton calcul pour la troisième constante, je crois qu'il y a une petite erreur de retranscription de données. :)
Voici une fiche explicative qui pourrait t'aider!
J'espère t'avoir aidé! N'hésite pas si tu as d'autres questions!
Re: Question
Bonsoir! :) Merci de nous écrire!
Si tu juges que faire une feuille de notes est la meilleure façon pour toi de retenir l'information, alors je t'invite à continuer à le faire, même si ça peut en effet être long. :)
Tu peux tout de même essayer de varier tes stratégies d'études; te faire des petites cartes d'étude, réciter à voix haute, utiliser des trucs mnémotechniques, faire une de nos Minirécups sont toutes des stratégies dont tu pourrais bénéficier.
Voici notre fiche Trucs pour mieux étudier qui te donne des trucs d'études en général.
Voici notre fiche Trucs pour étudier en histoire qui énumère plusieurs stratégies d'études pour l'histoire.
Bonne révision! :)
Sarah G
Re: Question
Bonjour OrTimide,
Merci pour ton initiative de venir vers nous!
Pour ton premier problème, il s'agit d'utiliser la méthode appelé le produit croisé ou le PEPM (Produit des extrêmes et produit des moyens). Cette technique consiste à multiplier les deux nombres qui sont obliques en fractions.
Une fois tes données multipliés, tu arrives avec une phrase algébrique que tu dois démêler afin de trouver la valeur du x. Pour cette exemple on arrive à :
2x * 6 = 5 * (x + 12)
12x = 5(x + 12)
À ce stade, je crois que tu peux prendre la relève et trouver la réponse.
Pour celui d'à côté, tu dois mettre tes fractions au même dénominateur vu que c'est une addition de fractions que tu dois faire. Ensuite, tu fais le produit croisé que je t'ai montré ci-dessus.
Pour le problème # 15, c'est une pure résolution algébrique que tu dois diviser en trois étapes :
1) Inconnus
2) Équation
3) Réponse
Les inconnus sont les mesures que tu ne connais pas mais qui te sont mentionnés dans le texte.
On te parle de la longueur et de la largeur d'un terrain.
Longueur : x (On ne le sait pas)
Largeur : x ÷ 2 + 1 (Un de plus que la moitié de la longueur*)
*Il faut connaître le vocabulaire en algèbre si tu n'es pas familier avec celui-ci.
Ensuite, l'équation qui te permettra de résoudre ta phrase et trouver le x. Dans le problème, on te dit que le périmètre est de 86 m. Instinctivement, tu sais qu'il te faut deux fois la longueur et deux fois la largeur pour trouver le périmètre, donc mis ensemble, cela fait :
2(x) + 2(x ÷ 2 + 1) = 86
J'ai foi en toi pour que tu trouves la valeur de x.
Une fois cette valeur trouvée, tu vas pouvoir procéder aux réponses.
Longueur : x =
Largeur : x ÷ 2 + 1 =
Et voilà. J'espère t'avoir donné un coup de main!
Surtout, ne lâche pas et persiste à poser des questions et à apprendre de tes erreurs. C'est l'effort qui compte!
QuartzSarcelle2575
P.S. Quelques fiches pour ta compréhension :
Re: Question
Il semble que ce soit un problème dans la précision des calculs.
Pour faire suite à l'explication que j'ai donnée précédemment
https://www.alloprof.qc.ca/zonedentraide/discussion/112951/question/p1
On a trouvé que y = a/(x-h) + 2
Avec les points (121,15) et (134,3) on obtient les équations
15 = a/(121-h) + 2 ou 13(121-h) = a (1)
3 = a/(134-h) + 2 ou 134 - h = a (2)
en égalant les a de (1) et (2) on trouve
13(121-h) = 134 - h
1573 - 13h = 134 - h
1439 = 12h et h = 1439/12 = 119.917
=> a = 134 - 119.917 = 14.083
et une fonction rationnelle: y = 14.083/(x - 119.917) + 2
avec x = 121 on obtient y = 15.004 (pour 15)
mais en utilisant h = 120 et a = 14 et y = 14/(x - 120) + 2 ce que j'ai fait initialement après avoir vu ton second message,
en prenant x = 121 on obtient y = 16 ! (pour 15)
Re: Question
Bonsoir, AraEnthousiaste1431!
La variable indépendante est la température en degrés Celsius.
La variable dépendante est la durée du cycle en minutes.
On a les deux points connus (121, 15) et (134, 3).
De plus, puisque la durée est supérieure à 2 minutes, on a l'asymptote horizontale k=2.
En posant ces données dans la règle d'une fonction rationnelle sous la forme canonique, on a un système de deux équations qu'on peut résoudre, car il reste deux variables inconnues, soit b et h.
$$ f(x)=\dfrac{a}{b(x-h)}+k $$
N'hésite pas à poser d'autres questions!
Re: Question
Salut!
Ici :
On représente les entiers par des cercles. Chaque cercle = 1 unité. Ainsi, 2 cercles et 8/10 représentent le nombre fractionnaire 2 \(\frac{8}{10}\). On peut ensuite transformer ce nombre fractionnaire en fraction. Pour cela, on multiplie l'entier par le dénominateur, et on additionne le numérateur.
Ce qui nous donne : 2 × 10 = 20, puis 20+8 =28, donc une fraction équivalente à 2 \(\frac{8}{10}\) est \(\frac{28}{10}\). On peut ensuite réduire cette fraction pour avoir une fraction irréductible.
Pour faire l'inverse, soit transformer une fraction impropre en un nombre fractionnaire, tu dois diviser le numérateur par le dénominateur. Le résultat sera un entier + un reste.
Tu dois ensuite garder cet entier, puis le faire suivre d'une fraction où le numérateur sera le reste trouvé et le dénominateur sera le même que celui de la fraction de départ. Voici un exemple :
$$ \frac{7}{2} = 7\div 2= 3 + reste ~de~ 1$$
On a divisé 7 par 2, ce qui nous donne 3 et un reste de 1 (7-6=1).
On garde l'entier 3, et on place le reste (1) dans une fraction dont le dénominateur est le même que celui de la fraction de départ 5/2, donc 2 :
$$ = 3 \frac{1}{2}$$
Je t'invite à consulter la fiche suivante : De la fraction au nombre fractionnaire et l'inverse | Secondaire | Alloprof
Et à revenir nous voir si tu as d'autres questions! :)
Re: Question
Bonjour à toi!
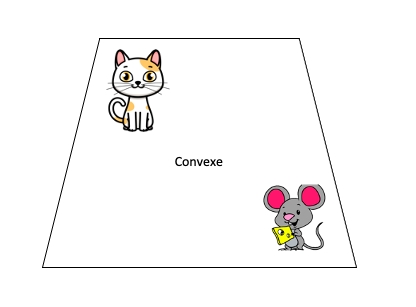
Voici des exemples qui pourraient t'éclairer! Un polygone convexe a des angles qui sont plus petits que 180°. Regarde bien les exemples ci-dessous.
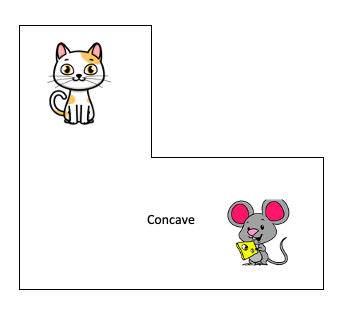
Un polygone non convexe (ou concave) a au moins un angle qui est plus grand que 180°. Donc, tu dois observer un angle rentrant dans ton polygone pour conclure que c'est un polygone non convexe. Regarde bien l'exemple ci-dessous.
Pour t'en souvenir, un truc souvent utilisé est celui du chat et de la souris! Par exemple, dans un polygone convexe, la souris n'a aucun endroit où se cacher du chat, alors que dans un polygone concave ou non convexe, la souris peut se dissimuler.
J'espère que cela t'a aidé à éclaircir tes questionnements. :D
N'hésite pas si tu as d'autres questions, ce sera un plaisir de te répondre!
Élizabeth