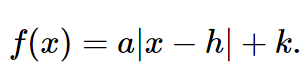Best Of

Salut!

L'algèbre est une branche des mathématiques qui utilise des lettres et des symboles pour représenter des nombres et exprimer des relations entre eux. Elle permet de résoudre des équations et de manipuler des expressions mathématiques de manière générale. Voici un exemple :

Imaginons que nous avons une boîte de bonbons. Nous ne savons pas combien il y a de bonbons dans cette boîte, alors nous dirons qu'il y a "x" bonbons. Si chaque bonbon coûte 2$, et qu'au total, nous payons 10$, alors nous avons l'équation :

$$ 2 \times x=10 $$

Cela signifie que le coût total des bonbons (2x) est égal à 10$. Maintenant, pour trouver combien de bonbons il y a dans la boîte, nous devons trouver la valeur de la lettre x. Pour ce faire, il faut résoudre cette équation algébrique. On trouvera alors que x=5, ce qui signifie qu'il y a 5 bonbons dans la boîte.

Si tu es curieux/curieuse d'en apprendre davantage à ce sujet, tu peux consulter la section "algèbre" de cette fiche : Aide-mémoire – Mathématiques – Secondaire 1 et 2 | Secondaire | Alloprof

As-tu une question spécifique par rapport à cette notion? Ou peut-être y a-t-il un exercice qui te pose problème? Si c'est le cas, je t'invite à nous réécrire pour nous faire parvenir ta question, ça nous fera plaisir de t'aider! :)

J'espère que cela t'aide! À bientôt! :)

Salut!

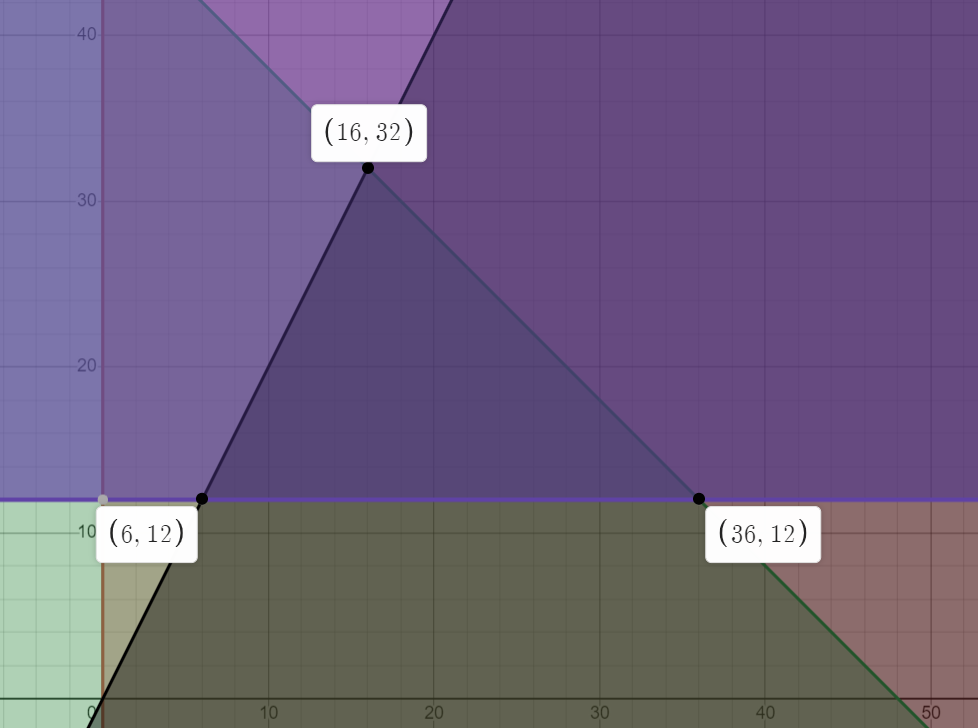
Tu avais initialement ce polygone de contraintes :

Ce contenu est protégé par le droit d'auteur. Toute reproduction à l'extérieur des forums Alloprof est interdite et pourra être considérée comme une violation du droit d'auteur.

Le maximum Z était bien 199, et le minimum 69.

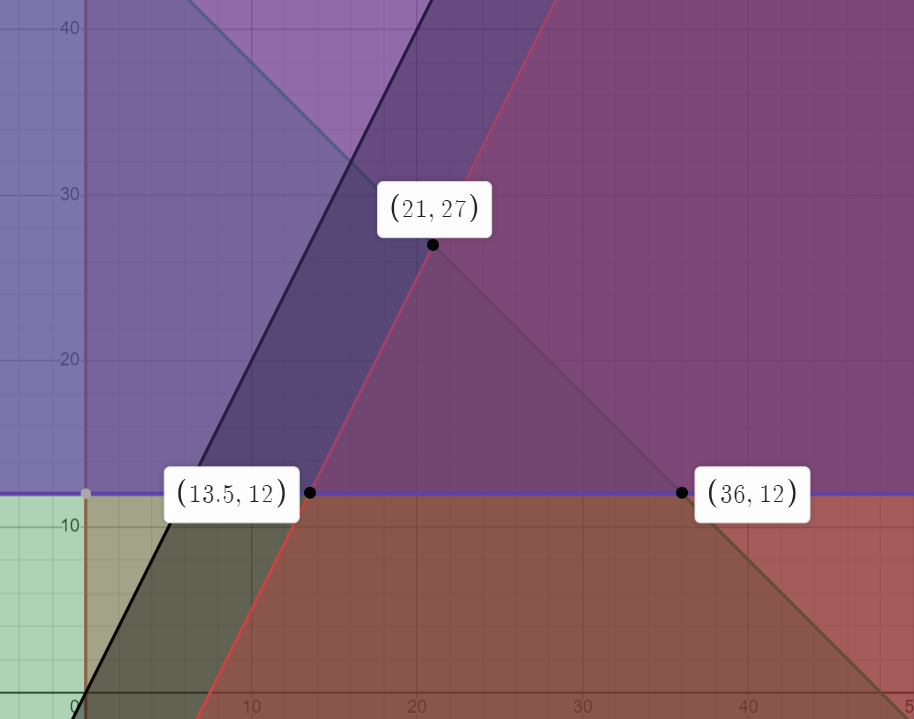
En ajoutant la contrainte, on a maintenant ce polygone de contraintes :

Ce contenu est protégé par le droit d'auteur. Toute reproduction à l'extérieur des forums Alloprof est interdite et pourra être considérée comme une violation du droit d'auteur.

Nous n'avons donc plus les mêmes sommets du polygone de contraintes, ce qui fait en sorte que le maximum Z devient 189 et le minimum devient 91.5.

Si tu calcules la différence entre les maximums et les minimums avant et après l'ajout de la contrainte, tu constateras que le minimum a augmenté de 22,5 :

$$91,5-69=22,5$$

et que le maximum a diminué de 10 :

$$199-189=10$$

Le maximum et le minimum changent, simplement parce que le polygone de contraintes change aussi. Les points initiaux (16, 32) et (6, 12) ne sont plus dans la région-solution avec l'ajout de la nouvelle contrainte.

Tu peux utiliser le logiciel Desmos pour t'aider à visualiser le polygone de contraintes : Desmos | Calculatrice graphique

J'espère que c'est plus clair pour toi! :)

Salut !

En général, pour déterminer le domaine, on se fie au restriction de la fonction. Pour la fonction rationnelle, la valeur du dénominateur ne peut pas être nulle.

\(\frac{a}{0}\) ne fait pas parti du réel. Dans ton cas, il n'y a pas de déphasage en \(x\), donc le domaine est bel et bien \(x \in \mathbb{R}^*\) et n'est pas qu'en positif.

J'espère que cela ait pu t'aider et si tu as d'autres questions, n'hésite pas !

Bonne soirée !

Salut!

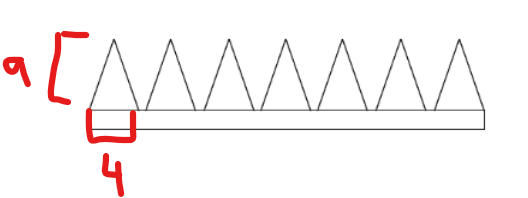
Tu as une fonction périodique composée de plusieurs petites fonctions valeurs absolues.

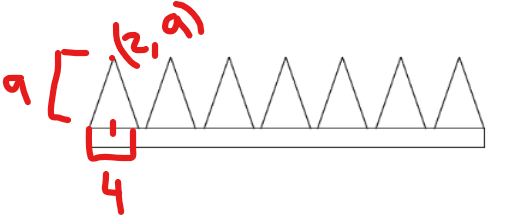
On te dit que les dents meurent 9 mm de hauteur et 4 mm de largeur :

Ce contenu est protégé par le droit d'auteur. Toute reproduction à l'extérieur des forums Alloprof est interdite et pourra être considérée comme une violation du droit d'auteur.

Ainsi, ces données te permettront de déterminer le sommet de chaque fonction valeur absolue, donc la valeur des paramètres h et k dans la règle :

Ce contenu est protégé par le droit d'auteur. Toute reproduction à l'extérieur des forums Alloprof est interdite et pourra être considérée comme une violation du droit d'auteur.

Ce contenu est protégé par le droit d'auteur. Toute reproduction à l'extérieur des forums Alloprof est interdite et pourra être considérée comme une violation du droit d'auteur.

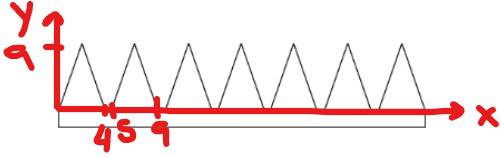
On nous dit aussi que chaque dent est espacée de 1 mm :

Ce contenu est protégé par le droit d'auteur. Toute reproduction à l'extérieur des forums Alloprof est interdite et pourra être considérée comme une violation du droit d'auteur.

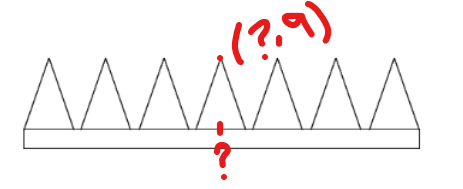
On cherche la règle de la 4e dent, soit la suivante :

Ce contenu est protégé par le droit d'auteur. Toute reproduction à l'extérieur des forums Alloprof est interdite et pourra être considérée comme une violation du droit d'auteur.

Tu peux trouver la valeur du paramètre h, la coordonnée en x du sommet, en utilisant le fait que la largeur des dents est de 4 mm et qu'elles sont espacées de 1 mm.

Puis, tu peux trouver les coordonnées d'un autre point de cette fonction (par exemple, les coordonnées d'une des abscisses à l'origine). Tu dois ensuite suivre cette démarche pour trouver la valeur du paramètre \(a\) :

Ce contenu est protégé par le droit d'auteur. Toute reproduction à l'extérieur des forums Alloprof est interdite et pourra être considérée comme une violation du droit d'auteur.

Voici une fiche sur cette notion qui pourrait t'être utile : Trouver la règle d’une fonction valeur absolue | Secondaire | Alloprof

J'espère que c'est plus clair pour toi! :Si tu as d'autres questions, n'hésite pas à nous réécrire! :)