Matières
Niveaux
Lorsqu’on cherche la règle d’une fonction valeur absolue, 3 cas sont possibles. Dans tous les cas, on utilise la forme canonique simplifiée : |f(x)=a\vert x-h\vert+k.|
Pour trouver la règle d’une fonction valeur absolue lorsqu’on connait les coordonnées du sommet et d’un point quelconque de la fonction, il suffit d’utiliser l’équation sous la forme canonique.
Remplacer les paramètres |h| et |k| par les coordonnées du sommet dans la règle.
Calculer |a| en remplaçant |x| et |y| par les coordonnées d’un autre point.
Écrire la règle.
Détermine la règle de la fonction valeur absolue dont les coordonnées du sommet sont |(-3, -2)| et les coordonnées d'un point sont |(-4, -5).|
Remplacer les paramètres |\boldsymbol{h}| et |\boldsymbol{k}| par les coordonnées du sommet dans la règle||\begin{align}f(x)&=a\vert x-\color{#3b87cd}h \vert +\color{#3a9a38}k\\f(x) &=a\vert x-\color{#3b87cd}{-3} \vert +\color{#3a9a38}{-2} \\ f(x) &= a\vert x+3\vert -2 \end{align}||
Calculer |\boldsymbol{a}| en remplaçant |\boldsymbol{x}| et |\boldsymbol{y}| par les coordonnées d’un autre point
||\begin{align} \color{#ff55c3}{-5} &= a\vert \color{#ff55c3}{-4}+3\vert -2 \\ -5 &= a\vert -1\vert -2 \\ -5 &= a(1)-2\\ -5 &= a-2\\ -3&=a \end{align}||
Écrire la règle
La règle de cette fonction est |f(x)=-3\vert x+3\vert -2.|

Moments dans la vidéo :
Pour trouver la règle d’une fonction valeur absolue lorsqu’on connait 2 points ayant la même ordonnée |(y)| et un autre point de la fonction, on doit trouver la pente des 2 branches de la fonction.
Placer les points dans un plan cartésien.
Calculer la valeur du paramètre |h| en faisant la moyenne des abscisses |(x)| des 2 points qui ont la même ordonnée |(y).|
Calculer la pente de la droite passant par les 2 points qui sont situés du même côté du sommet (sur la même branche).
Déterminer le signe du paramètre |a| en analysant l’ouverture de la fonction.
Remplacer dans la règle les paramètres |h| et |a| calculés précédemment.
Calculer |k| en remplaçant |x| et |y| par les coordonnées d’un point.
Écrire la règle.
Dans une fonction valeur absolue, les 2 branches sont symétriques. Ainsi, le paramètre |a| de la fonction valeur absolue, la pente de la branche de gauche |(a_1)| et la pente de la branche de droite |(a_2)| possèdent tous la même valeur si on ne tient pas compte de leur signe.
L’ouverture est vers le haut.
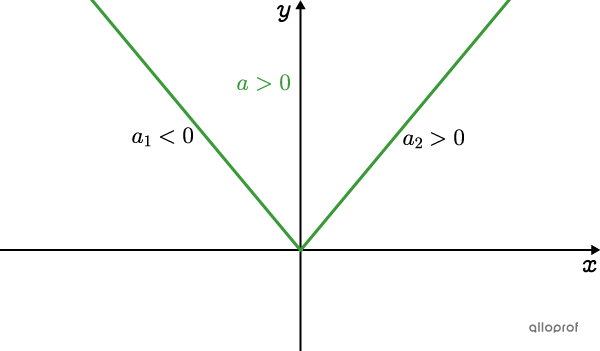
La pente de la branche de gauche est négative, car elle est décroissante |(a_1<0).|
La pente de la branche de droite est positive, car elle est croissante |(a_2>0).|
Le paramètre |a| de la fonction valeur absolue est positif |(\color{#3A9A38}{a>0}).|
L’ouverture est vers le bas.
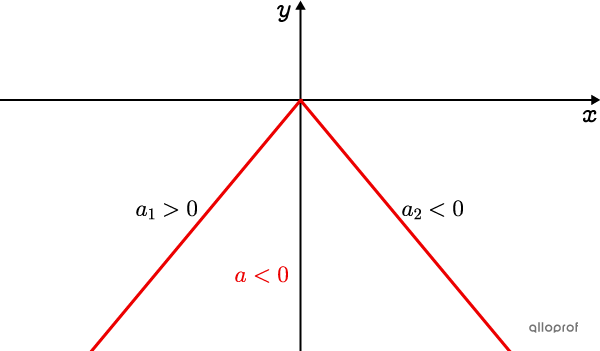
La pente de la branche de gauche est positive, car elle est croissante |(a_1>0).|
La pente de la branche de droite est négative, car elle est décroissante |(a_2<0).|
Le paramètre |a| de la fonction valeur absolue est négatif |(\color{#EC0000}{a<0}),| car la courbe a subi une réflexion par rapport à l’axe des |x.|
Détermine la règle de la fonction valeur absolue dont les zéros sont |-7| et |1| et qui passe par le point |(-9,-4).|
Placer les points dans un plan cartésien
En analysant leur position, on en déduit que les points |(-9,-4)| et |(-7,0)| sont situés sur la même branche de la fonction valeur absolue et que le point |(1,0)| est sur l’autre branche. Aussi, on en déduit que le sommet de la fonction sera au-dessus de l’axe des |x| et que l’ouverture sera vers le bas.
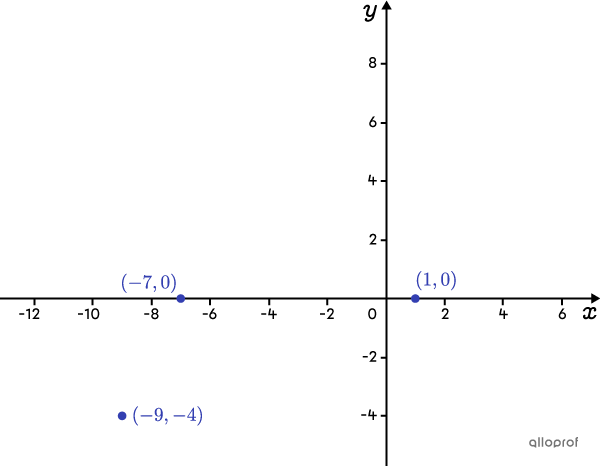
Calculer la valeur du paramètre |\boldsymbol{h}| en faisant la moyenne des abscisses des 2 points qui ont la même ordonnée
Dans l’exemple, les points ayant la même ordonnée sont les zéros, situés à |x=-7| et |x=1.| Le |x| du sommet, qui correspond au paramètre |h,| se trouve exactement au milieu des zéros étant donné que le graphique d’une fonction valeur absolue est symétrique. ||\begin{align}h&=\dfrac{-7+1}{2}\\h&=-3\end{align}||
Calculer la pente de la droite passant par les 2 points qui sont situés du même côté du sommet
Les points |(-9,-4)| et |(-7,0)| sont situés sur la même branche, à gauche du sommet. On calcule la pente de la droite |(a_1)| passant par ces points. ||\begin{align}a_1&=\dfrac{y_2-y_1}{x_2-x_1} \\ &=\dfrac{0--4}{-7--9} \\ &=2\end{align}||
Déterminer le signe du paramètre |\boldsymbol{a}| en analysant l’ouverture de la fonction
Sachant que l’ouverture est vers le bas, on en conclut que |a| est négatif. ||a=-2||
Remplacer dans la règle les paramètres |\boldsymbol{h}| et |\boldsymbol{a}| calculés précédemment||\begin{align}f(x)&=\color{#ec0000}a\vert x-\color{#3b87cd}h \vert +k\\f(x) &=\color{#ec0000}{-2}\vert x-\color{#3b87cd}{-3} \vert +k\\ f(x) &=-2\vert x+3 \vert +k\end{align}||
Calculer |\boldsymbol{k}| en remplaçant |\boldsymbol{x}| et |\boldsymbol{y}| par les coordonnées d’un point
On prends le point |(1,0).| ||\begin{align} \color{#ff55c3}{0} &= -2\vert \color{#ff55c3}{1}+3\vert +k \\ 0 &= -2\vert 4\vert +k \\ 0 &= -2(4) +k \\ 0&=-8+k \\ 8 &= k \end{align}||
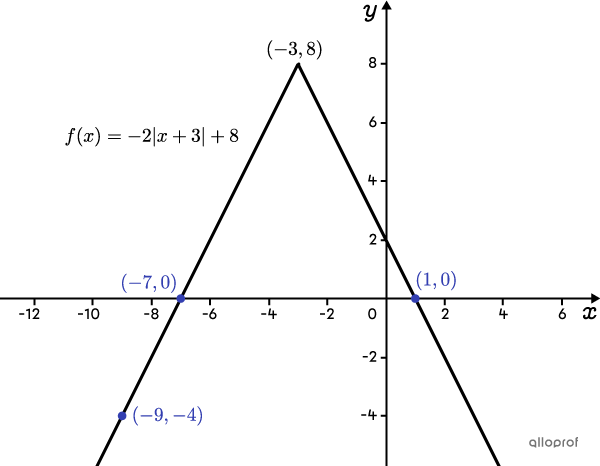
Écrire la règle
La règle de cette fonction est |f(x)=-2\vert x+3\vert +8.|

Moments dans la vidéo :
Pour déterminer quels points sont situés sur la même branche lorsqu’on a 3 points quelconques dans le graphique, il y a quelques éléments à respecter.
Il ne faut jamais tenir pour acquis que l’un des 3 points est le sommet de la fonction, à moins que ce soit précisé.
Il faut toujours s’assurer que la symétrie entre les 2 branches est respectée.
Soit la figure suivante.
Est-ce que ce sont les points |A| et |B| qui sont sur la même branche ou est-ce que ce sont les points |B| et |C|?
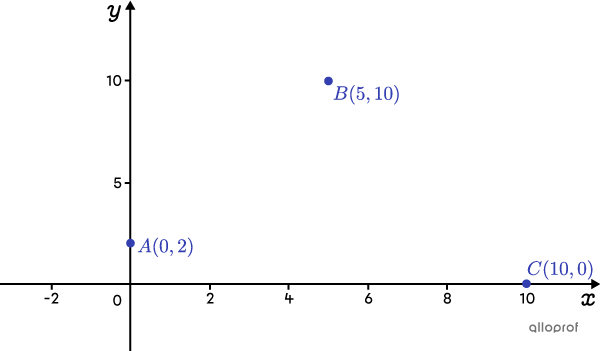
Si |A| et |B| sont sur la même branche, on peut alors calculer la pente de cette branche. ||a_1=\dfrac{10-2}{5-0}=\dfrac{8}{5}||
Comme les 2 branches doivent être symétriques, la pente de la droite symétrique passant par le point |C| est la même, mais négative. ||a_2=-\dfrac{8}{5}||
En traçant la droite |AB| et la droite passant par |C| dont la pente vaut |-\dfrac{8}{5},| on obtient ce graphique.
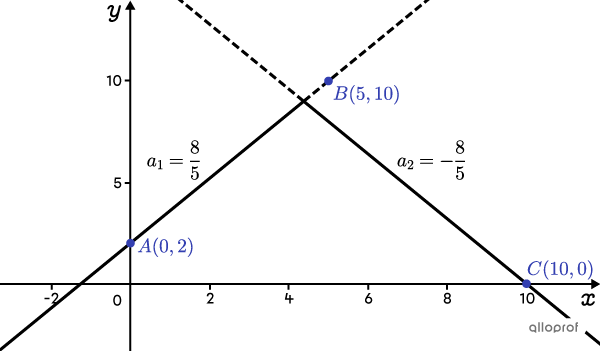
Avec ce choix, on remarque que le sommet est plus bas que le point |B.| Autrement dit, le point |B| n’est situé sur aucune des 2 branches de la valeur absolue, mais plutôt sur le prolongement d’une branche, ce qui veut dire qu’on a fait le mauvais choix.
Si on suppose plutôt que |B| et |C| sont sur la même branche, alors la pente de cette branche est |a_2=\dfrac{10-0}{5-10}=-2.| La pente de la branche de gauche est donc égale à |2| et on obtient le graphique suivant qui confirme que c’est le bon choix.

Dans tous les cas, on remarque que le point |B| n’est pas le sommet de la fonction.
Pour trouver la règle d’une fonction valeur absolue lorsqu’on ne connait ni les coordonnées du sommet ni celles de 2 points situés à la même hauteur (ordonnée) dans le plan cartésien, il faut faire un système d’équations et utiliser la méthode de comparaison. Voici la démarche à suivre.
Placer les points dans un plan cartésien.
Calculer la pente de la droite passant par les 2 points qui sont situés du même côté du sommet (sur la même branche).
Trouver la règle sous la forme |y=ax+b| des 2 branches.
Trouver les coordonnées du sommet situé à l’intersection des 2 branches à l’aide de la méthode de comparaison.
Déterminer le signe du paramètre |a| en analysant l’ouverture de la fonction.
Écrire la règle en remplaçant les paramètres |a,| |h| et |k| par leur valeur.
Détermine la règle de la fonction valeur absolue passant par les points |(1,2),| |(7,-6)| et |(-1,-2).|
Placer les points dans un plan cartésien
En analysant leur position, on remarque que les points |(-1,-2)| et |(1,2)| sont situés sur la même branche de la valeur absolue et que le point |(7,-6)| est sur l’autre branche. Aussi, on en déduit que le sommet de la fonction sera au-dessus de l’axe des |x| et que l’ouverture sera vers le bas.
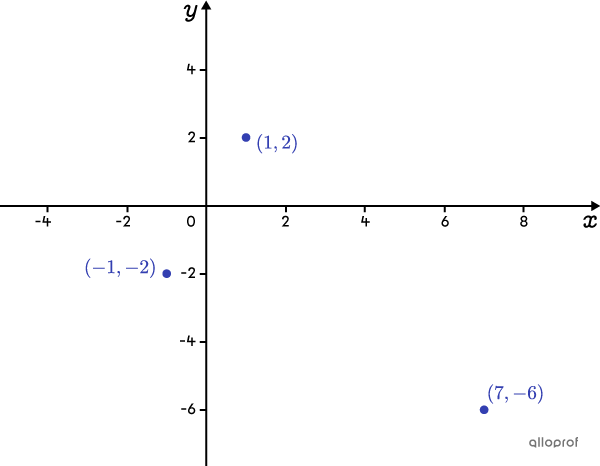
Calculer la pente de la droite passant par les 2 points qui sont situés du même côté du sommet
Les 2 points sur la même branche sont |(-1, -2)| et |(1,2).| ||\begin{align}a_1&=\dfrac{y_2-y_1}{x_2-x_1}\\&=\dfrac{2--2}{1--1}\\&=2\end{align}||
Trouver la règle sous la forme |\boldsymbol{y=ax+b}| des 2 branches
Pour la branche de gauche, on prend le |a| positif puisque la droite est croissante et on utilise le point |(-1,-2)| pour calculer |b_1.| ||\begin{align} y_1&=a_1x+b_1 \\ -2 &= 2 (-1) + b_1\\ -2 &= -2 + b_1 \\ 0 &=b_1 \end{align}||Donc, pour cette branche, la règle est |y_1=2x.|
Pour la branche de droite, on prend le même |a,| mais négatif. De plus, on utilise le point |(7,-6)| pour calculer |b_2.| ||\begin{align} y_2&=a_2x+b_2 \\ -6 &= -2 (7) + b_2 \\ -6 &= -14 + b_2 \\ 8&=b_2 \end{align}||Donc, pour cette branche, l'équation est |y_2=-2x+8.|
Trouver les coordonnées du sommet situé à l’intersection des 2 branches à l’aide de la méthode de comparaison ||\begin{align} y_1&=y_2 \\ 2x &= -2x + 8 \\ 4x&=8\\x&=2 \end{align}||Donc, |h=2.|
Pour |k,| on remplace |x| par |2| dans l'une ou l'autre des 2 règles. ||\begin{align} \begin{aligned}y_1 &= 2x \\ &= 2 (2) \\ &=4\end{aligned}\quad\ \ \begin{aligned}y_2 &= -2x+8 \\ &= -2 (2)+8 \\ &=4\end{aligned} \end{align}||Donc, |k=4.|
Déterminer le signe du paramètre |\boldsymbol{a}| en analysant l’ouverture de la fonction valeur absolue
Sachant que l’ouverture est vers le bas, on en conclut que |a| est négatif.
Donc, |a=-2.|
Écrire la règle en remplaçant les paramètres |\boldsymbol{a},| |\boldsymbol{h}| et |\boldsymbol{k}| par leur valeur
En utilisant la règle sous la forme canonique, on obtient ceci. ||\begin{align}f(x)&=a\vert x-h\vert +k\\\\f(x)&=-2\vert x-2\vert +4\end{align}||
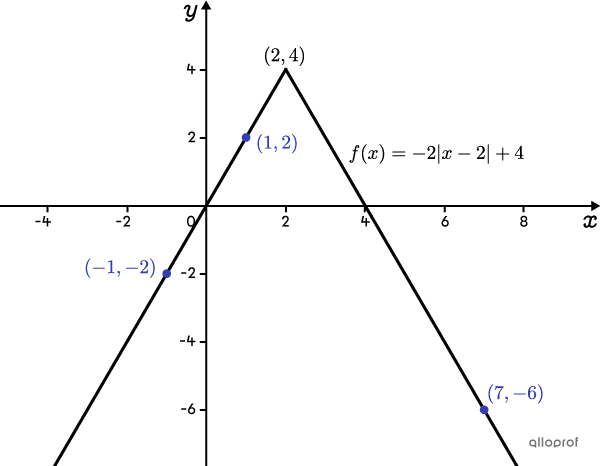

Moments dans la vidéo :