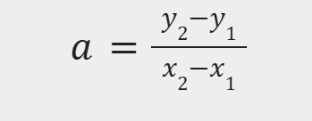Best Of
Re: Question
Bonjour! :) Super suggestion! Merci!
Tu peux la partager ici: https://alloprof-ti.atlassian.net/servicedesk/customer/portal/6/group/37
En attendant, nous en avons quelques-uns déjà sur Grimoire https://www.alloprof.qc.ca/fr/eleves/bv/jeux/grimoire
Merci beaucoup pour ta contribution! C'est grâce à des gens comme toi qu'Alloprof continue de s'améliorer de jour en jour! :)
Sarah G
Re: Question
Bonjour,
J'ai déjà abordé ce sujet dans une précédente explication, jettes-y un œil :
Si tu as d'autres questions, n'hésite pas à venir les poser !
Bonne journée :)
Re: Question
Bonsoir DiamantRose9777, merci pour ta question !
Il est quand même possible de résoudre ton exercice malgré l'absence de OH du côté des réactifs. N'oublie pas que OH signifie que tu as un atome d'oxygène et un atome d'hydrogène, même mis entre parenthèse, ça ne change pas le fait que ce sont deux atomes distinct. Cela veut dire que si tu as (OH)2, cela veut dire que tu as deux groupes -OH, cela revient donc à avoir 2 atomes d'oxygènes et 2 atomes d'hydrogènes. Tu peux donc équilibrer ces deux types d'atomes avec la molécule d'eau H2O !
J'espère que ça a pu te débloquer, si tu as besoin de plus de précision ou si tu veux qu'on t'aide dans ta démarche, n'hésite pas à nous réécrire !
Re: Question
Salut !
L'astronaute est en effet un système à elle-même, mais dans ton cas, il est question de l'ensemble de l'astronautes dégustant un chocolat chaud. Cela implique le système intérieur de la station pour inclure l'action de boire du chocolat chaud. Ainsi, si le système représente l'intérieur de la station, alors l'environnement est l'espace à l'extérieur.
Si on pense tout simplement à l'astronaute, alors il s'agit d'un système ouvert où il y a des échanges de matières (chocolat chaud) et d'énergie (chaleur de la boisson).
J'espère que cela ait pu t'aider et si tu as d'auitres questions, n'hésite pas !
Bonne journée !
Re: Question
Salut !
Selon le site de Institut de tourisme et d’hôtellerie du Québec, c'est : Diploma of Collegial Studies (DCS) in Techniques de tourisme
*DCS c'est l'abréviation de diploma of Collegial Studies
Re: Question
Bonjour,
Pose-toi toujours la question suivante : quelle variable dépend de l'autre ? Ou bien : quelle variable est influencée par l'autre ?
ex: L’effet de la caféine sur le sommeil.
Ici, c'est le sommeil qui dépend de la quantité de caféine et non l'inverse. En d'autres mots, la quantité de caféine influence le sommeil.
De ce fait, la variable dépendante (y) c'est le sommeil et la variable indépendante (x) c'est la quantité de caféine.
Voici un lien utile:
Bonne journée :)
Question
Bonjour, je me demandais comment traduit-on un 'DEC en technique en tourisme' en anglais pour l'écrire dans un CV?
Merci d'avance!
Re: Question
Salut!
Un adjectif qualifiant est un adjectif qui va donner une qualité (positive, négative ou neutre) au nom ou au pronom qu'il accompagne. Voici quelques exemples:
- La pomme est succulente. (Qualité positive)
- Le dessert est sucré. (Qualité neutre)
- Le décor est laid. (Qualité négative)
L’adjectif classifiant, quant à lui, va permettre de catégoriser et de classifier les noms ou les pronoms qu'il accompagne. Exemples:
- Il a rejoint l'équipe canadienne de soccer. (L'adjectif canadienne nous permet de savoir quelle équipe il a rejointe)
- Ma mère aime la cuisine orientale. (L'adjectif orientale nous permet de savoir quel type de cuisine ma mère aime).
Petit truc pour distinguer l'un de l'autre: On peut souvent mettre l'adverbe très devant un adjectif qualifiant, alors qu'il ne fait aucun sens de le mettre devant un adjectif classifiant.
Si tu veux en savoir plus sur les exceptions et sur comment reconnaître ses deux types d'adjectifs, je te suggère de consulter cette fiche Alloprof : L’adjectif qualifiant et l’adjectif classifiant | Alloprof
Si tu as d'autres questions, n'hésite pas à nous réécrire! 😁☃️
Re: Question
Salut!
C'est super gentil de ta part de prendre le temps de nous communiquer ton amour pour Magimot et Grimoire! Notre équipe apprécie toujours recevoir des commentaires sur ses jeux :D
N'hésite surtout pas à nous réécrire si tu as d'autres questions! À bientôt! 😁☃️
Re: Question
Salut !
Pour ce numéro, il faudra utiliser cette formule (C'est une des méthodes qu'il y a) :
Pour commencer le calcul, utilisons ses informations :
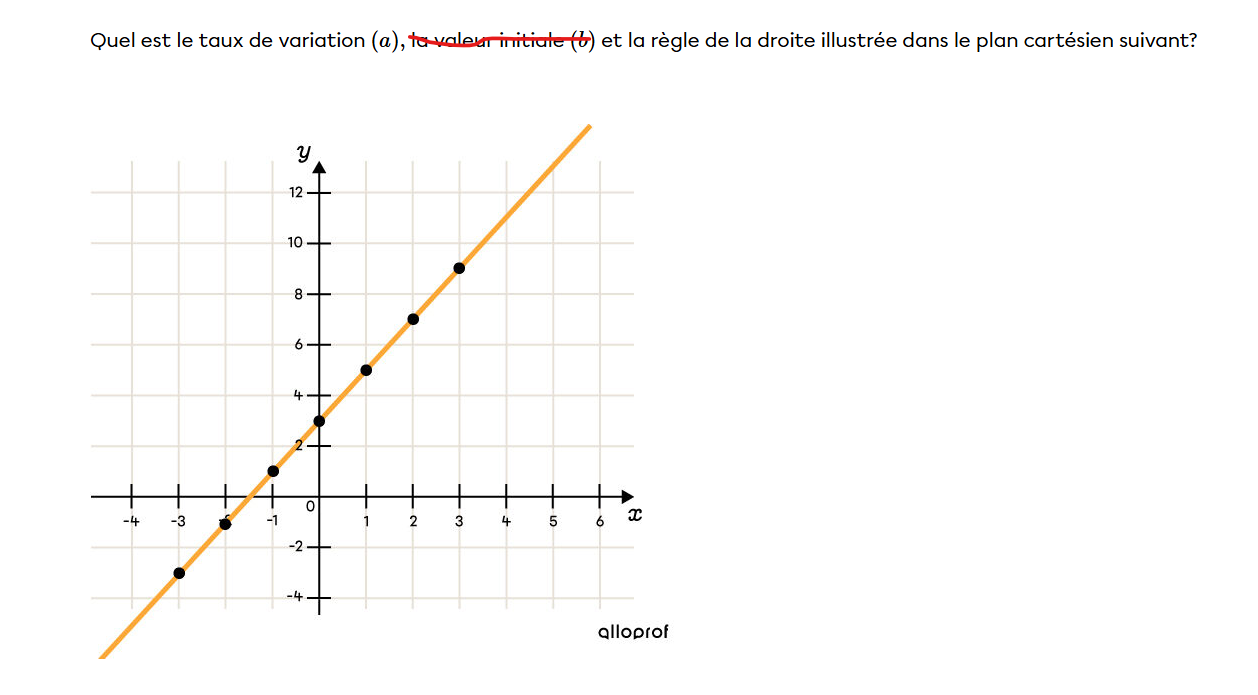
qui donne les points (0,40) et (3,3 ; 15)
*(0,40) est l'ordonnée à l'origine comme tu as pu le constater dans ton graphique
Ensuite, tu prends ces points est tu les met dans la formule pour les calculer, ce qui donnera le taux de variation
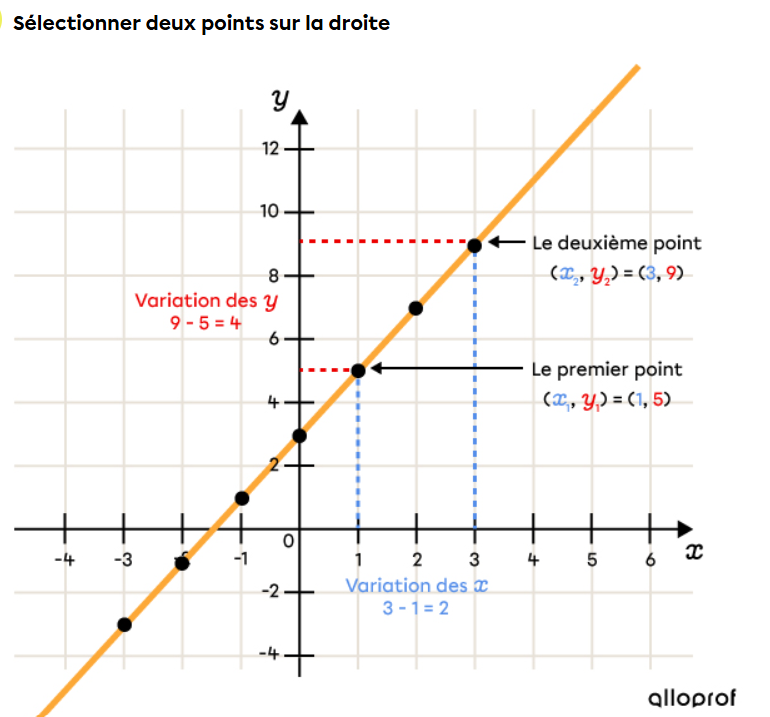
Voici un exemple d'Alloprof :
Voilà ! J'espère t'avoir aidé :)