Best Of

Salut!

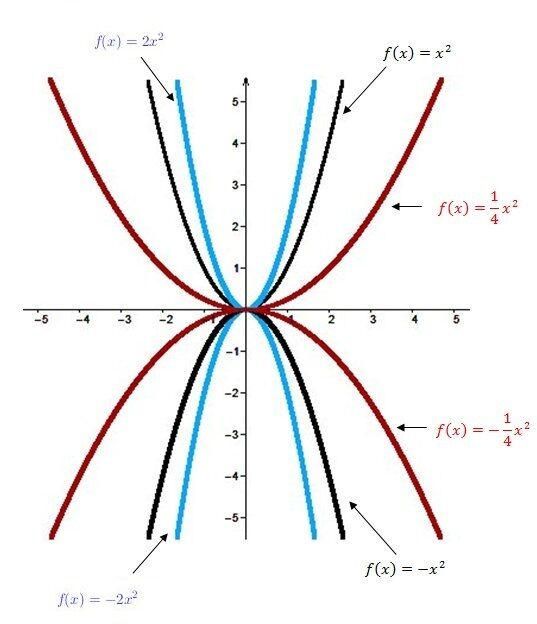
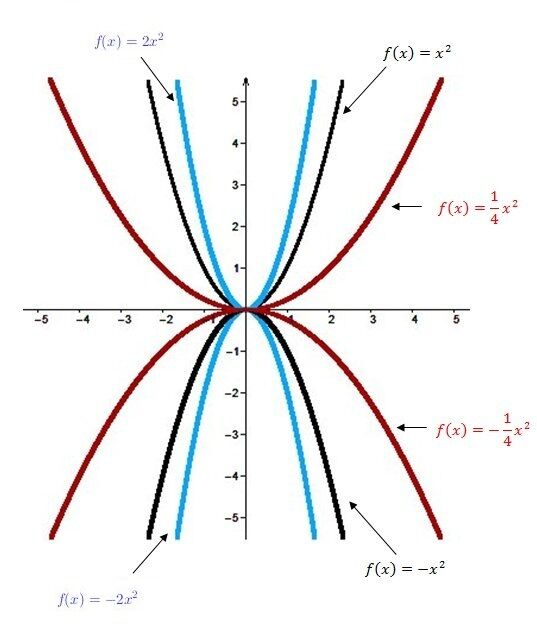
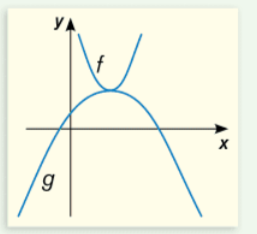
Analysons l'effet du paramètre a sur la parabole d'une fonction de second degré.

Le signe du paramètre a nous donne l'orientation de l'ouverture de la parabole :

Ce contenu est protégé par le droit d'auteur. Toute reproduction à l'extérieur des forums Alloprof est interdite et pourra être considérée comme une violation du droit d'auteur.

Si a est positif, la parabole est ouverte vers le haut, tandis que si a est négatif, la parabole est ouverte vers le bas.

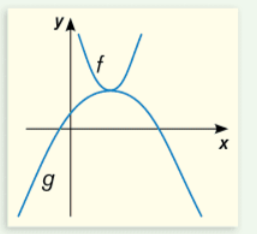
Dans ton graphique, puisque la parabole g est ouverte vers le bas, on peut déduire que son paramètre a est obligatoirement négatif, donc a<0 pour la fonction g :

Ce contenu est protégé par le droit d'auteur. Toute reproduction à l'extérieur des forums Alloprof est interdite et pourra être considérée comme une violation du droit d'auteur.

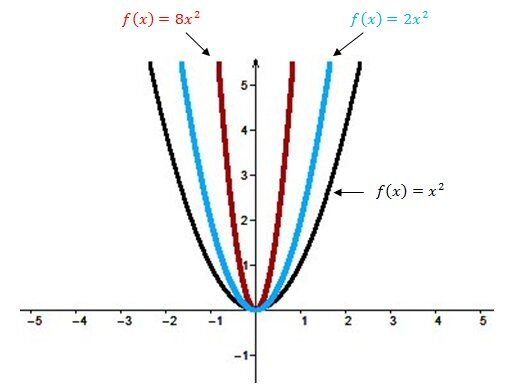
Ensuite, plus la valeur absolue du paramètre a est grand (plus le nombre sans considérer le signe est grand), plus l’ouverture de la parabole est petite :

Ce contenu est protégé par le droit d'auteur. Toute reproduction à l'extérieur des forums Alloprof est interdite et pourra être considérée comme une violation du droit d'auteur.

et moins la valeur absolue est grande, plus elle est large :

Ce contenu est protégé par le droit d'auteur. Toute reproduction à l'extérieur des forums Alloprof est interdite et pourra être considérée comme une violation du droit d'auteur.

Ce contenu est protégé par le droit d'auteur. Toute reproduction à l'extérieur des forums Alloprof est interdite et pourra être considérée comme une violation du droit d'auteur.

Dans ton graphique, on peut constater que la parabole g est plus large que la parabole f. Donc, la valeur absolue du paramètre a de g doit être plus petite que la valeur absolue du paramètre a de f. En d'autres mots : |a de g| < |a de f|

Ainsi, on doit avoir un paramètre a entre 0 et -1 ! Notre intervalle possible est ] -1, 0 [.

Si a était un nombre plus petit, comme -2 par exemple, la parabole b serait moins large que la parabole f. C'est pourquoi notre maximum est -1.

Ce contenu est protégé par le droit d'auteur. Toute reproduction à l'extérieur des forums Alloprof est interdite et pourra être considérée comme une violation du droit d'auteur.

Voici une fiche sur cette notion qui pourrait t'être utile, tu y trouveras une animation qui pourrait t'aider à mieux visualiser l'effet des différents paramètres : Le rôle des paramètres dans une fonction polynomiale de degré 2 | Secondaire | Alloprof

J'espère que c'est plus clair pour toi! :)

Salut, alors moi aussi j'avais beaucoup de difficulté avec cela jusqu'à...... l'an dernier. C'est bien que tu en maitrise déjà plusieurs, mais personnellement, je trouve que en effet, les tables de 6-7-8 sont compliqués mais j'ai 2 trucs pour le 9 :

1. Si tu utilises tes 2 mains (de gauche à droite) et que tu baisses le 1er (donc le pouce gauche), il te restes 9 doigts, ce qui équivaut à 9x1. Ensuite, si tu baisses le 2e (l'index gauche), tu peux remarquer que le doigts baissé fait comme une barriere. Donc la, tu comptes le nombre de doigts à gauche du doigt baissé. Il y en a 1. Et à droite? 8. Et si tu mets les 2 chiffres ensemble, sa fait 18, comme 9x2. Tu continues comme sa et tu auras ta table jusqu'a 9x9=81
2. Sur une feuille en papier que tu sépares en 2, tu écris à gauche les chiffres de 0 à 9 en colonne. A droite. tu fait la meme chose mais de l'autre ordre, de 9 a 0. Quand tu mets les 2 chiffres ensemble, sa donne les tables de 1 a 10.
3. Sinon, ce qui m'a le plus aidé c'était Xtra Math, tu peux choisir entre additions-soustractions ou multiplication-division et sa te donnes des calculs a faire super rapidement. Personnellement, je connais mes tables par coeur grace a ce site. Tu pourrais peut etre suggerer à ton prof d'utiliser ce site?? Bonne journée et t'inquiète, meme si sa semble impossibles, tu vas y arriver !!

Salut, 

Merci d'utiliser la zone d'entraide. 

Non, ce n'est pas des droites perpendiculaires, puisque ces dernières doivent respecter la définition suivante: "Des droites perpendiculaires sont des droites sécantes qui se coupent à angle droit, puisque la pente de l'une est l'opposé de l'inverse de la pente de l'autre." 

Les droites doivent donc se couper pour répondre au critère de perpendicularité, elles ne le sont pas si elle ne se croise pas. 

Pour en savoir plus, tu peux consulter la fiche suivante: 

À bientôt, 

Karen

Salut!

On te donne plusieurs règles : \(t=8r\), \(t=5r+5\), etc.

La variable \(t\) est le terme, et la variable \(r\) est le rang. En d'autres mots, une règle te permet de trouver le terme à un certain rang d'une suite de nombres, ou le rang d'un certain terme.

Pour trouver le terme à un certain rang \(n\), on doit remplacer la lettre n dans la règle par le rang souhaité pour trouver le terme à ce rang-là. Par exemple, voici les calculs qui nous ont permis d'obtenir les cinq premiers termes de la suite \(t=8r\) :

n=1 : \(t=8(1)=8 \)

n=2 :\(t=8(2)=16\)

n=3 : \(t=8(3)=24\)

n=4 : \(t=8(4)=32\)

n=5 : \(t=8(5)=40\)

Tu peux suivre la même démarche pour trouver les cinq premiers termes des autres suites de nombres.

Voici une fiche sur cette notion qui pourrait t'être utile, elle présente plusieurs exemples similaires : La règle d'une suite | Secondaire | Alloprof

J'espère que c'est plus clair pour toi! Si tu as d'autres questions, n'hésite pas à nous réécrire! :)