Bon matin!
Voici un problème sur le plan incliné qui me confond énormément:
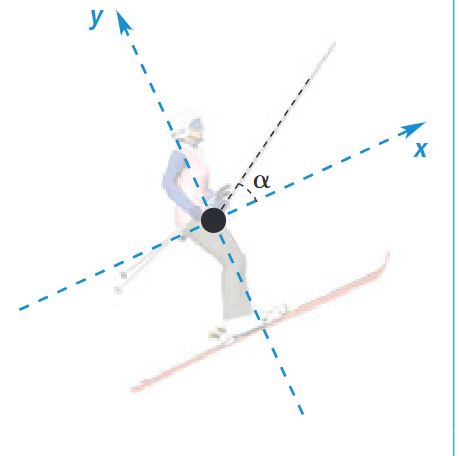
D'abord, petite confusion: en dessinant le DCL, je n'arrivais pas à comprendre comment savoir où placer mon angle têta.
Ensuite, ma grande confusion est causé par la présence simultanée de l'angle alpha et têta. Voici le corrigé:
En fait, comme on le voit surligné en jaune, Fgx nécessite l'utilisation de l'angle alpha, alors que Tx nécessite l'angle têta. Visuellement, pourquoi? Pourriez-vous m'expliquer avec des illustrations svp car je n'arrive vraiment pas à comprendre quand utiliser quel angle dans mes calculs et quelle force cible quel angle. C'est vraiment l'une de mes faiblesses dans cette matière. Auriez-vous des astuces qui m'aideront avec cette difficulté?
Puis, dans l'étape 2, pourquoi utilise-t-on le cosinus pour la composante en x de la tension?? J'arrive vraiment pas à comprendre quand utiliser sinus et quand utiliser cosinus dans mes calculs, surtout parce qu'on est dans un plan incliné, et ça me bloque beaucoup. Auriez-vous des astuces pour cela?
Je suis une personne visuelle donc ça m'aiderait énormément si vous me guidez dans vos explications détaillées avec des illustrations et graphiques, ainsi que des démonstrations mathématiques si possible! Merci beaucoup!


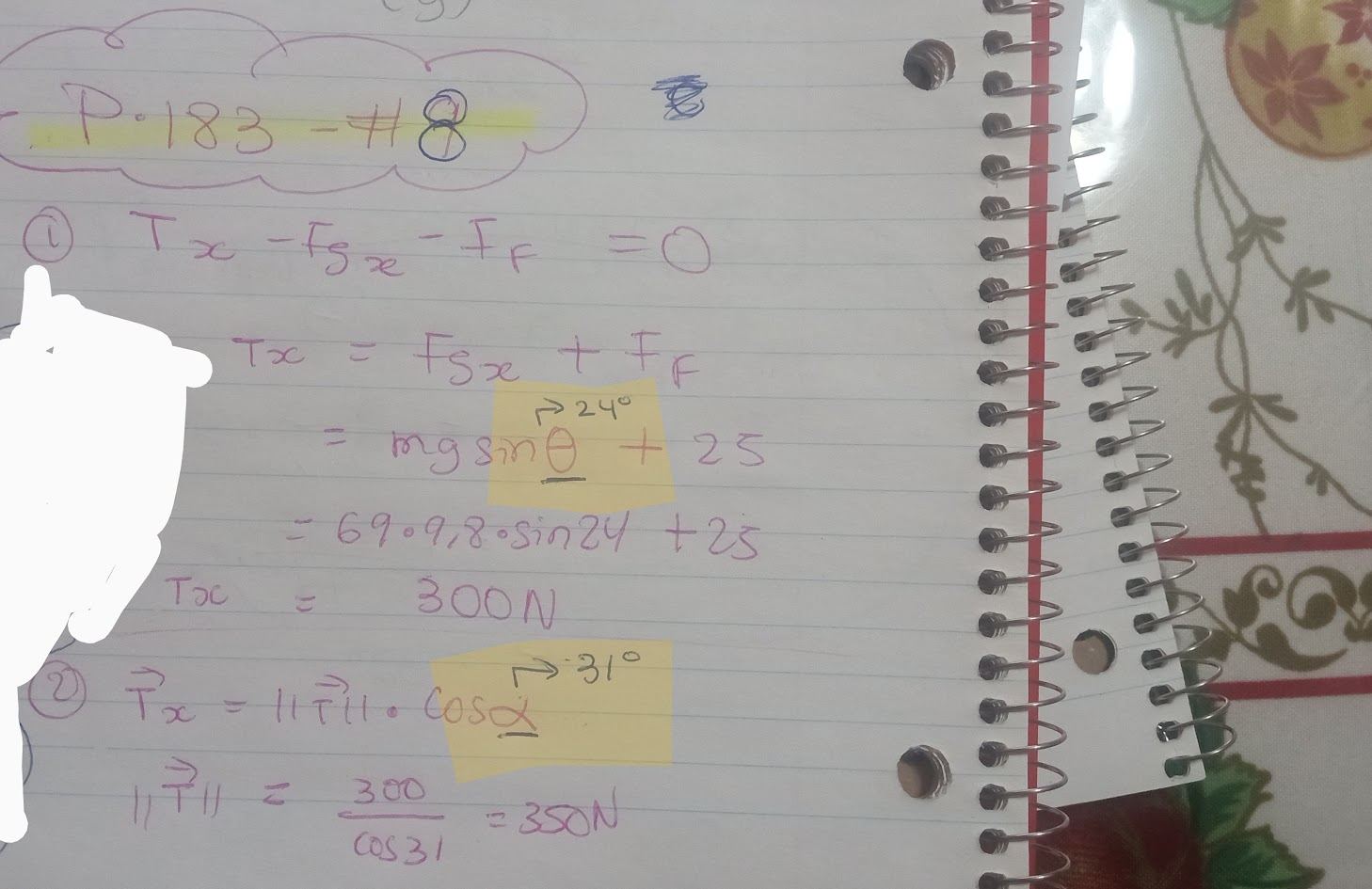






Explanation from Alloprof
This Explanation was submitted by a member of the Alloprof team.
Merci pour ta question!
Alpha et theta sont des symboles arbitraires qu'on utilise pour identifier différents angles dans un problème. Ainsi, il n'y a pas vraiment de «stratégie» pour les identifier. Cela dit, on utilise souvent theta pour faire référence à l'inclinaison des pentes, tandis que alpha est souvent utilisé pour l'orientation des forces. Je te suggère surtout de regarder le schéma (ou de le dessiner pour savoir quel angle est lequel).
Ce contenu est protégé par le droit d'auteur. Toute reproduction à l'extérieur des forums Alloprof est interdite et pourra être considérée comme une violation du droit d'auteur.
Pour ta seconde question, la raison pour laquelle on utilise différents angles est car ces angles s'appliquent à différentes forces. Par exemple, l'angle de la pente est important pour calculer la composante efficace de la gravité, tandis que l'angle de la force est important pour trouver la valeur de la force. On n'a pas besoin de tenir en compte la valeur de theta, car le diagramme est déjà tourné une fois qu'on trouve la composante en x de la force :
Ce contenu est protégé par le droit d'auteur. Toute reproduction à l'extérieur des forums Alloprof est interdite et pourra être considérée comme une violation du droit d'auteur.
Maintenant, trouvons pourquoi et quand utiliser le cosinus ou le sinus. En fait, le cosinus et le sinus sont dérivés d'un système de coordonnées dans le cercle trigonométrique :
Ce contenu est protégé par le droit d'auteur. Toute reproduction à l'extérieur des forums Alloprof est interdite et pourra être considérée comme une violation du droit d'auteur.
Il n'est pas important de comprendre comment le cercle fonctionne, mais seulement que le cos de l'angle du vecteur est égal à la distance horizontale, tandis que le sin de l'angle du vecteur est égal à la distance verticale.
En appliquant ce même principe pour les forces, on réalise qu'on peut utiliser le cos pour trouver la composante horizontale d'une force et le sin pour trouver la composante verticale d'une force.
Ce contenu est protégé par le droit d'auteur. Toute reproduction à l'extérieur des forums Alloprof est interdite et pourra être considérée comme une violation du droit d'auteur.
Par contre, attention, il faut faire attention à l'orientation de l'angle! Le cos est la composante directement adjacente à la mesure de l'angle, tandis que le sin est la composante qui n'est pas adjacente à l'angle. Ainsi, dans la situation suivante (si l'angle était mesuré par rapport à la verticale plutôt que l'horizontale), il faudrait utiliser le sin pour trouver la composante horizontale et le cos pour trouver la composante verticale :
Ce contenu est protégé par le droit d'auteur. Toute reproduction à l'extérieur des forums Alloprof est interdite et pourra être considérée comme une violation du droit d'auteur.
Voilà!
Cette fiche du site d'Alloprof explique les composantes des vecteurs :
N'hésite pas si tu as d'autres questions!