Secondary IV • 2yr.
Bonjour!
Je ne comprends pas comment résoudre cette équation à l'aide de la formule quadratique? Comment trouver mon a, b et c? Et surtout, comment trouver mes deux solutions pour cette équation? S.v.p aidez-moi!
Merci d'avance.
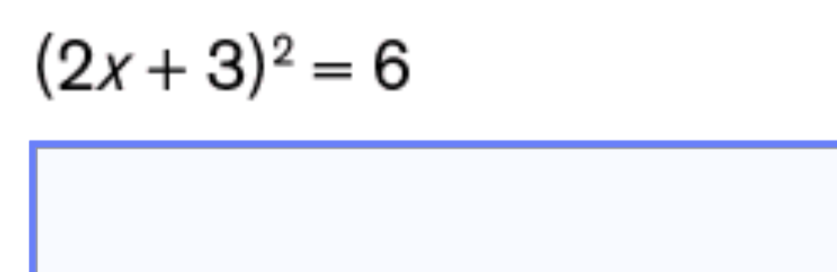






Explanation verified by Alloprof
This Explanation was verified by a member of the Alloprof team.
☺
Sous cette forme, il est plus rapide de ne pas transformer sous la forme générale.
\[ (2x+3)^2=6 \]
\[(2x+3)=\pm \sqrt{6}\]
\[2x=-3\pm \sqrt{6}\]
\[x=\frac{-3\pm \sqrt{6}}{2}\]
Note que bien que souvent une parabole aura deux solutions car elle rencontrera l'axe des x deux fois à cause de sa symétrie, il arrive
Explanation from Alloprof
This Explanation was submitted by a member of the Alloprof team.
Salut!
Pour résoudre cette équation à l'aide de la formule quadratique, tu dois d'abord transformer l'équation pour qu'elle ait la forme suivante :
Ce contenu est protégé par le droit d'auteur. Toute reproduction à l'extérieur des forums Alloprof est interdite et pourra être considérée comme une violation du droit d'auteur.
Pour cela, tu dois développer l'expression en effectuant l'exposant 2, comme ceci :
$$ (2x+3)^2 = 6$$
$$ (2x+3)(2x+3) = 6$$
$$ 4x^2+6x+6x+9 = 6$$
$$ 4x^2+12x+9 = 6$$
$$ 4x^2+12x+9 -6= 6-6$$
$$ 4x^2+12x+3= 0$$
Voilà! Maintenant qu'on a la bonne forme d'équation, on peut déduire que nos paramètres sont : a=4, b=12 et c=3.
Tu peux maintenant utiliser la formule quadratique avec ces paramètres :
Ce contenu est protégé par le droit d'auteur. Toute reproduction à l'extérieur des forums Alloprof est interdite et pourra être considérée comme une violation du droit d'auteur.
Voici une fiche sur cette notion qui pourrait t'être utile : La formule quadratique | Secondaire | Alloprof
J'espère que c'est plus clair pour toi! :)