Bonjour!
En ce moment, en physique, nous apprenons les plans inclinés, mais j'ai de grandes confusions qui me bloquent.
D'abord, je n'arrive pas à comprendre pourquoi, dans un plan incliné, le fait qu'on incline le référentiel mène à utiliser le sinus pour trouver la composante en x de la force gravitationelle et le cosinus pour son composante en y. Visuellement et mathématiquement, qu'est-ce qui expliquerait ce changement de formule? Pourquoi sinus pour x, pourquoi cosinus pour y? Pourriez-vous me la démontrer svp?
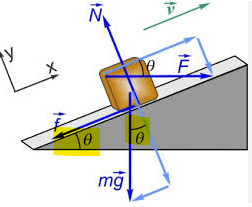
Ensuite, je n'arrive pas à démontrer et comprendre pourquoi, dans l'image ci-dessous, l'angle têta formé par le plan incliné et celui formé par les composantes de la force gravitationelle sont identiques?? Ça me confonds vraiment et je n'arrive juste pas à voir le pourquoi et le comment de ce fait.
Svp, j'ai vraiment besoin d'aide avec ces concepts vu que j'éprouve de la difficulté à les démontrer et les concrétiser :_(
Je suis une personne visuelle donc ça m'aiderait énormément si vous me guidez dans vos explications détaillées avec des illustrations et graphiques, ainsi que des démonstrations mathématiques si possible! Merci beaucoup!






Explanation from Alloprof
This Explanation was submitted by a member of the Alloprof team.
Salut!
Tout d'abord, pour mieux comprendre, imaginons que nous avons le référentiel usuel, avec l'axe des \(x\) à l'horizontale et l'axe des \(y\) à la verticale :
Ce contenu est protégé par le droit d'auteur. Toute reproduction à l'extérieur des forums Alloprof est interdite et pourra être considérée comme une violation du droit d'auteur.
Dans ce cas-là, notre poids \(m\overrightarrow{g}\) serait orienté vers l'axe négatif des y, donc elle n'aurait pas de composante en x, n'est-ce pas? Même chose pour la force de poussée \(\overrightarrow{F}\), elle serait orientée vers l'axe des \(x\), donc nous n'avons pas besoin de la décomposer, puisqu'elle n'a pas de composante en \(y\).
Cependant, il faudrait décomposer la force de frottement et la forme normale. Donc, on doit toujours décomposer une force selon les axes \(x\) et \(y\) de notre référentiel si elle n'est pas déjà parallèle à l'un des axes. Ainsi, c'est les composantes de ces forces qui seront parallèles aux axes. Par exemple, on voit dans le dessin ci-dessus que la composante en \(x\) de la force de frottement, soit \(f_{x}\), est parallèle à l'axe des \(x\), et la composante en \(y\), soit \(f_{y}\), est parallèle à l'axe des \(y\). Même chose pour la force normale, ses composantes \(N_{x}\) et \(N_{y}\) sont parallèles aux axes de notre référentiel.
Si on modifie notre référentiel en lui donnant une inclinaison par rapport à l'horizontale, le principe reste le même.
Ce contenu est protégé par le droit d'auteur. Toute reproduction à l'extérieur des forums Alloprof est interdite et pourra être considérée comme une violation du droit d'auteur.
Les forces qui sont déjà parallèles à l'un des axes, donc ici \(\overrightarrow{g}\) (qui est parallèle à l'axe des x) et \(\overrightarrow{N}\) (qui est parallèle à l'axe des y) n'ont pas besoin d'être décomposée, puisqu'elles ont une seule composante qui équivaut à la norme du vecteur et une autre composante nulle (\(N_{x}=||\overrightarrow{N}||\) et \(N_{y}\)=0, et \(f_{x}=||\overrightarrow{f}||\) et \(f_{y}\)=0).
Pour les autres forces qui ne sont pas déjà parallèles à l'un des axes du référentiel que l'on a, donc ici \(\overrightarrow{F}\) et \(m\overrightarrow{g}\), il faut les décomposer de façon à former un triangle rectangle dont les cathètes (les composantes) sont parallèles aux axes de notre référentiel! C'est pourquoi la force \(m\overrightarrow{g}\) est décomposé en \(mg_{x}\) (qui est parallèle à l'axe des x) et \(mg_{y}\) (qui est parallèle à l'axe des y)! Même chose pour \(\overrightarrow{F}\) , que l'on décompose en \(F_{x}\) et \(F_{y}\).
Maintenant, pourquoi sinus pour x, pourquoi cosinus pour y? C'est une question de trigonométrie dans le triangle rectangle! Ce n'est pas toujours sinus pour x et cosinus pour y, ça dépend de l'angle que l'on utilise! Il faut se rappeler notre truc : SohCahToa!
Ce contenu est protégé par le droit d'auteur. Toute reproduction à l'extérieur des forums Alloprof est interdite et pourra être considérée comme une violation du droit d'auteur.
Ainsi, le côté opposé à l'angle θ est \(mg_{x}\). Donc, il faut utiliser le rapport sin (SohCahToa) pour trouver la composante en x du poids. De la même façon, le côté adjacent à l'angle θ est \(mg_{y}\). Donc, il faut utiliser le rapport cos (SohCahToa) pour trouver la composante en y du poids.
Ce contenu est protégé par le droit d'auteur. Toute reproduction à l'extérieur des forums Alloprof est interdite et pourra être considérée comme une violation du droit d'auteur.
Si on voulait plutôt utiliser l'angle β suivant (qui équivaut à 180-90-θ) :
Ce contenu est protégé par le droit d'auteur. Toute reproduction à l'extérieur des forums Alloprof est interdite et pourra être considérée comme une violation du droit d'auteur.
Alors, le côté opposé à l'angle β serait \(mg_{y}\), donc il faudrait utiliser sin (SohCahToa) pour trouver la composante en y de la force. Le côté adjacent à l'angle β serait \(mg_{x}\), donc il faudrait utiliser cos (SohCahToa) pour trouver la composante en x de la force.
On voit donc qu'on doit trouver le rapport trigonométrique à utiliser selon l'angle que l'on utilise! :)
Ensuite, concernant ta seconde question, il faut utiliser nos différentes relations entre les angles pour arriver à cette conclusion. On se rappelle que notre référentiel est parallèle au plan incliné, donc son axe des x a un angle de θ par rapport à l'horizontale. Puisque la composante en x du poids est parallèle à l'axe des x, alors elle aussi possède un angle de θ par rapport à l'horizontale :
Ce contenu est protégé par le droit d'auteur. Toute reproduction à l'extérieur des forums Alloprof est interdite et pourra être considérée comme une violation du droit d'auteur.
Donc, l'angle suivant est de 90-θ:
Ce contenu est protégé par le droit d'auteur. Toute reproduction à l'extérieur des forums Alloprof est interdite et pourra être considérée comme une violation du droit d'auteur.
Donc, l'angle que tu as souligné en jaune est de 180 - 90 - (90-θ), ce qui équivaut à θ ! :
$$180 - 90 - (90-θ)$$
$$=90-(90-θ)$$
$$=90-90+θ$$
$$=θ$$
Voilà! J'espère que c'est plus clair pour toi! :)