Bon matin!
J'ai une confusion par rapport à la recherche de la règle d'une fonction sinus.
A) En fait, est-ce que le point de démarrage (h,k) est le premier point du graphique, ou bien le premier point sur l'axe d'oscillation??
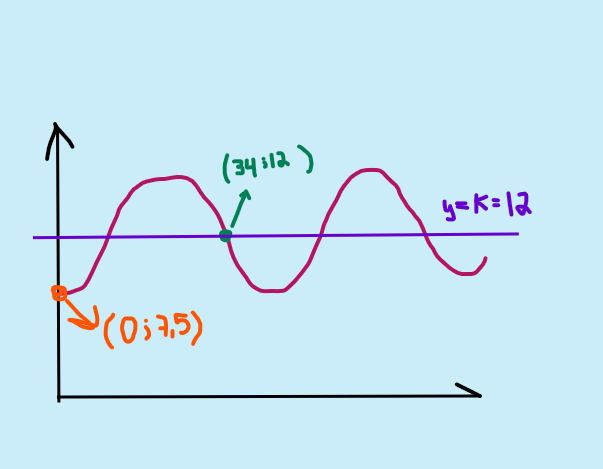
Par exemple, dans l'exemple suivant, est-ce que ce serait le point vert?
B) Ensuite, si je considère un autre point sur l'axe d'oscillation comme étant mon point de démarrage, est-ce que cela changerait mon équation? Comment et pourquoi?
C) Puis, que représente le paramètre "b" dans le fonction sinus?? Par exemple, je comprend que le "a", c'est l'amplitude de l'onde, mais quand est-il de b?
D) Finalement, que représente la période justement? Et, comment la délimiter dans un graphique??
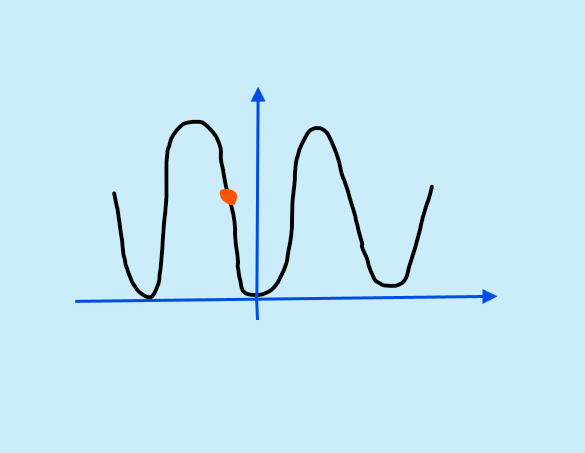
Par exemple, si je commence au point orange, où se termine la période? :
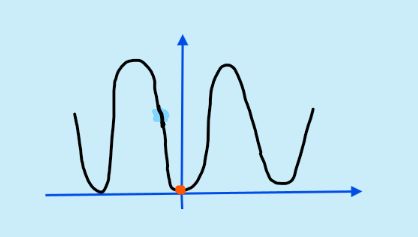
Et si je commence ici? :






Explanation from Alloprof
This Explanation was submitted by a member of the Alloprof team.
Salut!
A) Le point (h, k) est un point sur l'axe d'oscillation! Donc, c'est le point en vert, ou n'importe lequel de ces points en rouge :
Ce contenu est protégé par le droit d'auteur. Toute reproduction à l'extérieur des forums Alloprof est interdite et pourra être considérée comme une violation du droit d'auteur.
Selon le point (h, k) que tu auras choisi, tu dois ajuster les signes de tes paramètres a et b :
Ce contenu est protégé par le droit d'auteur. Toute reproduction à l'extérieur des forums Alloprof est interdite et pourra être considérée comme une violation du droit d'auteur.
Par exemple, si tu choisis le point en vert (34, 12), alors la fonction est décroissante à (h, k), donc a et b doivent être de signes contraires.
Si tu choisis plutôt ce point (h, k) :
Ce contenu est protégé par le droit d'auteur. Toute reproduction à l'extérieur des forums Alloprof est interdite et pourra être considérée comme une violation du droit d'auteur.
alors la fonction est croissante à (h, k), donc a et b doivent être de même signe.
B) Oui, comme expliqué, cela affecte les signes des paramètres a et b. Tu dois donc regarder si ton point (h, k) est sur une partie croissante de la fonction (on monte dans la courbe), ou une partie décroissante (on descend dans la courbe).
C) Le paramètre b permet de trouver la période de la fonction en utilisant cette formule :
Ce contenu est protégé par le droit d'auteur. Toute reproduction à l'extérieur des forums Alloprof est interdite et pourra être considérée comme une violation du droit d'auteur.
La période correspond à l'intervalle en x où on parcourt 1 cycle complet de la fonction (en d'autres mots, on part d'un point, on monte et on descend, ou on descend et on montre, et on revient au même point).
Par exemple, ici :
Ce contenu est protégé par le droit d'auteur. Toute reproduction à l'extérieur des forums Alloprof est interdite et pourra être considérée comme une violation du droit d'auteur.
La période est de π (π/2 - -π/2 = π/2 + π/2 = π). Donc, on calcule la valeur absolue du paramètre b comme ceci :
Ce contenu est protégé par le droit d'auteur. Toute reproduction à l'extérieur des forums Alloprof est interdite et pourra être considérée comme une violation du droit d'auteur.
D) La période correspond à l'intervalle en x où on parcourt un cycle complet de la fonction.
Dans ton premier graphique, j'ai surligné un cycle complet en vert :
Ce contenu est protégé par le droit d'auteur. Toute reproduction à l'extérieur des forums Alloprof est interdite et pourra être considérée comme une violation du droit d'auteur.
Pour trouver la période d'un cycle de la fonction, tu dois soustraire les coordonnées en x du point de départ et de fin du cycle.
Dans ton deuxième graphique, voici un cycle complet à partir du point que tu as choisi :
Ce contenu est protégé par le droit d'auteur. Toute reproduction à l'extérieur des forums Alloprof est interdite et pourra être considérée comme une violation du droit d'auteur.
Puisque le point de départ de ce cycle est un minimum, alors il est plus pratique d'évaluer la fonction avec une fonction cosinus.
Ce contenu est protégé par le droit d'auteur. Toute reproduction à l'extérieur des forums Alloprof est interdite et pourra être considérée comme une violation du droit d'auteur.
Si le point de départ du cycle est sur l'axe d'oscillation, alors la fonction sinus est plus pratique.
Ce contenu est protégé par le droit d'auteur. Toute reproduction à l'extérieur des forums Alloprof est interdite et pourra être considérée comme une violation du droit d'auteur.
Voici des fiches qui pourraient t'aider à mieux comprendre ces notions :
Voilà! J'espère que cela t'aide! :)