Matières
Niveaux
La règle d’une fonction sinus est |f(x)=a\sin\!\big(b(x-h)\big)+k.|
Le paramètre |a| est lié à l’amplitude.
Le paramètre |b| est lié à la période.
Le paramètre |h| est lié au déphasage.
Le paramètre |k| est lié à l’axe d’oscillation.
Lorsqu’on cherche la règle d’une fonction sinusoïdale à partir de la fonction sinus, on doit repérer un cycle qui débute et se termine à un point d’inflexion, c’est-à-dire un point situé sur l’axe d’oscillation. Le point au début du cycle choisi correspond au couple |(h,k).|
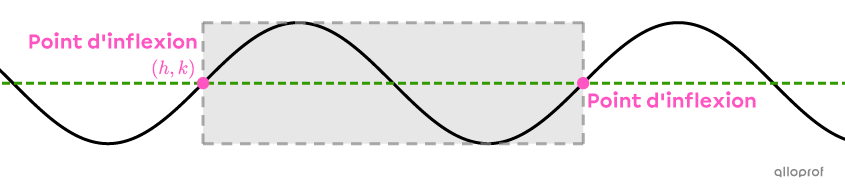
Comme il existe une infinité de points d’inflexion pour une même fonction sinus, il y a une infinité de couples |(h,k)| possibles.
Déterminer |h| et |k| à l’aide des coordonnées d’un point d’inflexion.
Délimiter un cycle à partir du point |(h,k)| choisi.
Déterminer |\vert a\vert| grâce à l’amplitude.
Déterminer |\vert b\vert| grâce à la période.
Déterminer les signes de |a| et de |b.|
Si la fonction est croissante à |(h,k)| : |a| et |b| sont de même signe.
Si la fonction est décroissante à |(h,k)| : |a| et |b| sont de signes contraires.
Écrire la règle de la fonction.
Comme on obtient la même représentation graphique lorsque |a| et |b| sont tous les deux du même signe, on peut rendre l’écriture plus simple et choisir, à l’étape 5, de les mettre positifs.
Lorsque |a| et |b| sont de signes contraires, toujours afin de rendre l’écriture plus simple, il est préférable de choisir une valeur positive à |b| et négative à |a.| De façon générale, on peut toujours attribuer une valeur positive à |b| et faire varier seulement le signe de |a.|
|a| et |b| sont de même signe ||\begin{align}a&>0\\b&>0\end{align}||
|a| et |b| sont de signes contraires ||\begin{align}a&<0\\b&>0\end{align}||
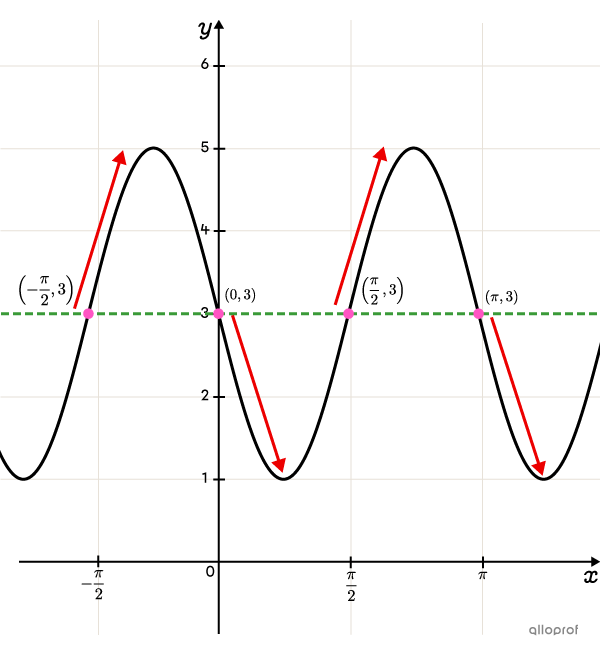
Détermine la règle de la fonction sinus représentée dans le plan cartésien suivant.

Lorsqu’on choisit un point |(h,k)| différent, on obtient une autre règle, mais qui fonctionne tout autant pour une même représentation graphique. Par contre, il faut tenir compte de la variation (croissance ou décroissance) à partir du point choisi.
Dans l’exemple précédent, en choisissant le point |\left(-\dfrac{\pi}{2},3\right),| on a obtenu les 2 règles suivantes.
|f(x)=2\sin\!\bigg(2\left(x+\frac{\pi}{2}\right)\!\bigg)+3|
ou
|f(x)=-2\sin\!\bigg(-2\left(x+\dfrac{\pi}{2}\right)\!\bigg)+3|
Si on avait plutôt choisi le point |(0,3),| le cycle aurait débuté à une décroissance, ce qui signifie que |a| et |b| auraient été de signes contraires. On aurait alors obtenu les 2 règles suivantes.
|f(x)=-2\sin\left(2x\right)+3|
ou
|f(x)=2\sin\left(-2x\right)+3|
En continuant de la même façon avec le point |\left(\dfrac{\pi}{2},3\right),| on obtient les règles suivantes.
|f(x)=2\sin\!\bigg(2\left(x-\dfrac{\pi}{2}\right)\!\bigg)+3|
ou
|f(x)=-2\sin\!\bigg(-2\left(x-\dfrac{\pi}{2}\right)\!\bigg)+3|
Si on analyse chacune de ces règles, on se rend compte que |\vert a\vert,| |\vert b\vert,| et |k| ne changent jamais. Les seules différences entre elles sont la valeur de |h| et les signes de |a| et de |b.|
Voici un exemple où les coordonnées des points d’inflexion ne sont pas directement fournies. Il faut alors procéder à un peu plus de calculs pour déterminer chaque paramètre.
Détermine la règle de la fonction sinus passant par les points |(1{,}25;-0{,}25)| et |(2{,}75;-1{,}75),| représentant respectivement un maximum et un minimum.
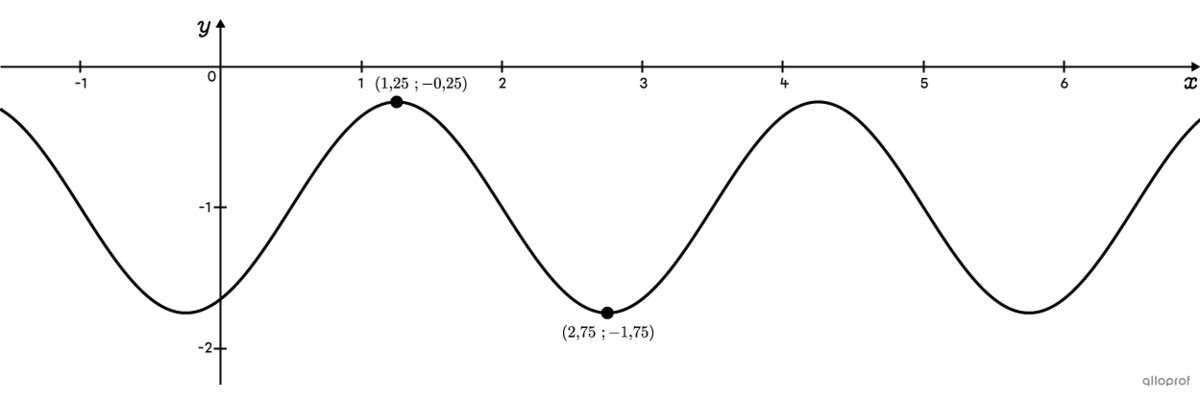
Lorsque c’est un maximum et un minimum de la fonction sinusoïdale qui sont fournis, il est plutôt avantageux de faire la recherche de la règle de la fonction cosinus. De cette façon, il y a moins de manipulations à effectuer.
Lorsqu’on demande de trouver l’équation d’une fonction sinusoïdale, on peut trouver l'équation d'une fonction sinus ou l'équation d'une fonction cosinus. Voici un exemple où l’on peut déduire l’équation d’une fonction cosinus à l’aide des identités trigonométriques.
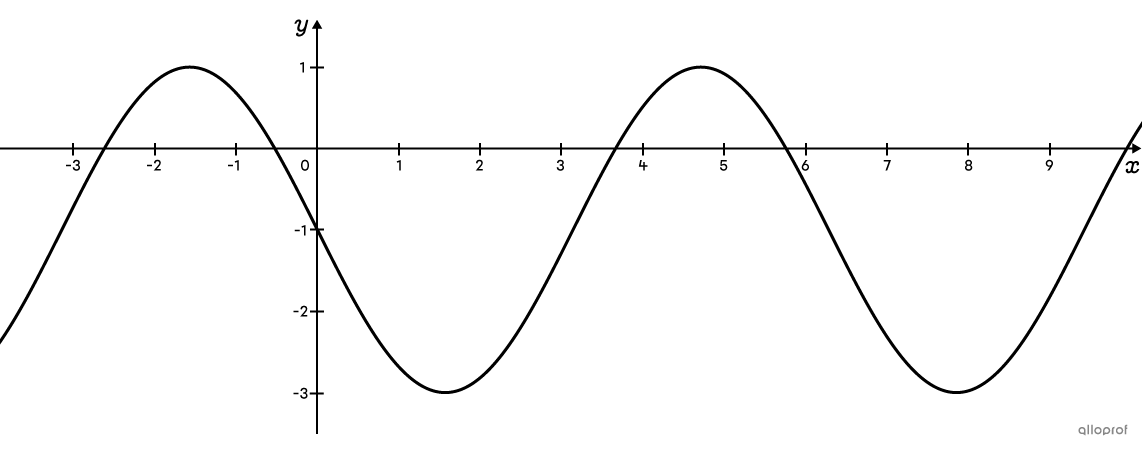
Voici une fonction sinusoïdale dont la règle, à partir de la fonction sinus, est |f(x)=-2\sin(x)-1.|
Pour transformer l’équation en fonction cosinus, on applique l’identité remarquable suivante : |\sin x=\color{#3A9A38}{\cos}\left(x\color{#3A9A38}{-\dfrac{\pi}{2}}\right).|||\begin{align}f(x)&=-2\sin(x)-1\\f(x)&=-2\color{#3A9A38}{\cos}\left(x\color{#3A9A38}{-\dfrac{\pi}{2}}\right)-1\end{align}||Les 2 règles précédentes sont équivalentes.
Remarque : Même si la règle est passée d’une fonction sinus à une fonction cosinus, |\vert a \vert| et |\vert b\vert| n’ont pas changé, puisque l’amplitude et la période sont restées les mêmes. On remarque que |k| n’a pas changé non plus étant donné que l’axe d’oscillation est aussi le même.
Les seules différences entre les règles sont la valeur de |h| ainsi que le signe de |a| et de |b.|

Moments dans la vidéo :