Populaires
Re : Question
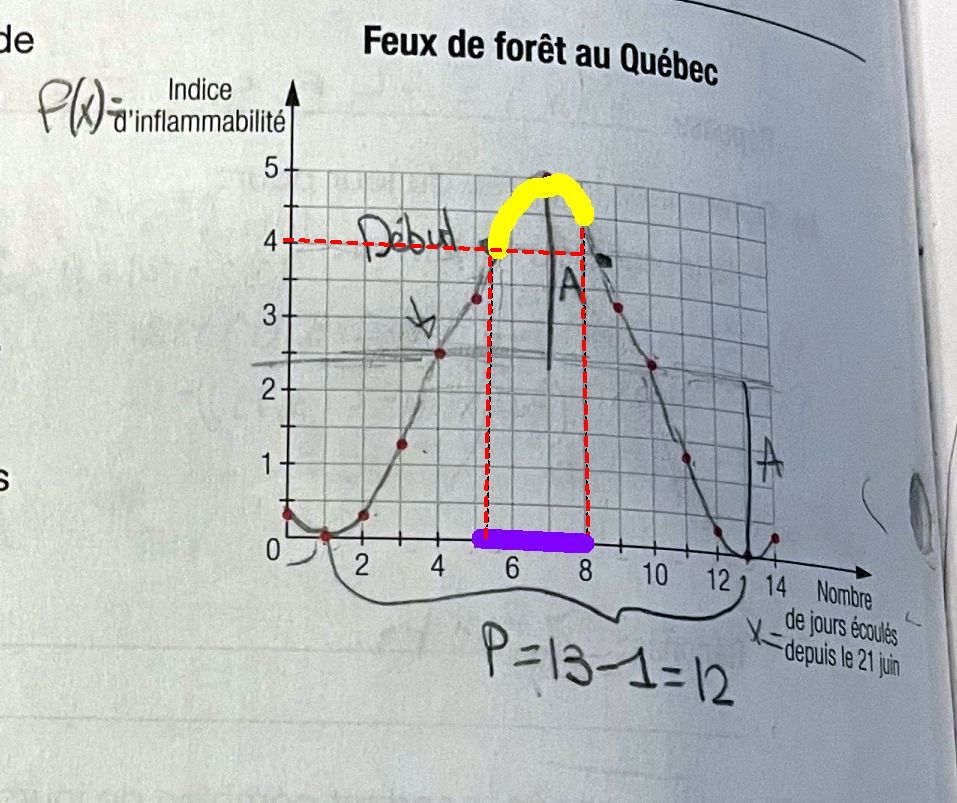
Le dernier cycle n est pas complet.
92 = 7×12 + 8.
Il faut regarder seulement les 8 premiers jours du dernier cycle.
C est pourquoi on fait 8-5,229.
Re : Question
Commence par remplacer sin x par disons z
2z² - 7z + 6 = 0
et résous pour z
ensuite tu en déduiras le x
Re : Question
Bonjour RubisFormidable465,
Merci pour ta question!
Ici, tu dois traiter cette résolution comme si tu avais des x^2. Aussi, comme on cherche entre 0 et 2pi, on veut seulement deux solutions.
Tu peux donc commencer par factoriser:
(2sinx-3)(sinx -2)=0
Ensuite, tu peux trouver les valeurs de x en isolant le x de chaque partie:
sinx=3/2
x= arcsin3/2
sinx=2
x=arcsin2
En calculant sur ta calculatrice, tu auras les réponses!
J'espère t'avoir aidé, n'hésite pas si tu as d'autres questions!
Lea-Kim
Re : Question
Non, car lorsqu'on effectue une multiplication, il faut multiplier chaque terme.
Ex: (a + b)(a + b) = a*a + a*b + b*a + b*b, qu'on peut réduire sous la forme: a^b+2ab+b^2
(* signifie la multiplication)
Ainsi, on peut d'abord développer (a+b)(a+b)(a+b) sous forme de (a^2 + 2ab + b^2)(a + b), qu'on pourra ensuite développer ainsi: a^3 + a^2b + 2a^2b + 2ab^2 + ab^2 + b^3 et qu'on pourra réduire sous la forme finale: a^3 + 3a^2b + 3 ab^2 + b^3
Re : Question
Bonsoir AvocatJaune9464!
Merci pour ta question !
Voici la démarche. Ce sont toutes des parenthèses. Commençons donc de la gauche à droite.
$$ (a+b)(a+b) $$
$$ a(a+b) + b(a+b) $$
$$ a² + 2ab + b² $$
$$ (a² + 2ab + b²)(a+b) $$
$$ a(a² + 2ab + b²) + b(a² + 2ab + b²) $$
$$ a³ + 3a²b + 3ab² + b³ $$
J'espère que tu comprennes mieux maintenant. Je te conseille de donner une attention particulière à cette fiche !
Re : Question
Salut!
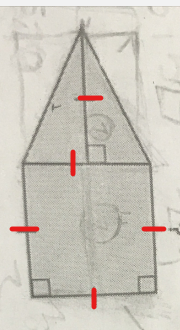
On te dit que l'aire totale est de 54 cm², et cette aire inclut l'aire du carré et l'aire du triangle, on peut donc écrire l'équation suivante :
$$ 54 = Aire_{carré} + Aire_{triangle}$$
L'aire d'un carré se trouve avec la formule A=côté², et l'aire d'un triangle avec la formule A=base × hauteur /2.
On peut donc réécrire notre équation d'aire en incluant ces deux formules, comme ceci :
$$ 54 = c^2+ \frac{b\times h}{2}$$
Lorsqu'on a des traits sur un des côtés d'une forme, cela signifie que les mesures de ces côtés sont équivalentes.
Ainsi, la hauteur du triangle est équivalente à la base du triangle et au côté du carré. On peut alors réécrire notre formule d'aire totale pour n'avoir qu'une seule variable qui représentera toutes ces mesures équivalentes :
$$ 54 = c^2+ \frac{c\times c}{2}$$
Il ne te reste plus qu'à résoudre cette équation afin de trouver c, la mesure d'un côté du carré/la mesure de la hauteur du triangle/la mesure de la base du triangle.
Bons calculs! :)
Re : Question
Bonjour AllosaureAutonome2524,
Merci pour ta question.
Premièrement, tu dois mettre en mètre les longueurs des ficelles. Ensuite, tu peux trouver quel bout de ficelles attaché ensemble donne 4,7m.
J'espère t'avoir aidé, n'hésite pas si tu as d'autres questions!
Lea-Kim
Re : Question
Bonjour Panda Rouge!
Merci de faire appel à nos services!
Dans un circuit en série, la tension totale est la somme des tensions aux différents éléments du circuit.
Ainsi,
$$ U_{totale} = U_1 + U_2 + U_3 +... $$
Comme \(U = R \cdot I\) selon la loi d'Ohm, il est aussi possible d'exprimer cette équation ainsi:
$$ R_{totale} I_{totale} = R_1\ I_1+ R_2\ I_2 + R_3\ I_3 +... $$
Comme l'intensité est la même en tout point dans un circuit en série, on peut diviser les deux côtés de l'équation par I pour obtenir la formule de la résistance équivalente:
$$ R_{totale} = R_1+ R_2 + R_3 +... $$
Dans un circuit en parallèle, l'intensité totale est la somme de l'intensité aux différents éléments du circuit.
Ainsi,
$$ I_{totale} = I_1 + I_2 + I_3 +... $$
Comme \(I= \frac{U}{R}\) selon la loi d'Ohm, il est aussi possible d'exprimer cette équation ainsi:
$$ \frac{U_{totale}}{R_{totale}} = \frac{U_{1}}{R_{1}} + \frac{U_{2}}{R_{2}}+ \frac{U_{3}}{R_{3}} +... $$
Comme l'intensité est la même en tout point dans un circuit en série, on peut diviser les deux côtés de l'équation par U pour obtenir la formule de la résistance équivalente:
$$ \frac{1}{R_{totale}} = \frac{1}{R_{1}} + \frac{1}{R_{2}}+ \frac{1}{R_{3}} +... $$
Pour réviser les résistances équivalentes, tu peux consulter la fiche explicative suivante:
Les résistances équivalentes | Secondaire | Alloprof
J'espère que cela t'aidera!
Re : Question
Bonjour Or Autonome!
Merci de faire appel à nos services!
Pour déterminer le taux de rendement d'une réaction, tu peux d'abord trouver le rendement théorique. En convertissant les masses en nombre de moles, tu pourras trouver le nombre de moles de \(Li_3N\) théorique.
Tu pourras alors convertir cette donnée en masse et comparer la masse expérimentale et la masse théorique pour trouver le pourcentage de rendement.
J'espère que cela t'aidera!
Re : Question
Bonjour MonarqueDelta7221
Merci d'avoir posé ta question sur la zone d'entraide.
En effet, certains verbes en anglais ne suivent pas la règle du ''-ed'' au Simple Past (Passé simple) et au Past Participle (Participe passé). Un bon truc serait de lire des articles ou livres en anglais qui t'intéressent et tu pourra les identifier plus facilement.
Voici un article qui pourra t'aider avec une liste de tous ces verbes.
https://www.alloprof.qc.ca/fr/eleves/bv/anglais/irregular-verbs-0-a2411
Bonne étude!
MentheGamma6787