Populaires
Re : Question
Salut!
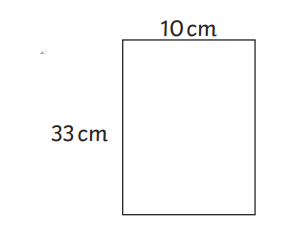
Les dimensions d'une forme représentent les mesures des côtés de cette forme. Par exemple, les dimensions de ce rectangle sont de 10 cm par 33 cm.
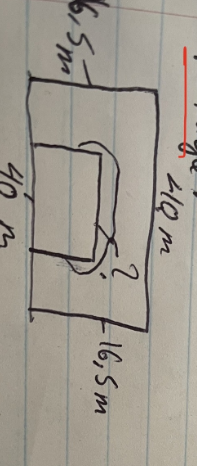
Dans ton cas, on te donne un grand rectangle dont les dimensions sont de 40 m par 16,5 m.
On te dit aussi que les dimensions du petit rectangle sont 5 fois plus petites que celles du grand rectangle. En d'autres mots, chaque mesure du petit rectangle est 5 fois plus petite que la mesure homologue du grand rectangle. (des côtés homologues = des paires de côtés proportionnels, donc la largeur du grand rectangle est homologue à la largeur du petit rectangle, et la longueur du grand rectangle est homologue à la longueur du petit rectangle).
Donc, tu dois simplement diviser les mesures du grand rectangle par 5 pour obtenir les mesures du petit rectangle.
J'espère que c'est plus clair pour toi! :)
Re : Question
y = ax² + bx + c est la forme de ta parabole
Tu n'as qu'une équation à déterminer: tu dois établir les valeurs de a, b, et c
Tu connais 3 points qui satisfont cette équation puisqu'ils sont sur la parabole, soient (0,33), (2,-27) et (8,-63)
33 = a·0 + b·0 + c => c = 33
-27 = a·2² + b·2 + 33 => (-60 - 4a)/2 = b
-63 = a·8² + b·8 + 33
-63 = 64a + 8·(-60 - 4a)/2 + 33
Tu peux donc déterminer a et b et finalement les zéros de cette parabole
Re : Question
Salut!
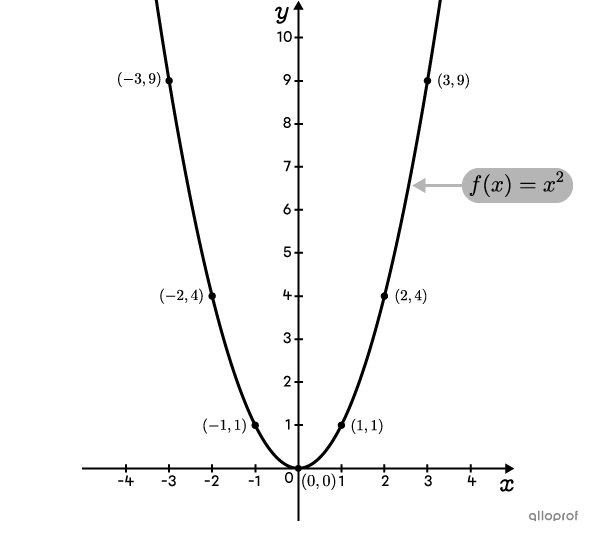
Une parabole est la représentation graphique d'une fonction polynomiale de degré 2. (un peu comme la droite est la représentation graphique d'une fonction linéaire)
Je t'invite à consulter la fiche suivante pour plus de détails : La fonction polynomiale de degré 2 | Secondaire | Alloprof
Bonne fin de soirée! :)
Re : Question
Merci pour ta question!
D'abord, l'expression de la constante d'équilibre pour la réaction suivante...
$$ aA + bB \rightleftharpoons cC + dD $$
...est la suivante :
$$ K_{c}=\displaystyle \frac{\left[C\right]^{c}\cdot\left[D\right]^{d}}{\left[A\right]^{a}\cdot\left[B\right]^{b}} $$
Ainsi, essentiellement la formule se résume à la proportion de produits par rapport aux réactifs :
$$ K_c = \frac{[produits]}{[réactifs]} $$
Bref, plus la constante est grande, plus il y aura de produits à l'équilibre.
Dans ce numéro, la plus grande constante est en c) (0,025). Ensuite, b) est la deuxième plus grande, puis c). Ainsi, je pense que ta réponse initiale était bonne, et qu'il y a une petite coquille dans le corrigé de ton manuel. La bonne réponse est donc a), b), c).
Cette fiche du site d'Alloprof explique la constante d'équilibre :
N'hésite pas si tu as d'autres questions!
Re : Question
Salut! Pour trouver le nombre N de diagonales, il faut utiliser la formule suivante: N = n(n-3)/2. (La seul exception est le triangle, qui n'a pas de diagonales.)
Il s'agit d'une équation algébrique. J'ai trouvé une fiche sur Alloprof qui pourrait t'aider:
J'espère que j'ai pu te venir en aide!
Re : Question
La formule est D = n(n-3)/2 où n est le nombre de côtés du polygone.
Un exemple:
Le nombre de diagonales d un heptagone.
ici n = 7.
donc D = 7(7-3)/2 = 7×4/2 = 14
Un heptagone possède 14 diagonales.
Re : Question
Bonjour!
Selon le type de subordonnée, la façon de faire ne sera pas la même. :)
Pour la subordonnée relative, je te suggère de la déconstruire en P1 et P2. Voici un exemple :
La maison que j'ai achetée est blanche.
P1 La maison est blanche.
P2 J'ai acheté la maison.
Tu dois te souvenir que les subordonnées sont des phrases complètes enchâssées dans d'autres phrase. Je te suggère donc d'analyser les subordonnées comme on analyse une phrase.
Je te suggère de consulter la fiche ci-dessous, elle contient les liens vers toutes nos fiches sur les différents types de subordonnées. :D
Si tu as d'autres questions, n'hésite pas à nous réécrire. Nous te répondrons avec plaisir!
Laurie :)
Re : Question
Bonjour GalaxieLucide,
Merci pour ta question!
La gamme de fabrication est un document qui décrit, de façon détaillée, toute l’information technique nécessaire à la fabrication d’une pièce ou de l’ensemble des pièces d’un objet technique.
La gamme d’assemblage est plutôt un document qui décrit l’ordre et les techniques d’assemblage ainsi que les organes de liaison à utiliser pour joindre toutes les pièces de l’objet.
Cette fiche explique en détails chacune de ces deux gammes:
N'hésite pas si tu as encore besoin d'aide:)
Kylan
Re : Question
Bonjour!
La meilleure technique d'étude peut varier selon les gens. Ce qui fonctionne pour une personne peut ne pas fonctionner pour une autre!
Je te suggère donc d'essayer plusieurs méthodes et de choisir celle qui te convient le mieux.
Tu peux, par exemple, écrire des questions et des réponses sur un papier et demander à quelqu'un de te poser les questions.
Tu peux aussi faire semblant d'être un professeur et faire comme si tu donnais une cours sur la matière.
Je te suggère aussi de consulter la fiche ci-dessous. Elle contient des trucs pour mieux étudier! :D
Si tu as d'autres questions, n'hésite pas à nous réécrire. Nous te répondrons avec plaisir!
Laurie :)
Re : Question
C'est difficile de te donner des explications car cela dépend du type d'inéquations.
Tu mentionnes la factorisation donc je présume que tu as des variables de degré 2 dans ton inéquation, possiblement une parabole.
Dans une égalité comme dans une inégalité, pour simplifier ou regrouper des variables de même type il est important de se rappeler que si on ajoute/soustrait/multiplie/divise par une valeur d'un côté, il faut le faire aussi de l'autre.
La différence entre l'égalité et l'inégalité est que dans ce dernier cas si tu multiplie ou divise par un nombre négatif, ça change l'orientation de ton inégalité.
Consulte ce site pour plus de renseignements: