Populaires
Re : Question
Salut, PoutineInoubliable6121! :D
Merci d'utiliser la Zone!
Ça fait quelques fois que tu nous envoies ce sondage, j'espère bien que tu obtiens toutes les réponses que tu souhaites! :)
Je vais te remettre ici tes anciennes publications avec les réponses de plusieurs participants si tu ne les avais pas pris en note:
Comme notre collègue CielFantastique1521 te l'a proposé, je te conseille également d'essayer de créer un sondage par Google Forms et de l'envoyer à tes amis et ta famille si tu souhaites obtenir encore plus de réponses!
Bonne rédaction et à bientôt sur la Zone!
Iris
Re : Question
Pour réparer un vélo avec une pompe électrique (compresseur portatif), retirez le capuchon de valve, fixez l'embout de la pompe (Schrader/Presta), réglez la pression cible sur l'appareil et lancez le gonflage jusqu'à l'arrêt automatique. Pour un vélo type Riverside/VTC, la pression recommandée est généralement comprise entre 3 et 5.5 bars ( ou 45-80 PSI ) pour un bon rendement
Merci pour ton message et bon travail pour la suite
Teana-Rose
Re : Question
Salut!
Un angle de 180 degrés s'appelle un angle plat.
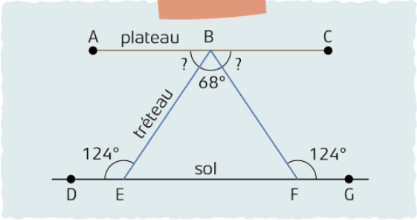
( L'affirmation : m < ABE = 56° et m < CBF = 56° ) ( La justification : Tel angle est supplémentaire donc on le divise par 2 ) Calcul : 180° - 68° = 112° et 112°/2 = 56°
Tes calculs sont les bons, bravo! Maintenant, pour remplir ton tableau, tu dois :
- affirmer que les angles ABE, EBF et CBF forment un angle plat (donc de 180 degrés), puisqu'ils sont alignés sur la droite AC
- affirmer que EBF = 68 degrés
- affirmer que ABE et CBF sont isométriques
- affirmer que ABE = 56 degrés car (180-68)/2 = 56
- même chose pour CBE, il faut affirmer qu'il est de 56 degrés avec la même justification
Une façon alternative de résoudre cet exercice est d'affirmer que les droites AC et DG sont parallèles (par hypothèse), puis que les angles DEB et CBE sont isométriques, puisqu'ils sont alternes-internes. Ensuite, on peut affirmer que CBF = 124-68 = 56 degrés.
J'espère que cela t'aide! Si tu as d'autres questions, n'hésite pas à nous réécrire! :)
Re : Question
Salut,
Merci de nous faire confiance.
C'est difficile de te répondre précisément sans avoir l'ensemble de ton portrait scolaire, connaitre le programme dans lequel tu veux aller au Cégep, etc.
Pour avoir une idée précise, je t'encourage à discuter avec la conseillère en orientation de ton école ou du cégep où tu aimerais aller. Je suis certaines qu'elles pourront t'aider à connaitre tes options.
Je te suggère aussi de ne pas te décourager, la dernière étape est celle qui vaut le plus dans le bulletin, donc tu as le temps encore de te reprendre.
N'hésite pas à nous utiliser, nous sommes là pour toi!
Karen
Re : Question
Salut !
Il semble s'agir d'un mélange entre les relations entres les angles et les propriétés des triangles.
Les relations entre les angles :
Les propriétés des triangles :
Par exemple, dans le premier exercice, tu peux compléter plusieurs des angles formés par les lignes. Pour ce faire, tu sais que la somme des angles interne d'un triangle est de 180 degrés.
À partir de là, tu peux déduire plusieurs angles. Et en ajoutant à cela les relations entres les angles, tu peux compléter le schéma au complet.
Je te laisse essayer un peu par toi-même.
J'espère que cela ait pu t'aider et si tu as d'autres questions, n'hésite pas !
Bonne soirée !
Re : Question
Salut!
La priorité des opérations est un ordre d'opérations à suivre lorsqu'on veut manipuler une chaîne d'opération.
PEMDAS est un truc mnémotechnique pour se souvenir de l'ordre que nous devons suivre dans une chaîne d'opérations.
P : Parenthèses
E : Exposants
MD : Multiplication et Division
AS : Addition et soustraction
Selon ce truc, la première chose à calculer est ce qui est entre parenthèses, suivi des exposants. Ensuite, on doit calculer les multiplications et les divisions dans l'ordre où elles apparaissent (de gauche à droite). Enfin, on calcule les additions et les soustractions dans l'ordre dans lequel elles apparaissent aussi (de gauche à droite).
Voici un petit exemple :
(5 × 2 − 3 + 10) + 32 − (10 ÷ 5 × 2) − 1 + 22
Commençons par résoudre ce qui est entre parenthèses (en respectant PEMDAS) :
(5 × 2 - 3 + 10) + 32 − (10 ÷ 5 × 2) − 1 + 22
On effectue d'abord la multiplication de 5 par 2. Ensuite, nous faisons la soustraction, car elle vient avant l'addition.
= (10 -3 + 10) + 32 − (10 ÷ 5 × 2) − 1 + 22
= (10 - 3 + 10) + 32 − (10 ÷ 5 × 2) − 1 + 22
= (7 + 10) + 32 − (10 ÷ 5 × 2) − 1 + 22
= (17) + 32− (10 ÷ 5 × 2) − 1 + 22
On fait la même chose pour la seconde parenthèse :
17 + 32 − (10 ÷ 5 × 2) − 1 + 22
Nous effectuons d'abord la division de 10 par 5, car elle vient avant la multiplication.
17 + 32 − (2 × 2) − 1 + 22
17 + 32 − (4) − 1 + 22
Terminons par les additions et les soustractions dans l'ordre dans lequel elles apparaissent (de gauche à droite) :
17 + 32 − 4 − 1 + 22 = 66
Voici une fiche sur cette notion qui pourrait t'être utile : La priorité des opérations | Secondaire | Alloprof
J'espère que c'est plus clair pour toi! :)
Re : Question
Salut, OrioleRose4460! :D
C'est une excellente question, merci d'utiliser la ZE!
Pour un texte de cette grandeur, l'introduction pourra avoir à peu près 50-75 mots. Les paragraphes de développement, eux, si on considère que tu en rédiges 2, pourront tourner à l'entour de 150-200 mots chacun. Enfin, ta conclusion aura elle aussi environ 50-75 mots.
Voici nos fiches sur la structure du texte argumentatif:
- L'introduction d'un texte argumentatif
- Le développement d'un texte argumentatif
- La conclusion d'un texte argumentatif
J'espère que cela répond à ta question ! N'hésite pas à nous réécrire si tu en as d'autres. :)
Iris
Re : Question
Salut AraResponsable3651 😊,
Merci d'utiliser la zone d'entraide pour poser tes questions!
En effet, manquer un cours peut être stressant surtout si tu as manqué de la matière qui se retrouvera dans un examen. Je vais t'aider à décortiquer cette notion, pas à pas.
Les propriétés caractéristiques sont des propriétés qui permettent de différencier une substance ou un groupe de substances, car elles sont propres à chaque matériau précis. Parmi elles, on retrouve des exemples bien connus comme la température d’ébullition, la masse volumique ou la conductivité électrique. Par exemple, si l’on cherche un objet dont la température d’ébullition est de 100 °C, on peut identifier qu’il s’agit de l’eau, puisque cette valeur est propre à ce matériau dans des conditions normales de pression. Les propriétés caractéristiques sont donc des concepts spécifiques et uniques qui permettent de reconnaître et distinguer différents matériaux.
Les propriétés non caractéristiques sont des propriétés qui ne sont pas propres à une substance. Autrement dit, elles ne permettent pas d’identifier un matériau, car elles peuvent varier selon les circonstances ou être communes à plusieurs matériaux. Parmi les exemples les plus fréquents, on retrouve la masse, le volume ou la forme d’un objet. Ces propriétés ne permettent donc pas de distinguer un matériau d’un autre. Par exemple, avoir 5 g d’un objet ne suffit pas à identifier de quoi il s’agit : cela peut être 5 g de farine, 5 g de fer ou 5 g d’eau, et la seule connaissance de la masse ne permet pas de reconnaître le matériau. Ce sont des concepts généraux et vagues qui peuvent décrire presque n’importe quel matériau ou objet.
Voici une métaphore que j'aime bien utiliser pour faire la différence : Une propriété caractéristique, c'est comme tes empreintes digitales. Chaque personne en a des différentes ce qui permet de nous différencier tous les uns des autres. Une propriété non caractéristique, c'est comme les vêtements qu'on porte. Je peux porter le même chandail qu'une autre personne, ce qui ne permet pas de nous différencier!
Sur cette fiche, tu peux cliquer sur les différentes propriétés et tu seras rediriger vers une définition plus précise de celles-ci! Ainsi, tu pourras mieux comprendre chacune des propriétés présentées dans ton tableau!
N'hésite pas si tu as d'autres questions! J'ai confiance en toi pour ton mini-test de ce lundi!