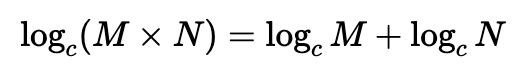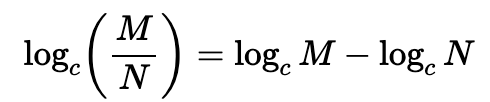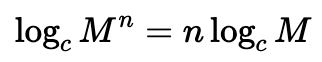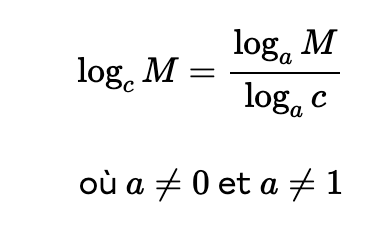Populaires

Bonsoir R2D2Noble7199 😊

Avant d'isoler ton x, tu devras diviser ton équation par -1 des deux côtés.

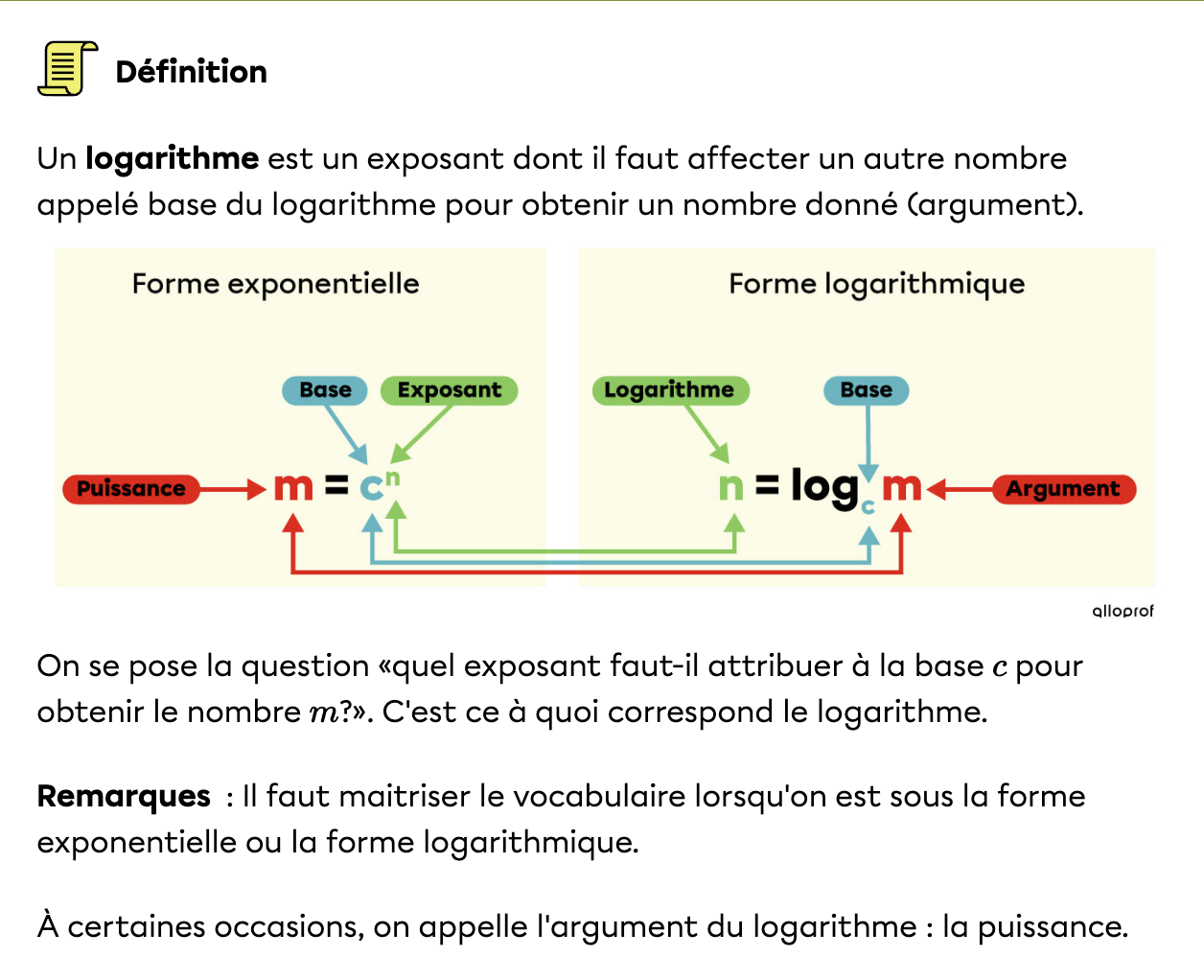
Ensuite, lorsque ton x se situe dans ton exposant, il faut utiliser la transformation en forme logarithmique.

Ce contenu est protégé par le droit d'auteur. Toute reproduction à l'extérieur des forums Alloprof est interdite et pourra être considérée comme une violation du droit d'auteur.

Ainsi, tu obtiens donc que:

$$4+x=\log_{\frac{2}{3}}\left(\frac{1}{2}\right)$$

Il ne te reste qu'à isoler ton x et calculer la réponse à l'aide de ta calculatrice.

Bonne soirée :)

Mélodie 🎶

C'est une règle de 3 (produit en croix/des extrêmes)

2π radians correspond à 360º

3π/20 radians correspond à z degrés

2π -> 360º

3π/20 -> z (inconnu)

la formule est z = (3π/20) x 360 / 2π = 27º

Plus généralement (pas seulement pour convertir des radians en degrés)

pour

A -> B

C -> z (inconnu)

z = C x B /A

Note que A et C doivent avoir la même unité de mesure alors que B et z ont la même unité de mesure.

Bonsoir OrioleRose4460,

Pour répondre à ta question, je te conseillerai de faire des fractions équivalentes en utilisant l'égalité : $$\pi=180^{\circ}$$

Tu peux écrire:

$$\frac{\pi}{(\frac{3\pi}{20})}=\frac{180^{\circ}}{?}$$

En faisant ton produit croisé, tu obtiendras l'équivalent de cet angle en degrés.

Bonsoir MercureNoble8033 😊

Ne t'en fait pas, les logarithmes sont assez difficiles à comprendre au début!

Premièrement, la constante e = 2,718 281 828 est la base des logarithmes naturels. Elle se nomme le nombre d'Euler. Au lieu d'écrire $$log_e$$, on écrit ln.

Ainsi, e représente simplement un nombre qui ne change jamais, c'est-à-dire une constante.

Le logarithme en base e est appelé logarithme naturel ou logarithme népérien.

Pour ce qui est de ton numéro, ce que ton enseignant veut, c'est que tu utilises les différentes propriétés des logarithmes pour trouver la réponse finale.

Si l'argument du logarithme est une multiplication de 2 facteurs, on obtient alors l'addition de 2 expressions logarithmiques.

Ce contenu est protégé par le droit d'auteur. Toute reproduction à l'extérieur des forums Alloprof est interdite et pourra être considérée comme une violation du droit d'auteur.

Si l'argument du logarithme est une division de 2 termes, on obtient alors une soustraction de 2 expressions logarithmiques.

Ce contenu est protégé par le droit d'auteur. Toute reproduction à l'extérieur des forums Alloprof est interdite et pourra être considérée comme une violation du droit d'auteur.

Lorsque l'argument d'un logarithme est une puissance, l’exposant peut être transformé en coefficient du même logarithme.

Ce contenu est protégé par le droit d'auteur. Toute reproduction à l'extérieur des forums Alloprof est interdite et pourra être considérée comme une violation du droit d'auteur.

Le calcul du logarithme d'un argument est équivalent au quotient du logarithme de ce même argument et du logarithme de sa base, à condition que les bases soient identiques.

Ce contenu est protégé par le droit d'auteur. Toute reproduction à l'extérieur des forums Alloprof est interdite et pourra être considérée comme une violation du droit d'auteur.

Je t'invite à consulter cette fiche contenant les différentes propriétés des logarithmes :

En manipulant ton expression, tu devrais être capable de la simplifier et de trouver le résultat sans avoir recours à ta calculatrice :)

Si jamais tu as d'autres questions, n'hésite surtout pas!

Mélodie 🎶

Note que pour ta deuxième question on veut surtout savoir si l'égalité est vraie ou fausse; ce que tu peux démontrer comme R2D2Turbo l'indique en utilisant les propriétés des logarithmes.

Pour se simplifier le travail, on multiplie l'expression de part et d'autre du signe égale par (log_2 (3) + log_2 (2)) ce qui donne

log_2 (4) + log_2 (9) = 2(log_2 (3) + log_2 (2))

log_2 (4) + log_2 (9) = 2log_2 (3) + 2log_2 (2)

or log_2 (4) = log_2 (2²) = = 2log_2 (2)

et log_2 (9) = log_2 (3²) = = 2log_2 (3)

de par le logarithme d'une puissance,

l'égalité devient donc

2log_2 (2) + 2log_2 (3) = 2log_2 (3) + 2log_2 (2)

deux sommes qui sont égales, l'énoncé est donc vrai

Il faut d'abord effectuer les opérations comme la multiplication d'une parenthèse

3/4(2x - 5/3) = 3/4 · 2x - 3/4 · 5/3 = 3x/2 - 5/4

puis tu regroupes les termes semblables (les termes en x et les constantes)

finalement tu isoles le x