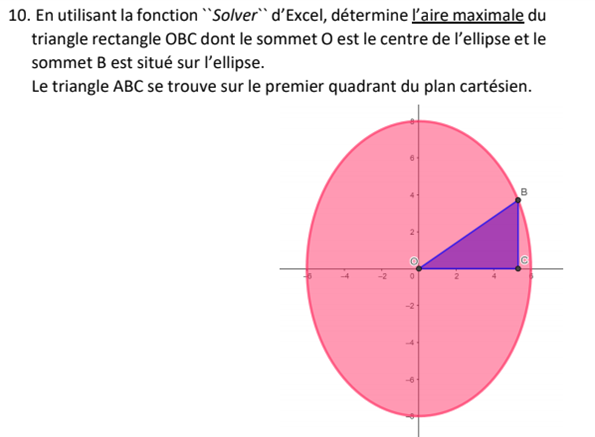
Ce contenu est protégé par le droit d'auteur. Toute reproduction à l'extérieur des forums Alloprof est interdite et pourra être considérée comme une violation du droit d'auteur.
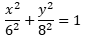
Ce contenu est protégé par le droit d'auteur. Toute reproduction à l'extérieur des forums Alloprof est interdite et pourra être considérée comme une violation du droit d'auteur.
Pouvez-vous m'aider a résoudre
Salut !
Je sais que ça n'utilise pas le solver, mais ce que j'explique ici https://www.alloprof.qc.ca/zonedentraide/discussion/2612/question peut être appliqué pour trouver la réponse sans outil technologique. Tu pourras vérifier si ce que tu fais dans le solver concorde. (Désolé s'il y a eu confusion plus tôt concernant le Desmos).
Dans le cercle unité, le plus grand triangle rectangle possible est le triangle rectangle isocèle. Tu vois pourquoi ?
Ce contenu est protégé par le droit d'auteur. Toute reproduction à l'extérieur des forums Alloprof est interdite et pourra être considérée comme une violation du droit d'auteur.
Les deux cathètes mesurent \(\displaystyle \frac{\sqrt{2}}{2}\). Son aire est \[\left(\frac{\sqrt{2}}{2} \times \frac{\sqrt{2}}{2}\right) \div 2 = \frac{1}{4}\]Si tu effectues un changement d'échelle horizontal de \(a = 6\) et un changement d'échelle verticale de \(b = 8\), tu obtiens une nouvelle aire de \[\frac{1}{4} \times 6 \times 8 = 12\]C'est ce que tu devrais obtenir avec le solver.
Ce contenu est protégé par le droit d'auteur. Toute reproduction à l'extérieur des forums Alloprof est interdite et pourra être considérée comme une violation du droit d'auteur.
Comme les cathètes sont horizontales et verticales, c'est facile de calculer leurs nouvelles mesures si tu préfères : \(\frac{\sqrt{2}}{2}\times 6 = 3\sqrt{2}\) et \(\frac{\sqrt{2}}{2}\times 8 = 4\sqrt{2}\). Tu calcules ensuite l'aire du triangle comme d'habitude \[\frac{3\sqrt{2}\times 4\sqrt{2}}{2} = \frac{24}{2} = 12\]
Au secondaire, il faut un outil technologique pour résoudre ce problème car on ne connait pas la notion de dérivée.
Explication d'Alloprof
Cette explication a été donnée par un membre de l'équipe d'Alloprof.
Salut !
Pour répondre à ta question, il faudra utiliser des concepts mathématiques et plusieurs fiches sont disponibles pour les sujets :
Avant d'utiliser solver, il te faut identifier les contraintes. Il te faut les valeurs \(x\) et \(y\) pour lesquelles l'aire du triangle est maximale :
\[Aire=_{max}\frac{h\times b}{2}=_{max}\frac{x\times y}{2}\]
La première contrainte est la formule pour l'ellipse et la deuxième est l'aire du triangle. Il faut trouver alors des valeurs pour \(x\) et \(y\) tel que l'aire est maximale et que les deux valeurs sont conformes à la formule de l'ellipse !
J'espère que cela a pu t'aider et si tu as d'autres questions, n'hésite pas !
Suggestions en lien avec la question
Suggestion en lien avec la question
Voici ce qui a été trouvé automatiquement sur le site, en espérant que ça t’aide!