Matières
Niveaux
Le périmètre et l'aire des figures planes
Fiche | Mathématiques
Secondaire
1-2
Lorsqu'on cherche la longueur du contour ou la mesure de la surface d'une figure plane, on peut se référer à différentes formules. Cependant, il faut s'assurer de bien distinguer les notions de périmètre et d'aire.
Le périmètre
Qu’une figure plane soit formée de lignes brisées ou courbes, il est possible de calculer la longueur totale des lignes qui forment son contour.
Le périmètre, généralement noté |P,| est la mesure du contour d’une figure. Pour le calculer, on additionne les mesures de tous les côtés. Dans le cas du cercle, la mesure du contour se nomme la circonférence et se note |C.|
On exprime le périmètre à l'aide d'unités de mesure à une dimension comme les |cm| et les |m.|
Pour déterminer la longueur totale de clôture dont on a besoin pour cet enclos, il faut mesurer la longueur de la ligne brisée qui forme son contour. Il s’agit donc de calculer un périmètre.
L'aire
Alors que le périmètre concerne le contour d'un figure, l'aire, quant à elle, se rapporte à la mesure de sa surface.
L’aire, généralement notée |A,| est la mesure de la surface délimitée par une figure plane.
On exprime l'aire à l'aide d'unités de mesure à 2 dimensions comme les |cm^2| et les |m^2.|
Pour déterminer le prix de ce terrain, il faut commencer par calculer son aire, soit la mesure de la superficie à l'intérieur des limites du terrain.
Pour valider ta compréhension de l'aire et du périmètre des figures planes de façon interactive, consulte la MiniRécup suivante :
Pour valider ta compréhension des mesures manquantes dans les figures planes de façon interactive, consulte plutôt la MiniRécup suivante :
Tableau résumé des formules de périmètre et d'aire
Que ce soit pour calculer la mesure du périmètre ou de l'aire, on peut utiliser différentes formules.
|
Figure plane |
Périmètre |
Aire |
|---|---|---|
 |
|P=\color{#3A9A38}{a}+\color{#3B87CD}{b}+\color{#FF55C3}{c}| |
|A=\dfrac{\color{#3B87CD}{b}\times\color{#EC0000}{h}}{2}| |
 |
|\begin{align} |
|\begin{align} |
 |
|\begin{align} |
|A=\color{#3B87CD}{b}\times\color{#EC0000}{h}| |
 |
|\begin{align} |
|A=\color{#3B87CD}{b}\times\color{#EC0000}{h}| |
 |
|\begin{align} |
|A=\dfrac{\color{#FF55C3}{D}\times\color{#3B87CD}{d}}{2}| |
 |
|P=\color{#3B87CD}{b}+\color{#3A9A38}{a}+\color{#FA7921}{B}+\color{#FF55C3}{c}| |
|A=\dfrac{(\color{#3B87CD}{b}+\color{#FA7921}{B})\times\color{#EC0000}{h}}{2}| |
 |
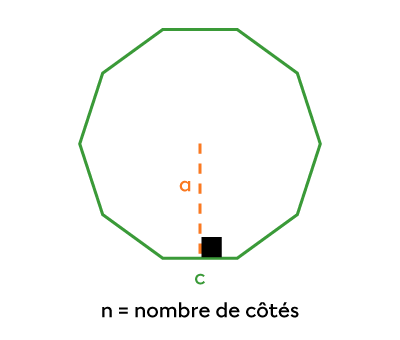|P=n\times\color{#3A9A38}{c}| |
|A=\dfrac{\color{#3A9A38}{c}\color{#FA7921}{a}n}{2}| |
 |
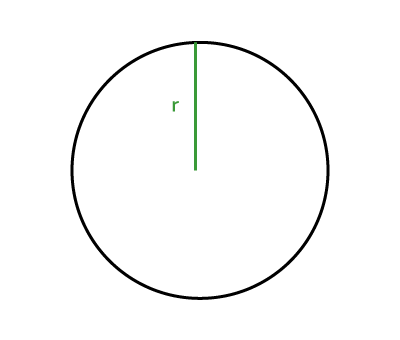|C=2\pi\color{#3A9A38}{r}| |
|A=\pi\color{#3A9A38}{r}^2| |
Vidéo
L'aire des quadrilatères, des triangles et des polygones réguliers
À voir aussi
- Les formules de périmètre, d’aire et de volume
- Le périmètre et l’aire des triangles
- Le périmètre et l’aire des quadrilatères
- Le périmètre et l’aire des polygones réguliers
- Le périmètre et l’aire des figures décomposables
- La circonférence d'un cercle et l'aire d'un disque
- L’aire et le volume des solides