Metric Relations in a Circle

Metric relations in a circle are mathematical links between the various quantities in a circle.

In the same circle or in two congruent circles, two isometric chords are located the same distance from the centre and vice versa.

In the circle below:

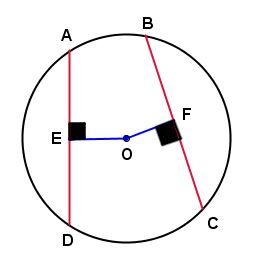
• If the measure of chord |\overline{AD}| is equal to the measure of chord |\overline{BC},| then the measure of line segment |\overline{EO}| is equal to the measure of line segment |\overline{FO}.|

• If the measure of line segment |\overline{EO}| is equal to the measure of line segment |\overline{FO},| then the measure of chord |\overline{AD}| is equal to the measure of chord |\overline{BC}.|

We can summarize as follows:

If |\mathrm{m}\overline{AD}=\mathrm{m}\overline{BC},| thus |\mathrm{m}\overline{EO}=\mathrm{m}\overline{FO};|
If |\mathrm{m}\overline{EO}=\mathrm{m}\overline{FO},| thus |\mathrm{m}\overline{AD}=\mathrm{m}\overline{BC}.|

Any diameter perpendicular to a chord bisects both the chord itself and each of the arcs it subtends.

In the circle below:

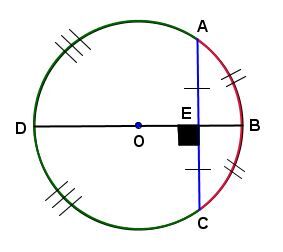
• If the measure of line segment |\overline{AE}| is equal to the measure of line segment |\overline{CE},| then the measure of arc |\overset{\huge\frown}{\small{AB}}| is equal to the measure of arc |\overset{\huge\frown}{\small{BC​}}| and the measure of arc |\overset{\huge\frown}{\small{AD}}| is equal to the measure of arc |\overset{\huge\frown}{\small{DC}};|

• If the measure of arc |\overset{\huge\frown}{\small{AB}}| is equal to the measure of arc |\overset{\huge\frown}{\small{BC}}| and the measure of arc |\overset{\huge\frown}{\small{AD}}| is equal to the measure of arc |\overset{\huge\frown}{\small{DC}},| then the measure of line segment |\overline{AE}| is equal to the measure of line segment |\overline{CE}.|

We can summarize as follows:

If |\mathrm{m}\overline{AE}=\mathrm{m}\overline{CE},| then |\mathrm{m}\overset{\huge\frown}{\small{AB}}=\mathrm{m}\overset{\huge\frown}{\small{BC}}| and |\mathrm{m}\overset{\huge\frown}{\small{AD}}=\mathrm{m}\overset{\huge\frown}{\small{DC}};|

if |\mathrm{m}\overset{\huge\frown}{\small{AB}}=\mathrm{m}\overset{\huge\frown}{\small{BC}}| and |\mathrm{m}\overset{\huge\frown}{\small{AD}}=\mathrm{m}\overset{\huge\frown}{\small{DC}},| then |\mathrm{m}\overline{AE}=\mathrm{m}\overline{CE}.|

Anything perpendicular to the end of a radius is tangent to the circle and vice versa.

In the circle below:

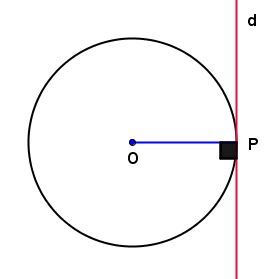
• If the line |d| goes through the endpoint |P| of radius |\overline{OP}| and is perpendicular to this radius, then line |d| is tangent to the circle with centre |O.|

• If the line |d| is tangent to the circle with centre |O,| then line |d| is perpendicular to the radius |\overline{OP}.|

We can summarize as follows:

If |d\perp\overline{OP},| then |d| is tangent to the circle;

if |d| is tangent to the circle, then |d\perp\overline{OP}.|

Two parallel lines, either secant or tangent, intersect two isometric arcs on that circle.

In the circle below:

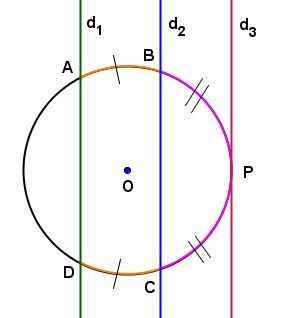
• If the secant lines |d_1| and |d_2| are parallel, then the measure of arc |\overset{\huge\frown}{\small{AB}}| is equal to the measure of arc |\overset{\huge\frown}{\small{DC}}.|

• If the secant lines |d_2| and |d_3| are parallel, then the measure of arc |\overset{\huge\frown}{\small{BP}}| is equal to the measure of arc |\overset{\huge\frown}{\small{CP}}.|

We can summarize as follows:

If |d_1\parallel d_2,| then |\mathrm{m}\overset{\huge\frown}{\small{AB}}=\mathrm{m}\overset{\huge\frown}{\small{DC}};|

if |d_2\parallel d_3,| then |\mathrm{m}\overset{\huge\frown}{\small{BP}}=\mathrm{m}\overset{\huge\frown}{\small{CP}}.|

A tangent to a circle is a straight line that intersects a circle at a single point.

An inscribed angle’s measure is half the measure of the arc located inside its sides.

In the circle below:

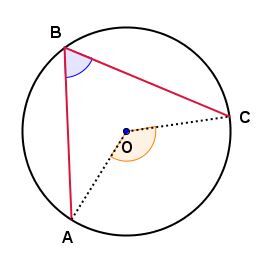
The measure of angle |ABC| is equal to half the measure of angle |AOC|.

We can summarize as follows:
||\begin{align} \mathrm{m}\angle ABC &= \frac{\mathrm{m}\overset{\huge\frown}{\small{AC}}}{2} \\
&= \frac{\mathrm{m}\angle{AOC}}{2}\end{align}||
For example,
||\begin{align}\mathrm{m}\angle AOC&=120^{\ \circ}\\
\mathrm{m}\angle ABC&=60^{\ \circ}\end{align}||

An angle with a vertex located between a circle and its centre measures half the sum of the measure of the two arcs formed by its extended sides.

In the circle below:

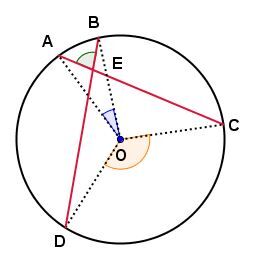
• The measure of angle | AEB| is equal to half of the sum of the measure of arcs |\overset{\huge\frown}{\small{AB}}| and |\overset{\huge\frown}{\small{CD}}.|

• The measure of angle |AEB| is equal to half of the sum of the measure of angles |AOB| and |COD.|

We can summarize as follows:

|\mathrm{m}\angle AEB=\dfrac{\mathrm{m}\overset{\huge\frown}{\small{AB}}+\mathrm{m}\overset{\huge\frown}{\small{CD}}}{2};|

|\mathrm{m}\angle AEB=\dfrac{\mathrm{m}\angle AOB+\mathrm{m}\angle COD}{2}.|

An angle with a vertex located outside a circle measures half of the difference between the measure of the arcs formed by its extended sides.

In the circle below:

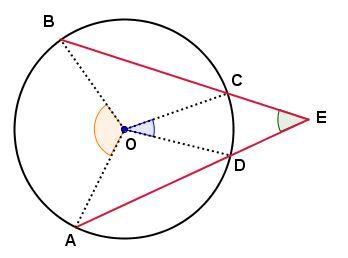
• The measure of angle |\angle AEB| is equal to half of the difference of the measure of arcs |\overset{\huge\frown}{\small{AB}}| and |\overset{\huge\frown}{\small{CD}}.|

• The measure of angle |\angle AEB| is equal to half of the difference of the measure of angles |\angle AOB| and |\angle COD.|

We can summarize as follows:

|\mathrm{m}\angle AEB=\dfrac{\mathrm{m}\overset{\huge\frown}{\small{AB}}-\mathrm{m}\overset{\huge\frown}{\small{CD​​}}}{2};|

|\mathrm{m}\angle AEB=\dfrac{\mathrm{m}\angle AOB-\mathrm{m}\angle COD}{2}.|

If, from a point |P| outside a circle of centre |O,| we run two tangents to points |A| and |B| on the circle, then line |OP| bisects angle |APB| and |\mathrm{m}\overline{PA}=\mathrm{m}\overline{PB}.|

In the circle below:

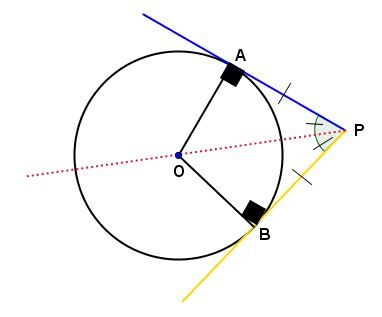
Since the half-lines |PA| and |PB| are tangent to the circle of centre |O,| angles |APO| and |BPO| are equal because |PO| bisects angle |APB| and the measure of |\overline{PA}| and |\overline{PB}| are equal.

We can summarize as follows.

|\mathrm{m}\overline{PA}=\mathrm{m}\overline{PB}| and
|\mathrm{m}\angle APO=\mathrm{m}\angle BPO=\dfrac{\mathrm{m}\angle APB}{2}.|

If, from a point |P| outside the centre circle |O,| we run two secants |PB| and |PD,| then the product of |\mathrm{m}\overline{PA}| and |\mathrm{m}\overline{PB}| is equal to the product of |\mathrm{m}\overline{PC}| and |\mathrm{m}\overline{PD}.|

In the circle below:

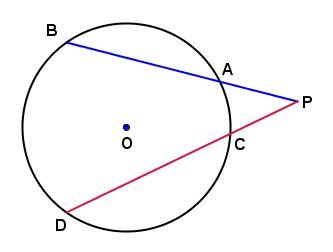
We can say:
||\mathrm{m}\overline{PA}\times\mathrm{m}\overline{PB}=\mathrm{m}\overline{PC}\times\mathrm{m}\overline{PD}||

Assuming the following measurements: ||\begin{align}\mathrm{m}\overline{PA}&=2.7\ \mathrm{cm}\\
\mathrm{m}\overline{PC}&=2.4\ \mathrm{cm}\\
\mathrm{m}\overline{CD}&=4.8\ \mathrm{cm}\end{align}||
We obtain:

||\begin{align}2.7\times\mathrm{m}\overline{PB}&=2.4\times(2.4+4.8)\\
&=6.4\ \mathrm{cm}\end{align}||
Therefore, the measure of |\overline{AB}| is  |6.4-2.7=3.7\ \mathrm{cm}.|

If, from a point |P| outside a circle of centre |O,| we lead a secant |PB| and a tangent |PC,| then the product of |\mathrm{m}\overline{PA}| and |\mathrm{m}\overline{PB}| is equal to the square of |\mathrm{m}\overline{PC}.|

In the circle below:

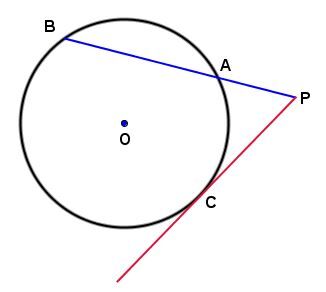
We can say:
||\mathrm{m}\overline{PA}\times\mathrm{m}\overline{PB}=(\mathrm{m}\overline{PC})^{2}||

Assuming the following measurements: ||\begin{align}\mathrm{m}\overline{PA}&=0.8\ \mathrm{cm}\\
\mathrm{m}\overline{AB}&=1.8\ \mathrm{cm}\end{align}||
We obtain:
||\begin{align}0.8\times(0.8+1.8)&=(\mathrm{m}\overline{PC})^{2}\\
\sqrt{2.08}&=\mathrm{m}\overline{PC}\\
1.44\ \mathrm{cm}&\approx\mathrm{m}\overline{PC}\end{align}||

When two chords intersect inside a circle, the product of the segments’ measure of one chord equals the product of the segments’ measure of the other.

In the circle below:

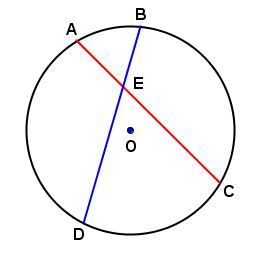
We can say:
||\mathrm{m}\overline{AE}\times\mathrm{m}\overline{CE}=\mathrm{m}\overline{BE}\times\mathrm{m}\overline{DE}||

Assuming the following measurements: ||\begin{align}\mathrm{m}\overline{AE}&=0.3\ \mathrm{cm}\\
\mathrm{m}\overline{CE}&=1.2\ \mathrm{cm}\\
\mathrm{m}\overline{DE}&=1.3\ \mathrm{cm}\end{align}||
We obtain:
||\begin{align}0.3\times1.2&=\mathrm{m}\overline{BE}\times1.3\\
0.28\ \mathrm{cm}&\approx\mathrm{m}\overline{BE}\end{align}||