Subjects
Grades
The Properties of the Step Function (Greatest Integer Function)
Concept sheet | Mathematics
Secondary
4-5
In the following animation, experiment with the parameters |a,| |b,| |h,| and |k| of the step function and observe the effects on the function. Afterwards, see the concept sheet to learn more about the function’s properties.
Properties of the Basic Step Function (Greatest Integer Function) |f(x)=[x]|
|
Property |
Characteristic of the Basic Form |
|---|---|
|
Equation |
|f(x)=[x]| |
|
Domain |
|\text{dom}f=\mathbb{R}| or depending on the context |
|
Range |
|\text{range}f=\mathbb{Z}| Only the integers |
|
|y|-intercept |
The graph of the basic step function crosses the |y|-axis at the origin, so the value of the |y|-intercept is |0|. |
|
|x|-intercept (zeroes of the function) |
The base function has zeroes over the following interval: |x \in [0,1[.| |
|
Variation: increasing and decreasing intervals |
The function is increasing over all |x|. It increases on |\mathbb{R}.| |
|
Vertex |
The graph does not have a vertex. |
|
Coordinates of a closed point of a step |
|(0,0)| |
|
Direction of points |
In the basic step function, each segment has a closed point on the left and an open point on the right. |
|
Extrema |
This function has no extrema. |
|
Positive and negative intervals |
The basic step function is positive for every |x \geq 0|. It is negative for every |x \leq 0|. |
|
Axis of symmetry |
The step function does not have an axis of symmetry |
|
Asymptotes |
There are no asymptotes. |
Properties of the Step Function (Greatest Integer Function) in Standard Form
|
Property |
Characteristic of the Standard Form |
|---|---|
|
Equation |
|f(x)=a[b(x-h)]+k| |
|
Coordinates of a closed point of a step |
|(h,k)| |
|
Domain |
|\text{dom} f =\mathbb{R}| or depending on the context |
|
Range |
|\text{range} f= \lbrace an + k\ \text{where } n \in \mathbb{Z}\rbrace| |
|
Variation: increasing and decreasing intervals |
If the parameters |a| and |b| have the same sign |(a b>0),| the function is increasing. If the parameters |a| and |b| have opposite signs |(ab<0),| the function is decreasing. |
|
Zeroes of the function |
If they exist, they are the values of |x| where |f (x)=0|. For them to exist, it is necessary that |k| is a multiple of |a.| |
|
|y|-intercept |
The value of |f (0).| |
|
Direction of points |
If |b| is positive, each step has a closed point on the left and an open point on the right. If |b| is negative, each step has an open point on the left and a closed point on the right. |
|
Positive and negative intervals |
Positive interval: interval of |x| where |f(x)\geq 0.| Negative interval: interval of |x| where |f(x)\leq 0.| |
|
Extrema |
None, unless the domain is restricted by the context. |
Determine the properties of the step function with the following equation. ||f(x)=-2\left[ \displaystyle \frac{1}{2}(x+1)\right]+2||
Drawing a graph of the function is recommended.
-
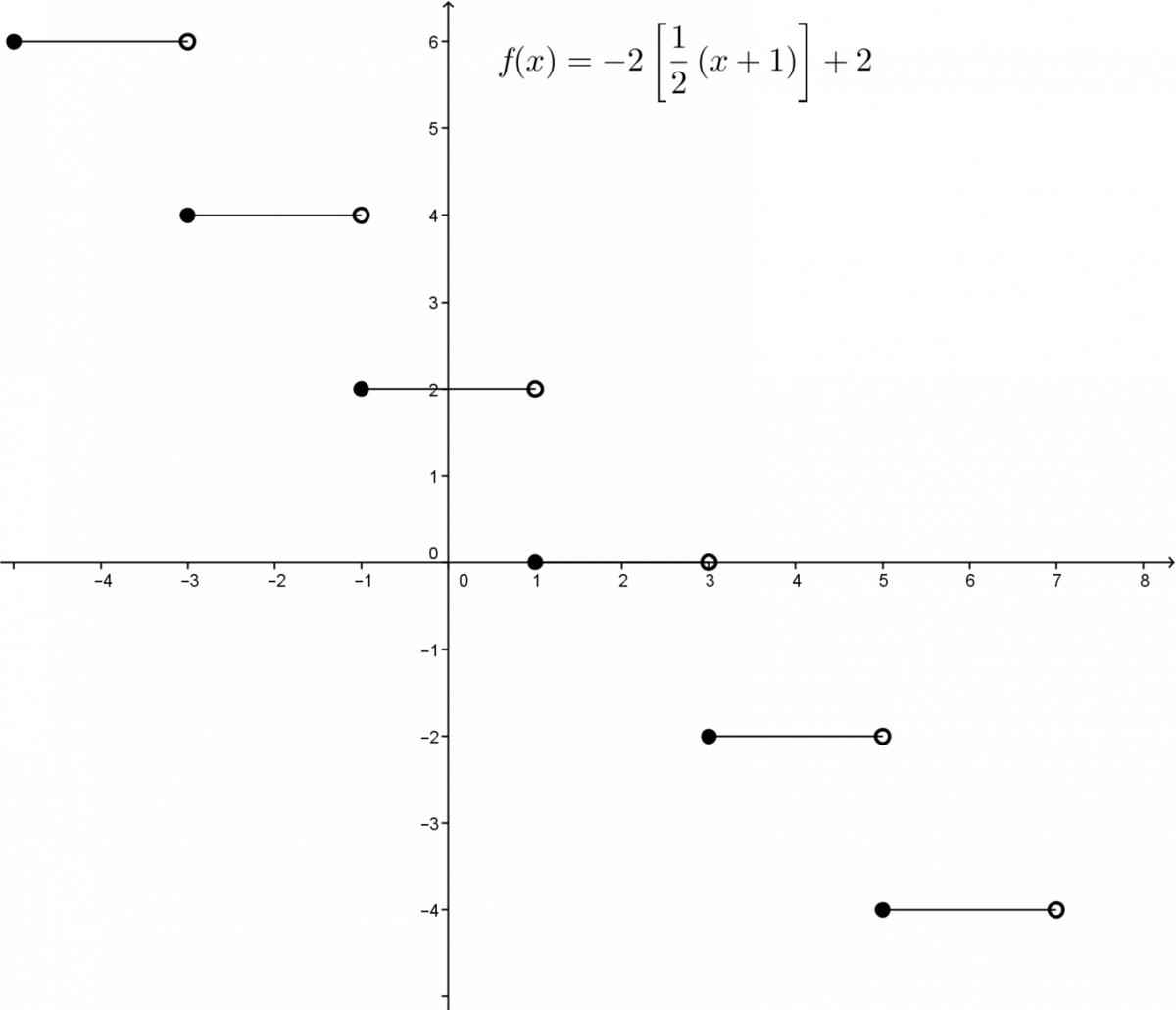
The coordinates of a closed end of a step are |(-1,2)=(h,k).|
-
The domain of the function is |\mathbb{R}.|
-
The range: since the parameter |k| has a value of |2| and the parameter |a| has a value of |-2,| the image of the function is: |\text{range } f= -2n + 2 \text{ where } n \in \mathbb{Z}|. The image of the function can also be expressed using curly brackets as |\lbrace ...,-4,-2,0,2,4,... \rbrace.|
-
The variation: the function is decreasing since the product |a \times b| is negative, given that |-2 \times \displaystyle \frac{1}{2} = -1.|
-
The function has zeroes since |2| is a multiple of |-2.| The zeroes can be determined either graphically or algebraically.
To calculate the zeroes, replace |f(x)| by |0| and then isolate the bracketed part. ||\begin{align}0 &= -2\left[ \displaystyle \frac{1}{2}(x+1) \right] + 2\\-2 &= -2\left[ \displaystyle \frac{1}{2}(x+1) \right]\\ 1 &= \left[ \displaystyle \frac{1}{2}(x+1) \right]\end{align}||Next, remember that if |[x]=a| for some |a \in \mathbb{Z},| then |a \leq x < a+1.|
Here, |a=1.| So, |1 \leq \displaystyle \frac{1}{2}(x+1) < 2|.
Now isolate |x|. ||\begin{align}1 &\leq \displaystyle \frac{1}{2}(x+1) < 2\\ 2 &\leq \phantom{\displaystyle \frac{1}{2}(}x+1\phantom{)}< 4\\1 &\leq \phantom{\displaystyle \frac{1}{2}(+} x \phantom{11)} < 3\end{align}||Therefore, the zeros of the function are the values of |x| in the interval |[1,3[.| -
The |y|-intercept of the function is calculated by replacing |x| with |0|. ||\begin{align}f(0) &= -2 \left[ \displaystyle \frac{1}{2}(0+1) \right] +2\\f(0) &= 2\end{align}|| Therefore, the |y|-intercept is |2.|
-
The direction of the points is full-empty (also defined as closed-open). This is because the parameter |b| is positive.
-
The positive and negative intervals:
-
The function is positive |(x \geq 0)| on the interval |]- \infty, 3[.|
-
It is strictly positive |(x>0)| on the interval |]-\infty, 1[.|
-
It is negative |(x \leq 0)| on the interval |[1, + \infty[.|
-
It is strictly negative |(x<0)| on the interval |[3,+\infty[.|
-
-
The function does not have any extrema.