Subjects
Grades
The Step Function (Greatest Integer Function)
Concept sheet | Mathematics
Secondary
4-5
Here is some basic information about the step function.
For additional information, consult the following concept sheets.
- The Role of the Parameters in a Step Function (Greatest Integer Function)
- Graphing a Step Function (Greatest Integer Function)
- Finding the Rule of a Step Function (Greatest Integer Function)
- The Properties of the Step Function (Greatest Integer Function)
- Solving a Greatest Integer Equation
- Solving Problems Involving the Step Function (Greatest Integer Function)
- The Inverse of the Step Function (Greatest Integer Function)
The Step Function
A function that is constant over intervals is called a step function. It is formed by platforms which are called steps. The vertical distance between the steps is informally called the step height.
A step function does not always have steps of the same length. The same is true for the step heights.
Here is an example graph of a step function.
The Step Function (Greatest Integer Function)
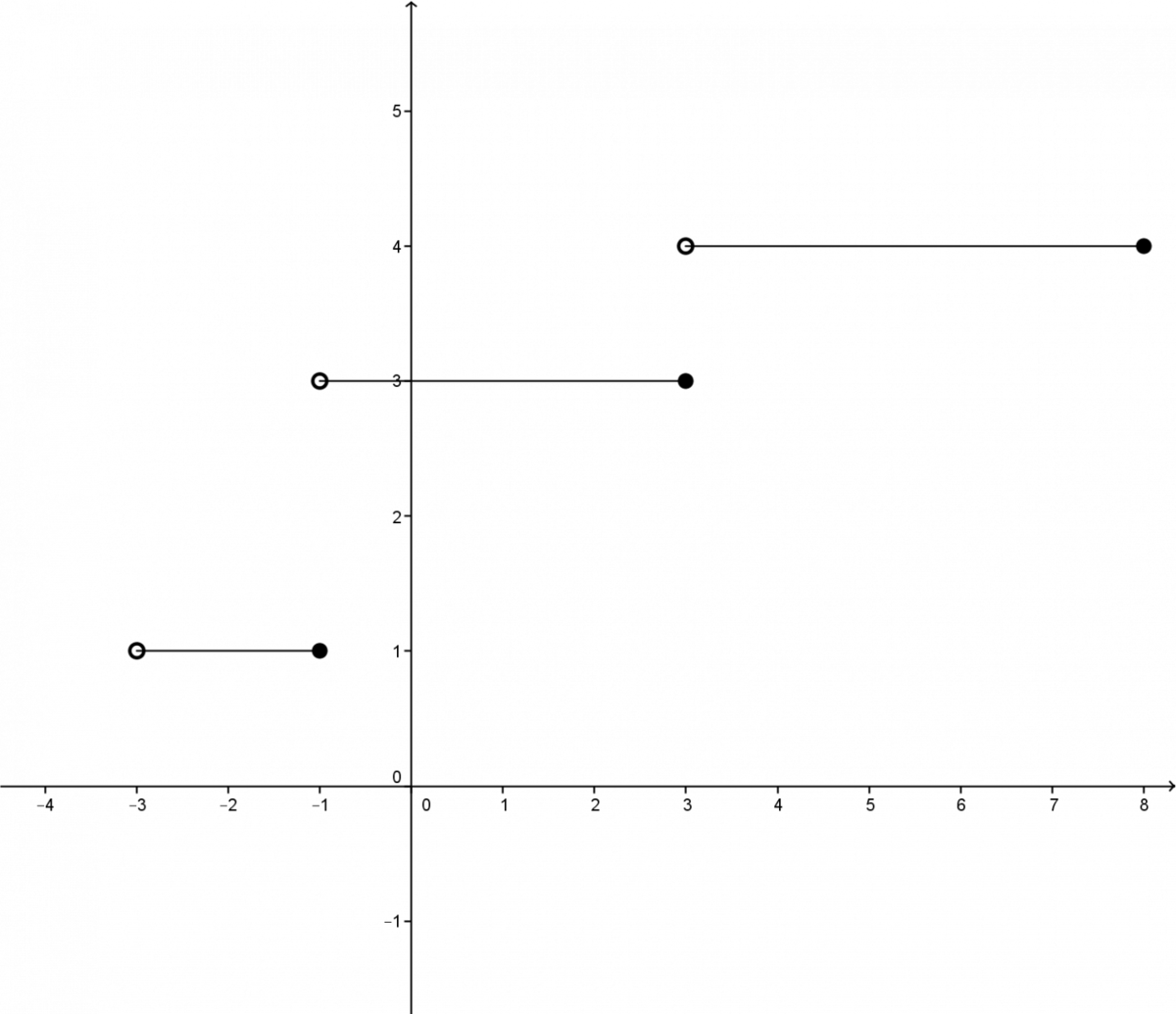
It is useful here to define the integer component of a number.
The integer part of a number, denoted |[x],| is the unique integer such that |[x] \leq x < [x] +1.| This quantity is also called the greatest integer less than or equal to |x.| The two names are synonymous.
Note: If |[x]=a|, where |a| is an integer, then |a \leq x < a+1.| Therefore, |x| belongs to the interval |[a,a+1[.|
|[2.3]=2,| we look for the largest integer less than or equal to |2.3.| Note that |2 \leq 2.3 < 3.|
|[-2.3]=-3,| we look for the largest integer less than or equal to |-2.3.| Note that |-3 \leq -2.3 < -2.|
|[45]=45,| we look for the largest integer less than or equal to |45.| Note that |45 \leq 45 < 46.|
The greatest integer function is a particular kind of step function.
A step function is a function |f|, such that for any real number |x|, |f(x)| is less than or equal to |x|.
The step function in its basic form has the following equation.
||f(x)=[x]||
In this function, the steps all have the same length and the step heights all have the same length as well |(1)|.
From now on, the term step function will refer to the greatest integer function specifically.
Here is the graph of the basic step function along with its table of values.
| |x| | |y| |
|---|---|
| |[-5,-4[| | |-5| |
| |[-4,-3[| | |-4| |
| |[-3,-2[| | |-3| |
| |[-2,-1[| | |-2| |
| |[-1,0[| | |-1| |
| |[0,1[| | |0| |
| |[1,2[| | |1| |
| |[2,3[| | |2| |
| |[3,4[| | |3| |
| |[4,5[| | |4| |
| |[5,6[| | |5| |
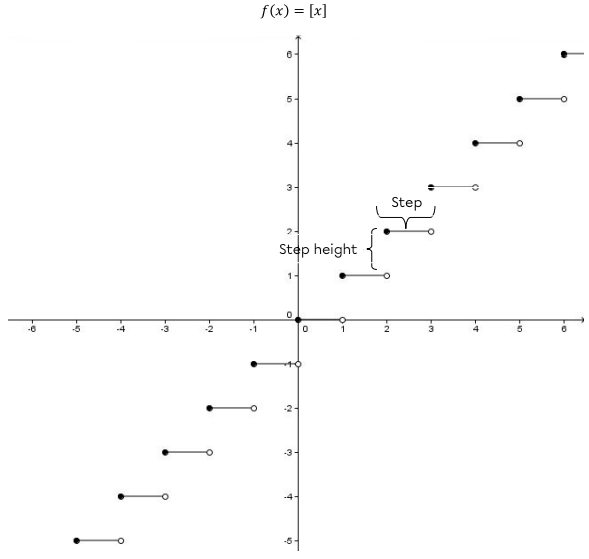
Open, or undefined, points are not part of the function. For instance, |[-1] \neq -2,| rather |[-1]=-1.| So it is normal that the point |(-1,-2)| is open and the point |(-1,-1)| is closed.
It is important to understand that, for a certain value of |f(x)|, the values of |x| correspond to an interval which has a closed end (defined point) and an open end (empty point). Each |x| in this interval maps to the same |f(x)|. This results in a platform, thus, the term step.