Subjects
Grades
Quadrilaterals
Concept sheet | Mathematics
Secondary
1-2
Quadrilaterals are closed polygons with 4 sides.
There are several classes of quadrilaterals. To classify them, analyze the measurements of the sides, the measurements of the angles, and the relative position of the sides.
The Classes of Quadrilaterals
Below is a diagram that illustrates the relationships between families of quadrilaterals.
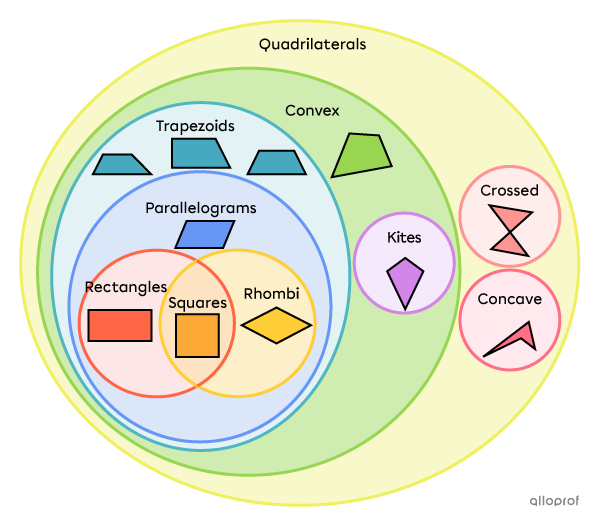
In the diagram we can distinguish between the 3 main classes of quadrilaterals: crossed, convex, and non-convex (or concave).
The convex quadrilaterals at the centre of the diagram have special characteristics.
A convex quadrilateral is a trapezoid if it has at least 1 pair of parallel sides.
A trapezoid with 2 pairs of parallel sides is a parallelogram.
A parallelogram with 4 congruent sides is a rhombus, while a parallelogram with 4 right angles is a rectangle.
Finally, a square is both a rectangle and a rhombus (with 4 congruent sides and 4 right angles).
Summary of the Properties
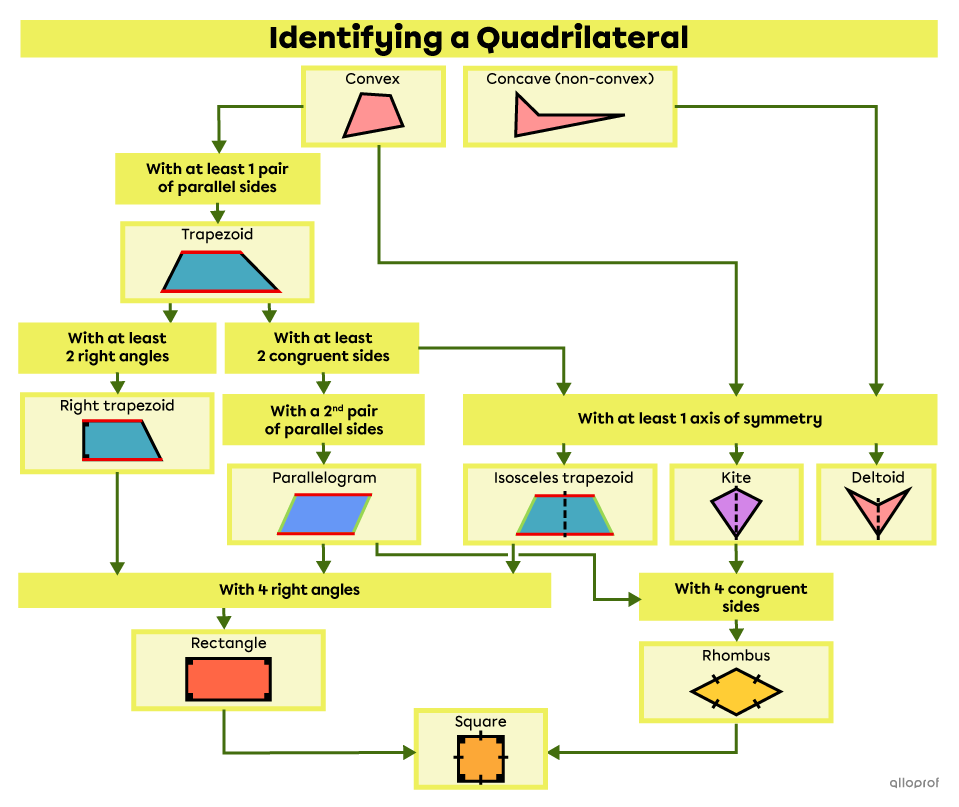
The image below is a decision tree that helps classify quadrilaterals based upon their properties.
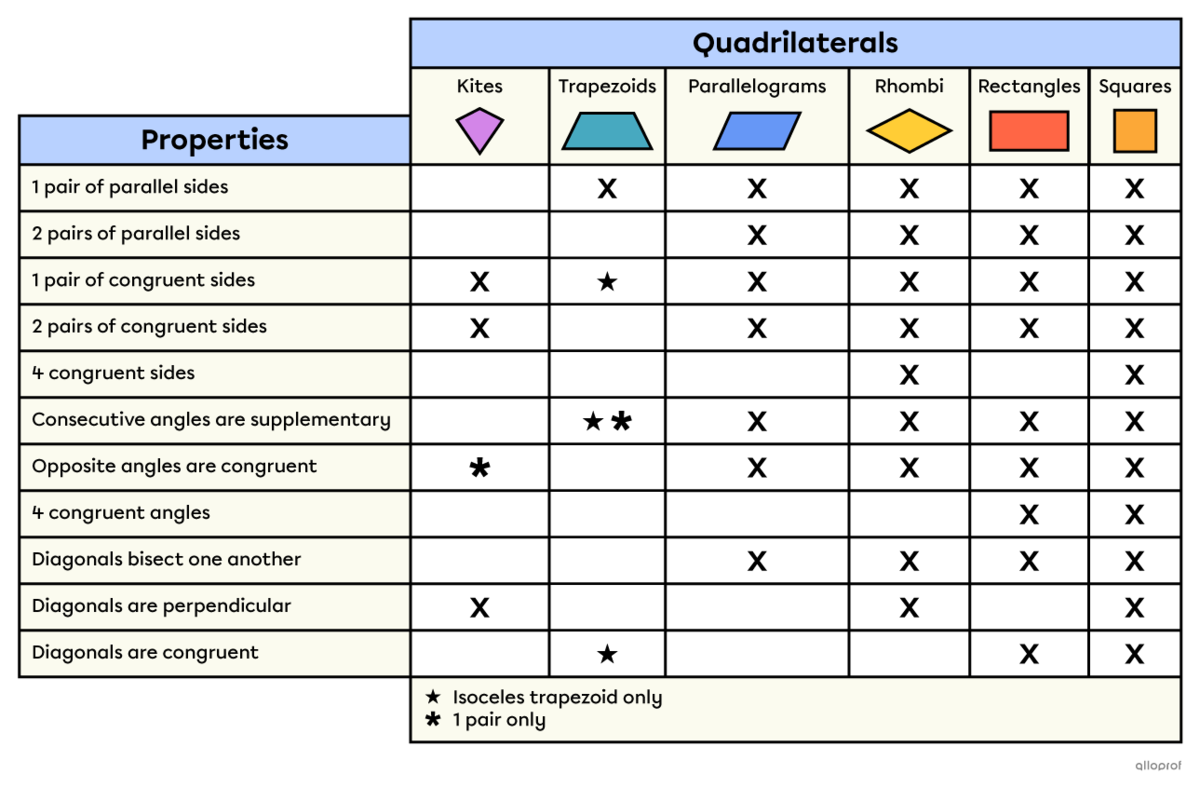
Below is a table that summarizes the various properties of quadrilaterals.
The Kite
A kite is a convex quadrilateral with 2 pairs of adjacent congruent sides.
The kite has the following properties:
-
1 pair of opposite, congruent angles
-
diagonals that are perpendicular.
Definition
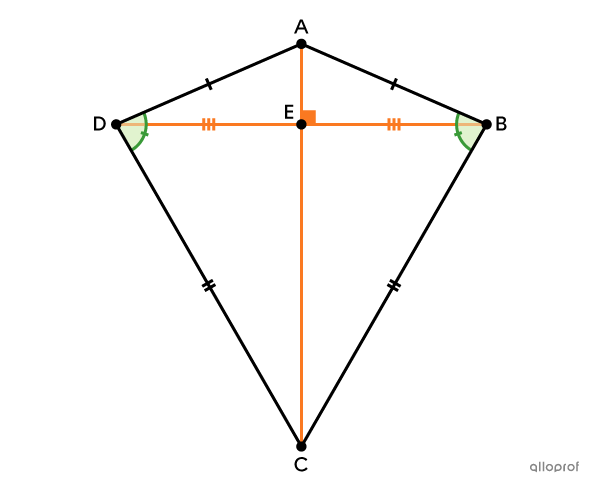
It has 2 pairs of adjacent congruent sides.||\begin{align}\overline{AB} &\cong \overline{AD}\\\overline{BC} &\cong \overline{CD}\end{align}||
Properties
It has 1 pair of opposite, congruent angles.||\angle{ABC}\cong\angle{ADC}||
Its diagonals are perpendicular.||\overline{AC}\perp\overline{BD}||
The Trapezoid
A trapezoid is a convex quadrilateral with at least 1 pair of parallel sides.
Definition
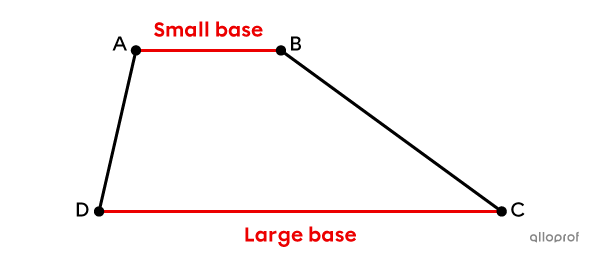
It has at least 1 pair of parallel sides.||\overline{AB} \parallel \overline{CD}||
The Right Trapezoid
A right trapezoid is a trapezoid with at least 2 right angles.
Definition
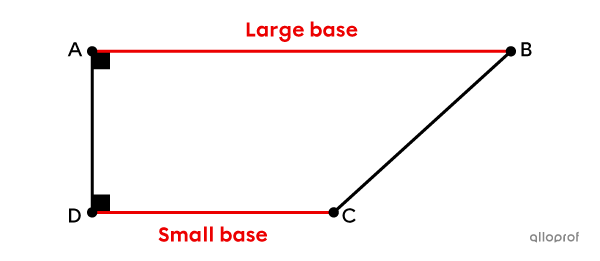
It has at least 1 pair of parallel sides.||\overline{AB} \parallel \overline{CD}||
It has 2 right angles.||\begin{align}\text{m}\angle{DAB}&=90^\circ\\ \text{m}\angle{ADC}&=90^\circ\end{align}||
The Isosceles Trapezoid
An isosceles trapezoid is a trapezoid with non-parallel sides that are congruent.
The isosceles trapezoid has the following properties:
-
2 pairs of adjacent supplementary angles
-
2 pairs of adjacent congruent angles
-
diagonals that are congruent.
Definition
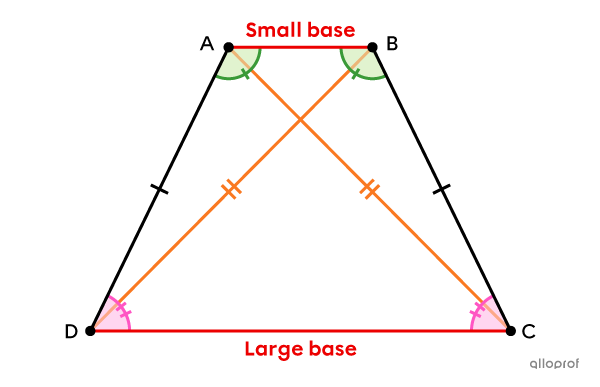
It has at least 1 pair of parallel sides.||\overline{AB} \parallel \overline{CD}||
Its non-parallel sides are congruent.||\overline{AD}\ \cong\ \overline{BC}||
Properties
It has 2 pairs of adjacent supplementary angles.||\begin{align}\text{m}\angle{BAD}+\text{m}\angle{ADC}&=180^\circ\\ \text{m}\angle{ABC}+\text{m}\angle{BCD}&=180^\circ\end{align}||
It has 2 pairs of adjacent congruent angles.||\begin{align}\angle{BAD}&\cong\angle{ABC}\\ \angle{ADC}&\cong\angle{BCD}\end{align}||
Its diagonals are congruent.||\overline{AC}\cong\overline{BD}||
The Parallelogram
A parallelogram is a convex quadrilateral with 2 pairs of opposite sides that are parallel.
The parallelogram has the following properties:
-
opposite angles that are congruent
-
2 pairs of adjacent supplementary angles
-
opposite sides that are congruent
-
diagonals that bisect each other.
Definition
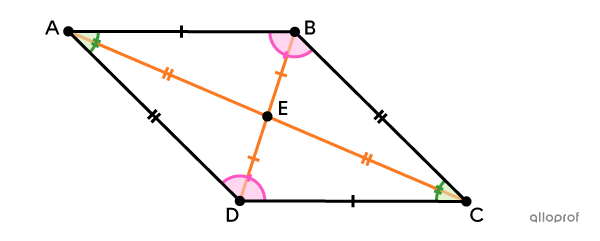
It has 2 pairs of opposite sides that are parallel.||\begin{align}\overline{AB} &\parallel \overline{CD}\\\overline{AD} &\parallel \overline{BC}\end{align}||
Properties
Its opposite angles are congruent.||\begin{align}\angle{ABC}&\cong\angle{ADC}\\ \angle{DAB}&\cong\angle{BCD}\end{align}||
It has 2 pairs of adjacent supplementary angles.||\begin{align}\text{m}\angle{BAD}+\text{m}\angle{ADC}&=180^\circ\\\text{m}\angle{BAD}+\text{m}\angle{ABC}&=180^\circ\\ \text{m}\angle{ABC}+\text{m}\angle{BCD}&=180^\circ\\\text{m}\angle{ADC}+\text{m}\angle{BCD}&=180^\circ\end{align}||
Its opposite sides are congruent.||\begin{align}\overline{AB} &\cong \overline{CD}\\\overline{AD} &\cong \overline{BC}\end{align}||
Its diagonals bisect one another.||\begin{align}\overline{BE}&\cong \overline{DE}\\ \overline{AE}&\cong \overline{CE}\end{align}||
The Rhombus
A rhombus is a convex quadrilateral with 4 congruent sides.
The rhombus has the following properties:
-
opposite angles that are congruent
-
adjacent angles that are supplementary
-
opposite sides that are parallel
-
diagonals that bisect one another and are perpendicular.
Definition
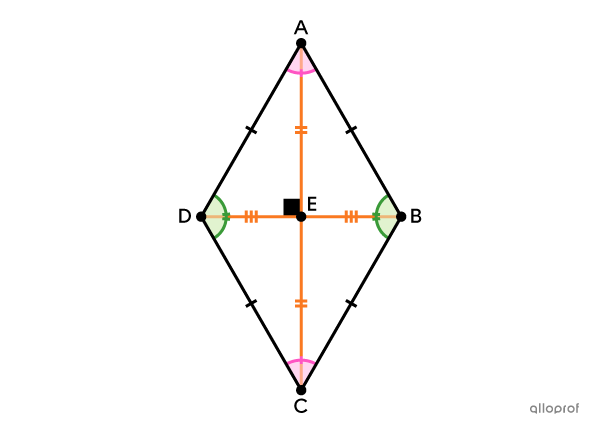
It has 4 congruent sides.||\overline{AB}\cong \overline{BC}\cong \overline{CD}\cong \overline{AD}||
Properties
Its opposite angles are congruent.||\begin{align}\angle{ABC}&\cong\angle{ADC}\\ \angle{DAB}&\cong\angle{DCB}\end{align}||
Its adjacent angles are supplementary.||\begin{align}\text{m}\angle{DAB}+\text{m}\angle{ABC}&=180^\circ\\
\text{m}\angle{ABC}+\text{m}\angle{BCD}&=180^\circ\\
\text{m}\angle{BCD}+\text{m}\angle{CDA}&=180^\circ\\
\text{m}\angle{CDA}+\text{m}\angle{DAB}&=180^\circ\end{align}||
Its opposite sides are parallel.||\begin{align}\overline{AB} &\parallel \overline{CD}\\\overline{AD} &\parallel\overline{BC}\end{align}||
Its diagonals bisect one another.||\begin{align}\overline{DE}&\cong \overline{BE}\\ \overline{AE}&\cong \overline{CE}\end{align}||
Its diagonals are perpendicular.||\overline{AC}\perp\overline{BD}||
The Rectangle
A rectangle is a convex quadrilateral with 4 right angles.
Definition
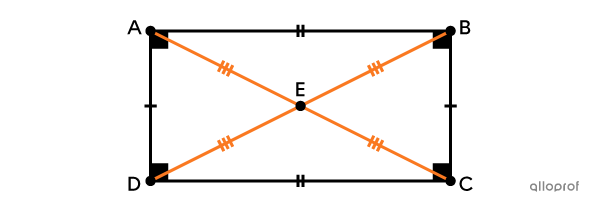
It has 4 angles that measure |90^\circ.|||\text{m}\angle{ABC}=\text{m}\angle{BCD}=\text{m}\angle{CDA}=\text{m}\angle{DAB}=90^\circ||
Properties
It has 2 pairs of opposite sides that are parallel.||\begin{align}\overline{AB} &\parallel \overline{CD}\\\overline{AD} &\parallel \overline{BC}\end{align}||
It has 2 pairs of opposite sides that are congruent.||\begin{align}\overline{AB} &\cong \overline{CD}\\\overline{AD} &\cong \overline{BC}\end{align}||
Its diagonals are congruent.||\overline{AC}\cong\overline{DB}||
Its diagonals bisect each other.||\begin{align}\overline{AE}&\cong \overline{CE}\\ \overline{DE}&\cong \overline{BE}\end{align}||
The Square
A square is a quadrilateral with 4 right angles and 4 congruent sides.
The rectangle has the following properties:
-
opposite sides that are parallel
-
diagonals that are perpendicular, bisect each other, and are congruent.
Definition
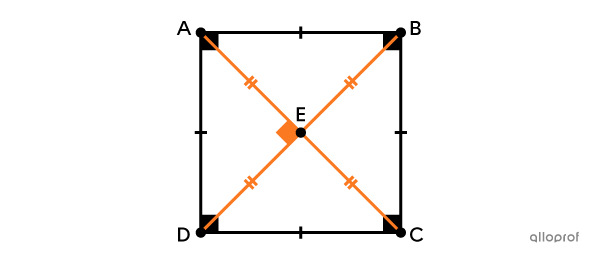
It has 4 right angles.||\text{m}\angle{ABC}=\text{m}\angle{BCD}=\text{m}\angle{CDA}=\text{m}\angle{DAB}=90^\circ||
It has 4 congruent sides.||\overline{AB} \cong \overline{BC}\cong \overline{CD} \cong \overline{AD}||
Properties
It has 2 pairs of parallel sides. ||\begin{align}\overline{AB} &\parallel \overline{CD}\\\overline{AD} &\parallel \overline{BC}\end{align}||
Its diagonals are perpendicular.||\overline{AC}\perp\overline{BD}||
Its diagonals bisect each other.||\begin{align}\overline{AE}&\cong \overline{CE}\\ \overline{BE}&\cong \overline{DE}\end{align}||
Its diagonals are congruent.||\overline{AC}\cong\overline{BD}||