The Composition of Geometric Transformations in a Cartesian Plane

When several geometric transformations are completed successively, the rule that connects these transformations is a composition and the result is called the composite. We use the symbol |\circ| that is read as "composite".

The transformations of a composition are always completed from right to left.

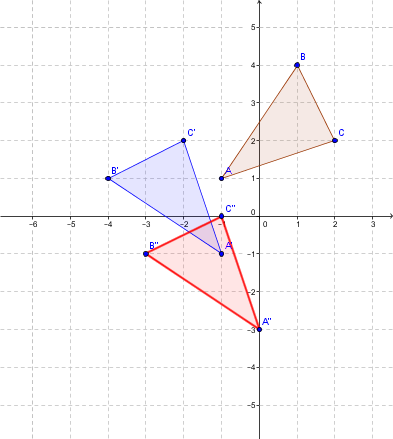
Consider the triangle |ABC|. We want to complete the transformation |t_{(1,-2)} \circ r_{(O,90°)}.|

At the start, complete a centre rotation |O| (here, it is the origin of the Cartesian plane) followed by a translation.

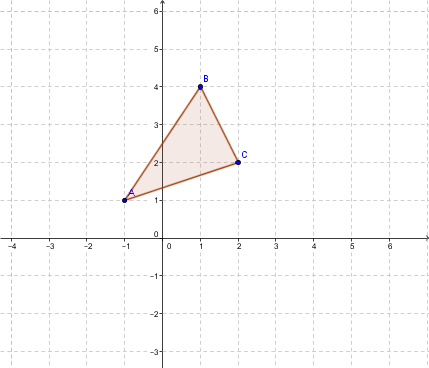
The coordinates of the vertices of the triangle |ABC| are: 

• |A(-1,1)|; 

• |B(1,4)|; 

• |C(2,2)|.

 
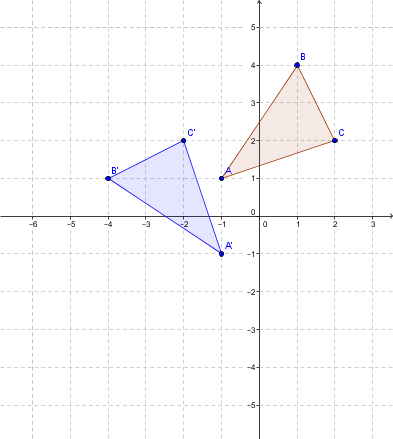
Step 1: Complete the rotation with centre |O| and angle |90°|  in a counterclockwise direction

Use the following rule |r_{(O,90°)}:(x,y) \mapsto (-y,x)|. 

|A=(-1,1) \mapsto (-1,-1)=A'|; 
|B=(1,4) \mapsto (-4,1)=B'|; 
|C=(2,2 \mapsto (-2,2)=C'|.

The blue triangle is obtained.

Step 2: Complete the translation with the rule |t_{(1,-2)}:(x,y) \mapsto (x+1,y-2)|

After completing it, the following points are obtained. 

• |A'=(-1,-1) \mapsto (0,-3)=A''|; 

• |B'=(-4,1) \mapsto (-3,-1)=B''|; 

• |C'=(-2,2) \mapsto (-1,0)=C''|.

This gives the red triangle which is the image figure.