Subjects
Grades
The Composition of Transformations
Concept sheet | Mathematics
Secondary
1-2
Once each of the geometric transformations have been mastered, they can be used with the same initial figure. In this case, it becomes a composition of transformations.
A composition of transformations is a sequence of transformations.
In terms of notation, for example, |t \circ s| is written "|t| composite |s|" and it means we must perform the reflection first and the translation second. In short, geometric transformations must be carried out from right to left.
Constructing a Composition of Transformations
It is important to follow the composition order presented to acquire the desired image figure.
According to the following drawing:
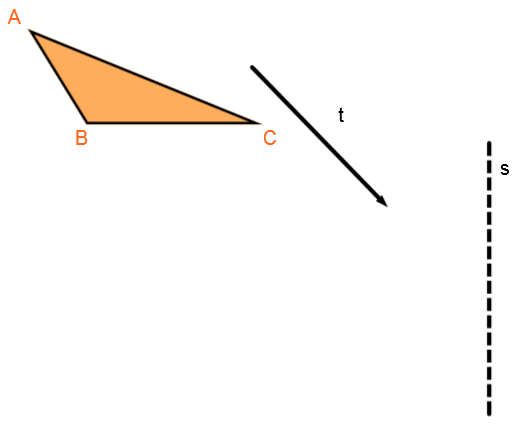
Perform the composition of transformations |s\circ t|
-
Identify the transformation order
Perform the translation |t| and apply a reflection across the axis |s|. -
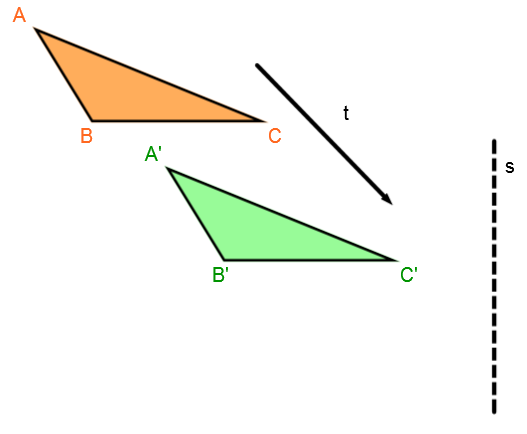
Perform the first transformation
Perform the translation |t| on the initial figure.
-
Perform the second transformation
Perform the reflection on the transformation image and not on the initial figure.
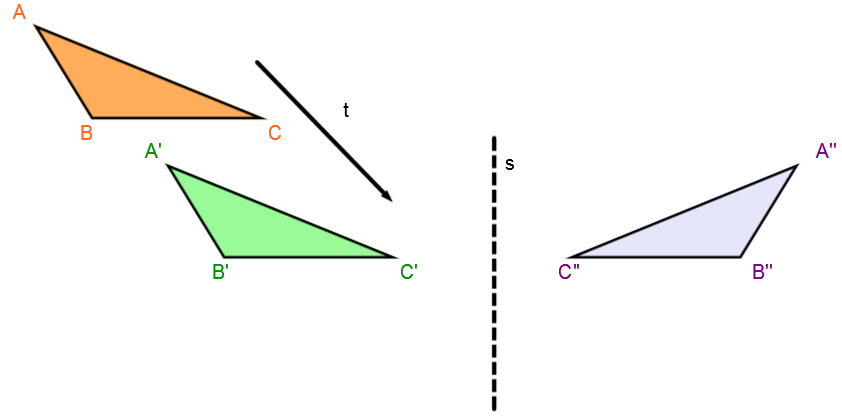
Among all the possible combinations, one has a particular name.
When a composition is made up of a translation and a reflection, and the translation arrow is parallel to the axis of reflection, the composition is called a glide reflection.
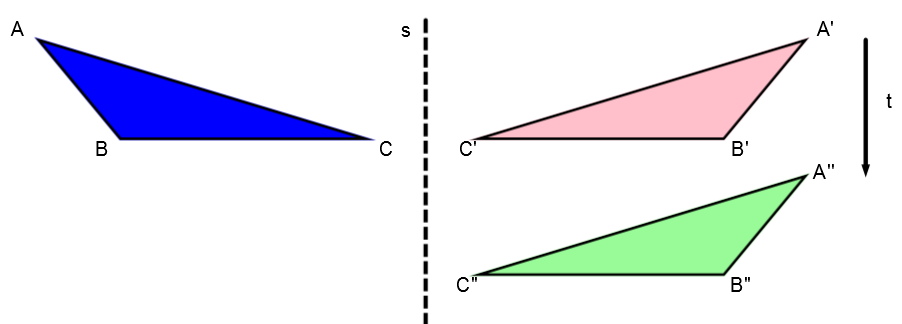
In this example, the axis of symmetry |s| is parallel to the translation arrow |t|.
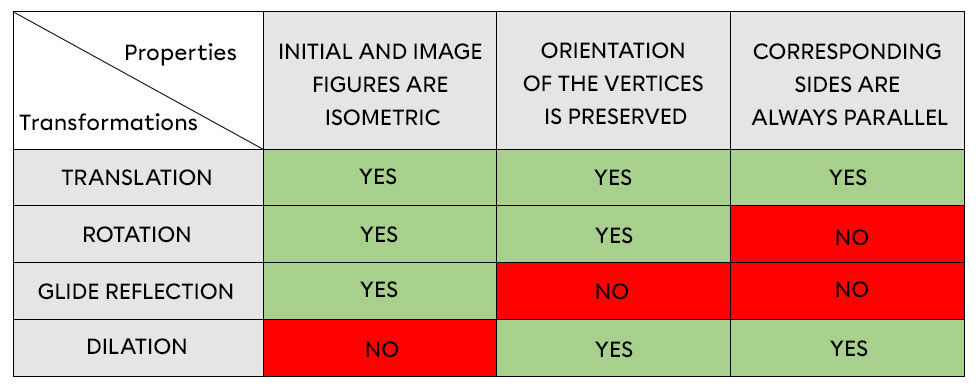
To distinguish between the four basic geometric transformations, observe their properties.
Summary of the Properties of Geometric Transformations
