Subjects
Grades
Properties of the Absolute Value Function
Concept sheet | Mathematics
Secondary
5
Table of contents
In the following interactive animation, experiment with the parameters |a,| |h,| and |k| of the absolute value function and observe how they affect the properties of the function. Afterwards, read the concept sheet to learn more about the function’s properties.
| PROPERTIES | ABSOLUTE VALUE FUNCTION IN STANDARD FORM ||f(x)=\color{red}{a}\mid x-\color{blue}{h} \mid + \color{green}{k}|| |
|---|---|
| Domain | |x \in \mathbb{R}| |
| Range | If |a>0,| then |[k, \infty[.| If |a<0,| then |]-\infty,k].| |
| |\boldsymbol{y}|-intercept | Replace |x| with |0| in the equation and calculate the value of |y.| This value will be the |y|-intercept. |
| |\boldsymbol{x}|-intercept (zeroes of the function) | If |a| and |k| have different signs, then there will be two distinct zeroes. If |k=0,| there will be a single zero. If |a| and |k| have the same sign, there will be no zero. |
| Vertex | |(h,k)| |
| Variation or increasing and decreasing intervals | If |a>0,| then the function decreases over the interval |]-\infty,h]| and increases over the interval |[h,\infty[.| If |a<0,| then the function increases over the interval |]-\infty,h]| and decreases over the interval |[h,\infty[.| |
| Extrema | |k| This is a maximum if |a<0| and a minimum if |a>0.| |
| Sign or positive and negative intervals | If |a>0| and |k>0,| there are no |x|-intercepts and the function is positive for all |x.| If |a<0| and |k<0,| there are no |x|-intercepts and the function is negative for all |x.| If |a>0| and |k=0,| there is only one |x|-intercept |(h,0)| and the function is positive for all |x.| If |a<0| and |k=0,| there is only one |x|-intercept |(h,0)| and the function is negative for all |x.| If |a>0| and |k<0,| there are two |x|-intercepts and the function is negative for the interval of |x| between the two |x|-intercepts and positive for all other |x.| If |a<0| and |k>0,| there are two |x|-intercepts and the function is positive for the interval of |x| between the two |x|-intercepts and negative for all other |x.| |
| Axis of symmetry | The absolute value function has an axis of symmetry. |x=h| |
| Asymptotes | The absolute value function has no asymptotes. |
Determine the properties of the absolute value function |f(x) = \displaystyle - \frac{1}{2} \mid x+1 \mid +2.|
It is useful to sketch a graph of the function.
The vertex is |(-1,\ 2)| and the function opens downwards since |a<0.|
-
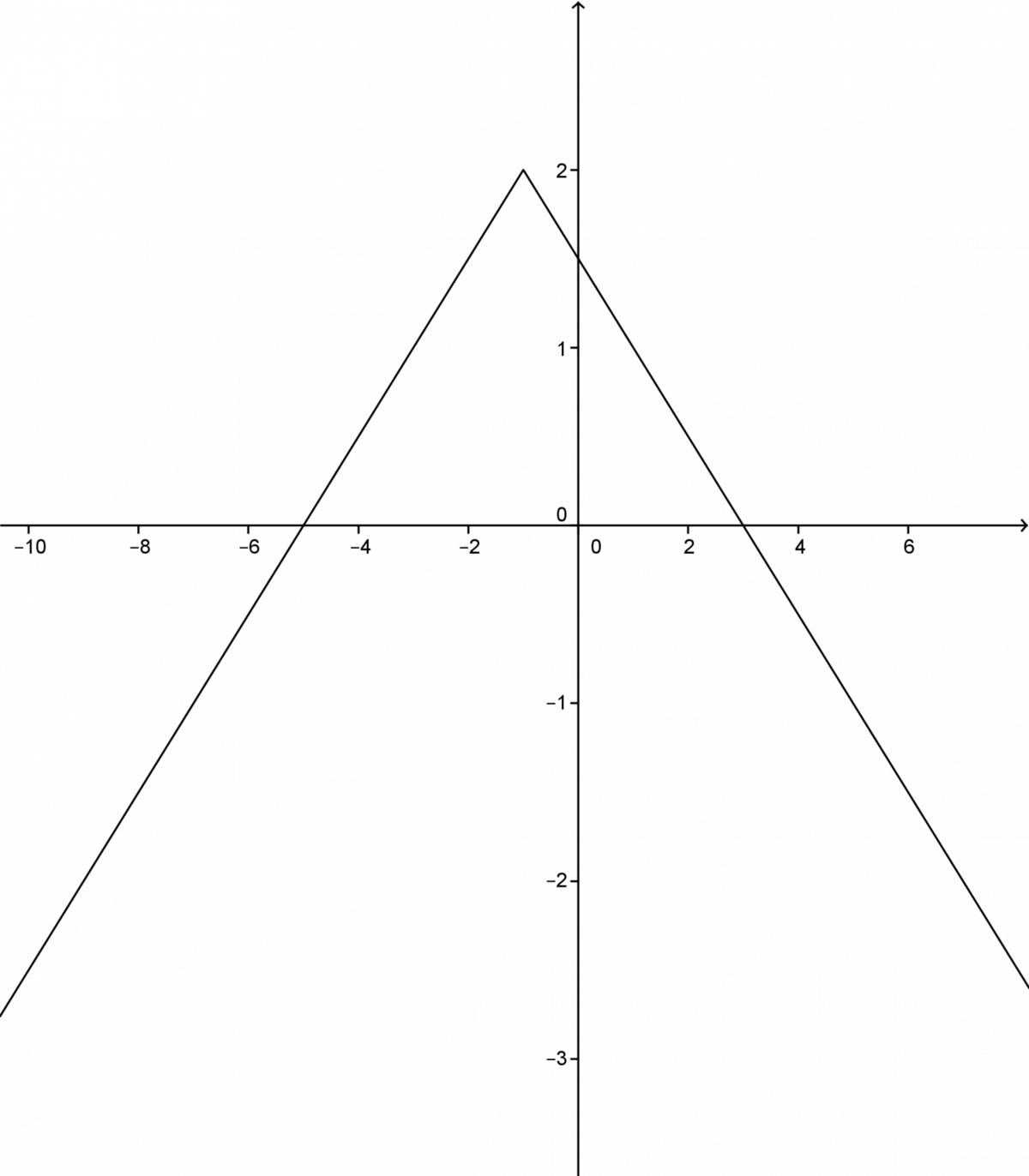
The domain of the function is the set of real numbers denoted as | \mathbb{R}.|
-
The range of the function corresponds to the interval |(- \infty, 2].|
-
To calculate the |y|-intercept, simply replace |x| with |0.| ||\begin{align}f(0) &= \displaystyle - \frac{1}{2} \mid 0 + 1 \mid +2\\ f(0) &= \displaystyle \frac{3}{2}\end{align}||
Therefore, the y|-intercept is | \displaystyle \frac{3}{2}.|
-
To calculate the zeroes of the function, just replace |f(x)| with |0| and isolate |x.| ||\begin{align} 0 &= \displaystyle - \frac{1}{2} \mid x+1 \mid +2\\ -2 &= \displaystyle - \frac{1}{2} \mid x +1 \mid\\ 4 &= \mid x +1 \mid \end{align}||
Here, use the definition of the absolute value. ||\begin{align}4 &=x+1 &-4 &= x+1 \\ 3 &=x &-5 &= x\end{align}||
Therefore, the two zeroes are |-5| and |3.|
-
Variation: the function is increasing over |(- \infty, -1]| and decreasing over |[-1, + \infty).|
-
Extrema: |a| is negative, thus, the function has a maximum of 2.
-
Sign — Positive and Negative Intervals: using the direction the function opens and the zeroes found, the positive and negative intervals of of the function are the following:
-
it will be positive over |[-5,3];|
-
it will be negative over |(-\infty,-5] \cup [3, +\infty).|
-
-
The equation for the axis of symmetry is |x=-1.|