Subjects
Grades
The Role of the Parameters in an Absolute Value Function
Concept sheet | Mathematics
Secondary
5
Table of contents
- Top of page
- Animation for Manipulating Parameters
- Analyzing Parameter |a|
- A Vertical Scaling of the Curve by a Factor of |a|
- A Reflection of the Function’s Graph Across the |x|-Axis
- Analyzing Parameter |b|
- A Horizontal Scaling of the Curve by |\dfrac{1}{b}|
- Analyzing Parameter |h|
- A Horizontal Translation of the Whole Function
- Analyzing Parameter |k|
- A Vertical Translation of the Whole Function
- See Also
Adding the parameters |a,| |b,| |h,| and |k| to the basic function |f(x)={\mid}x{\mid}| results in the standard form (or transformed form) of the absolute value function.
The standard form of the absolute value function is: ||f(x)=a {\mid}b(x-h){\mid} +\ k|| where |a,| |b,| |h,| and |k| are real numbers that act as parameters.
Note: The parameters |a| and |b| are always non-zero.
The point |(h,k)| corresponds to the vertex of the function.
With a few manipulations, we obtain an equation with three parameters |(a, h, k)| by applying the following property:
|{\mid}x \times y{\mid} = {\mid}x{\mid} \times {\mid}y{\mid}.|
|f(x) = a {\mid}b(x-h){\mid} + k|
|f(x)= a {\mid}b{\mid} {\mid}x - h{\mid} + k|
|f(x) = \mathbb{a} {\mid}x - h{\mid} + k| where |\mathbb{a} = a {\mid}b{\mid}|
Be careful! In the last equation, |\mathbb{a}| corresponds to the product of parameters |a| and |b.| Therefore, its effect is the equivalent of the combined effect of the two parameters.
Animation for Manipulating Parameters
Experiment with the parameters |\mathbb{a}|, |h,| and |k| in the interactive animation to see how they affect the absolute value function. Observe the changes that take place on the transformed curve (in black) compared to the base function (in blue). Use this opportunity to observe the effect of modifying the parameters on the properties of the function. Afterwards, read the concept sheet to learn more about each of the parameters.
Note: Simply use the equation |f(x)=\mathbb{a} {\mid}x - h{\mid} + k| since the parameter |b| is superfluous.
Analyzing Parameter |a|
A Vertical Scaling of the Curve by a Factor of |a|
When |{\mid}a{\mid} > 1 |
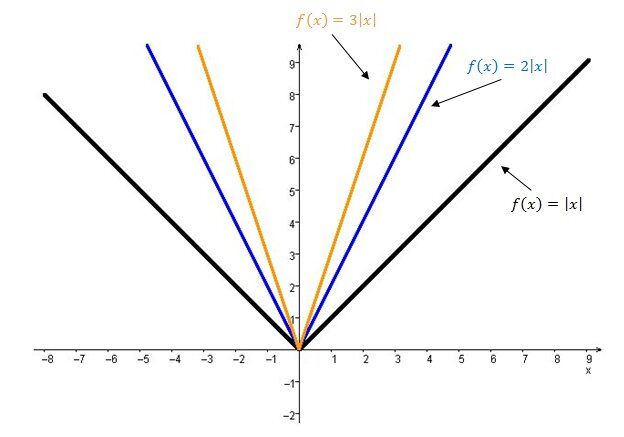
The larger the absolute value of the parameter |a|, the closer the two branches of the graph of the absolute value function are to the |y|-axis since the curve stretches vertically. It looks like the graph’s opening narrows.
When |0< {\mid}a{\mid} < 1 |
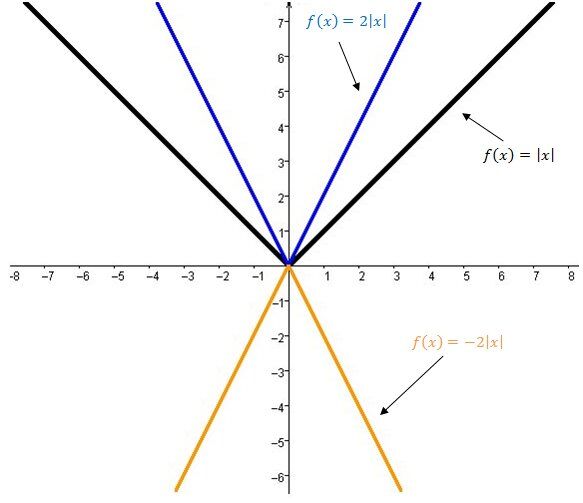
The smaller (closer to |0|) the parameter |a|, the more the two branches of the graph of the absolute value function collapse toward the |x|-axis. It looks like the graph’s opening becomes wider.
A Reflection of the Function’s Graph Across the |x|-Axis
The parameter |a| is also responsible for the orientation of the graph of the absolute value function.
When |a| is positive |(a>0) |
The absolute value function’s graph opens upwards.
When |a| is negative |(a<0) |
The absolute value function’s graph opens downwards.
Analyzing Parameter |b|
A Horizontal Scaling of the Curve by |\dfrac{1}{b}|
When |{\mid}b{\mid} > 1|
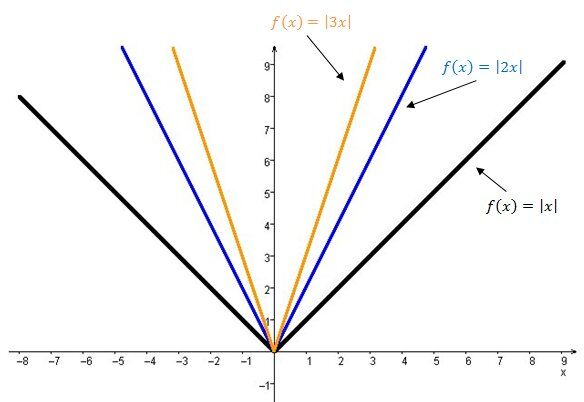
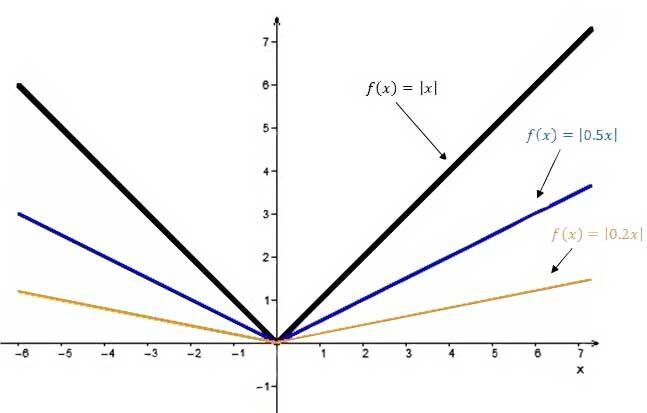
The larger the absolute value of the parameter |b|, the narrower the opening of the graph of the absolute value function.
When |0< {\mid}b{\mid} < 1|
The smaller (nearer |0|) the parameter |b|, the wider the opening of the graph of the absolute value function.
Analyzing Parameter |h|
A Horizontal Translation of the Whole Function
When |h| is positive |(h>0) |
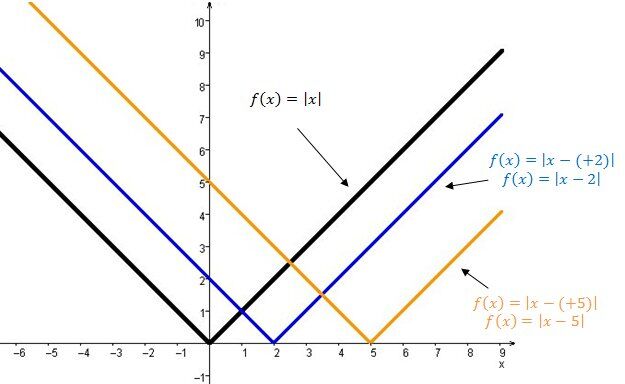
The graph of the absolute value function moves to the right.
When |h| is negative |(h<0) |
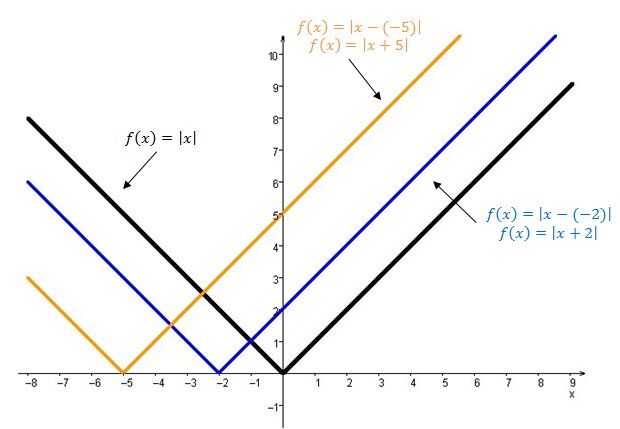
The graph of the absolute value function moves to the left.
Analyzing Parameter |k|
A Vertical Translation of the Whole Function
When |k| is positive |(k>0)|
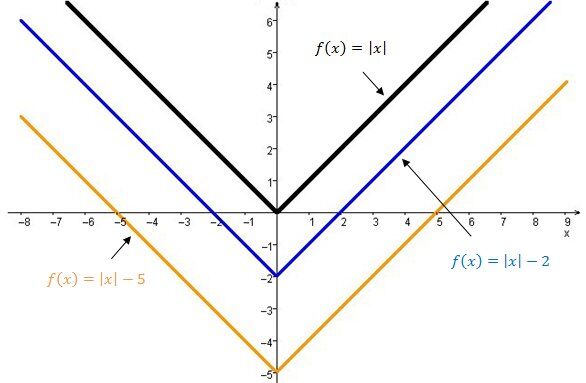
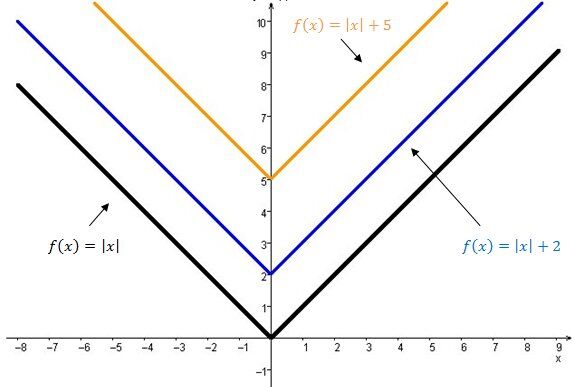
The graph of the absolute value function moves upwards.
When |k| is negative |(k<0)|
The graph of the absolute value function moves downwards.
