Matières
Niveaux
La démonstration en géométrie analytique
Fiche | Mathématiques
Secondaire
4-5
En mathématique, une démonstration est définie comme une suite d'affirmations mathématiques logiquement liées permettant de prouver un raisonnement ou un résultat.
Tout comme en géométrie classique, des démonstrations sont utilisées en géométrie analytique afin de démontrer la véracité d'une affirmation donnée. Les points suivants sont à retenir.
- Pour effectuer une bonne démonstration en géométrie analytique, il faut effectuer une représentation graphique, dans un plan cartésien, de la proposition sur laquelle on travaille.
- Il est très important de limiter le plus possible le nombre de variables utilisées pour annoter les points importants sur notre figure. Il est conseillé de se tenir près des axes.
- Il faut bien identifier l'hypothèse, qui correspond à toutes les informations qui sont dans la proposition et qui sont vraies sans démonstration. On peut les utiliser pour la démonstration.
- Il faut relever clairement la conclusion, qui correspond à ce que l'on voudra démontrer.
- N'hésitez pas à chercher les mots que vous jugez compliqués.
- Plusieurs outils de géométrie analytique pourront être utiles. Avant même de commencer la rédaction de votre démonstration, ayez en tête les outils que vous utiliserez.
- N'hésitez pas à vous faire un brouillon de votre démonstration.
- Faites votre démonstration le plus clairement possible afin qu'une autre personne puisse la lire et la valider.
Voici un exemple de démonstration en géométrie analytique.
Démontrez que, dans un triangle rectangle, le point milieu de l'hypoténuse est équidistant des trois sommets du triangle.
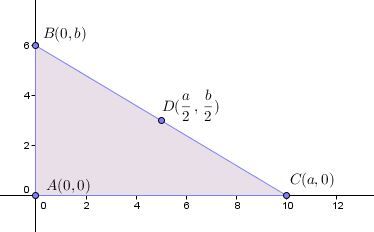
Le mot « équidistant » signifie « à la même distance », donc on cherche à démontrer que le point milieu de l'hypoténuse est à la même distance de tous les sommets d'un triangle rectangle.
La démonstration se déroule comme suit :
|
Hypothèses |
Conclusion |
|---|---|
|
|\triangle ABC| est rectangle en |A.| |
|D| est équidistant des trois sommets du triangle |ABC.| |
|
Affirmations |
Justifications |
|
Les coordonnées de |D| sont |\left(\dfrac{a}{2},\dfrac{b}{2}\right).| |
||\begin{align}(x_m,y_m)&=\left(\dfrac{x_2+x_1}{2},\dfrac{y_2+y_1}{2}\right)\\[3pt]&=\left(\dfrac{0+a}{2},\dfrac{b+0}{2}\right)\\[3pt]&=\left(\dfrac{a}{2},\dfrac{b}{2}\right)\end{align}|| |
|
||\text{dist}(D,C)=\text{dist}(D,B)|| |
||\begin{align}\text{dist}(D,C)&=\sqrt{\left(\dfrac{a}{2}-a\right)^2+\left(\dfrac{b}{2}-0\right)^2}\\[3pt]&=\sqrt{\left(\dfrac{-a}{2}\right)^2+\left(\dfrac{b}{2}\right)^2}\\[3pt]&=\sqrt{\dfrac{a^2}{4}+\dfrac{b^2}{4}}\\[10pt]\text{dist}(D,B)&=\sqrt{\left(\dfrac{a}{2}-0\right)^2+\left(\dfrac{b}{2}-b\right)^2}\\[3pt]&=\sqrt{\left(\dfrac{a}{2}\right)^2+\left(\dfrac{-b}{2}\right)^2}\\[3pt]&=\sqrt{\dfrac{a^2}{4}+\dfrac{b^2}{4}}\end{align}|| |
|
||\text{dist}(D,C)=\text{dist}(D,A)|| |
||\begin{align}\text{dist}(D,C)&=\sqrt{\left(\dfrac{a}{2}-a\right)^2+\left(\dfrac{b}{2}-0\right)^2}\\[3pt]&=\sqrt{\left(\dfrac{-a}{2}\right)^2+\left(\dfrac{b}{2}\right)^2}\\[3pt]&=\sqrt{\dfrac{a^2}{4}+\dfrac{b^2}{4}}\\[10pt]\text{dist}(D,A)&=\sqrt{\left(\dfrac{a}{2}-0\right)^2+\left(\dfrac{b}{2}-0\right)^2}\\[3pt]&=\sqrt{\left(\dfrac{a}{2}\right)^2+\left(\dfrac{b}{2}\right)^2}\\[3pt]&=\sqrt{\dfrac{a^2}{4}+\dfrac{b^2}{4}}\end{align}|| |
|
|D| est équidistant des trois sommets. |
||\begin{gather}\text{dist}(D,C)=\sqrt{\dfrac{a^2}{4}+\dfrac{b^2}{4}}\\[10pt]\text{dist}(D,B)=\sqrt{\dfrac{a^2}{4}+\dfrac{b^2}{4}}\\[10pt]\text{dist}(D,A)=\sqrt{\dfrac{a^2}{4}+\dfrac{b^2}{4}}\\[10pt]\text{dist}(D,C)=\text{dist}(D,B)=\text{dist}(D,A)\end{gather}|| |