Matières
Niveaux
La distance d’un point à une droite correspond à la longueur du plus court segment séparant le point de la droite.
Pour déterminer la distance qui sépare un point d'une droite, il faut déterminer la longueur du segment qui joint perpendiculairement le point à la droite.
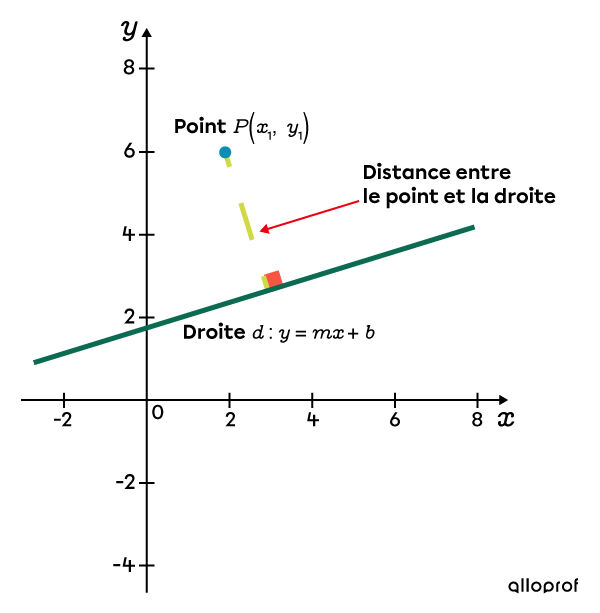
Si on connait l'équation de la droite et les coordonnées du point, on peut trouver la distance qui les sépare en effectuant les étapes suivantes.
Tracer une droite perpendiculaire à la droite donnée et passant par le point |P.|
Déterminer la pente de cette droite : il s'agit de l'opposée de l'inverse de la pente de la droite |d.|
Remplacer |x| et |y| par les coordonnées de |P| pour calculer l'ordonnée à l'origine de la perpendiculaire.
Remplacer le |m| et le |b| trouvés pour obtenir la règle complète de la droite perpendiculaire.
Utiliser la méthode de comparaison pour trouver le point d'intersection entre |d| et la perpendiculaire (voir résoudre un système d’équations au besoin).
Appliquer la formule de la distance entre deux points pour trouver la distance entre le point |P| et la droite |d.|
Quelle est la distance entre la droite |d| d’équation |y = -2x+7| et le point P dont les coordonnées sont |(6,4)|?
Ces nombreuses étapes peuvent être simplifiées par l'utilisation d'une formule permettant de calculer la distance entre un point et une droite.
Équation de forme fonctionnelle :
Soit un point |P(x_1, y_1)| et une droite |d| d’équation |y = mx + b.| La formule à utiliser est la suivante.
||\text{dist}(d,P) = \dfrac{\mid mx_1 - y_1 + b \mid}{\sqrt{m^2 + 1}}||
Équation de forme générale :
Soit un point |P(x_1,y_1)| et une droite |d| d'équation |Ax + By + C = 0.| La formule à utiliser est la suivante.
||\text{dist}(d,P) = \dfrac{\mid Ax_1 + By_1 + C \mid}{\sqrt{A^2 + B^2}}||

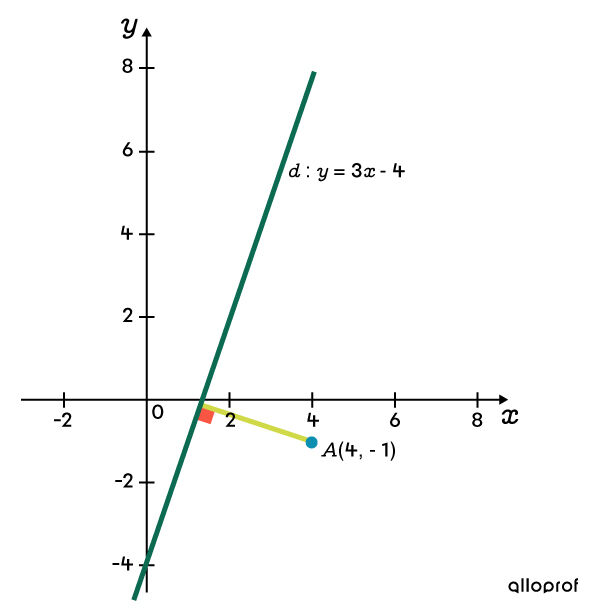
Quelle est la distance entre la droite d’équation |y = 3x-4| et le point |P| dont les coordonnées sont |(4 , -1)|?