Matières
Niveaux
Lorsqu’on étudie les probabilités, on le fait habituellement dans le contexte d’un tirage avec ou sans remise d’un jeu de cartes, d’un dé, etc. Il est également possible de le faire à l’aide de la géométrie en faisant appel à différents rapports. C’est ce qu’on appelle les probabilités géométriques.
Une probabilité géométrique est un rapport de longueurs, d’aires ou de volumes entre une partie d’une figure géométrique et la figure entière.
Pour calculer des probabilités géométriques, il faut connaitre les formules de périmètre, d’aire et de volume.
Remarque : Dans tous les exemples de la fiche, on considère que la probabilité d’atteindre un endroit particulier de la figure est égale à celle d’atteindre n’importe quel autre endroit de cette même figure.

Lorsqu’on souhaite calculer la probabilité qu’une partie d’un objet à 1 dimension (une ligne, un périmètre, etc.) soit atteinte ou choisie, on utilise les rapports de longueurs. La probabilité d’un évènement |(A)| se calcule de la façon suivante.
|P(A)=\dfrac{\text{Longueur à choisir ou à atteindre}}{\text{Longueur totale}}|
Un joueur de soccer botte aléatoirement un ballon vers le fond du terrain représenté ci-dessous. Le ballon reste en tout temps à la hauteur du sol.
Quelle est la probabilité d'atteindre le but?
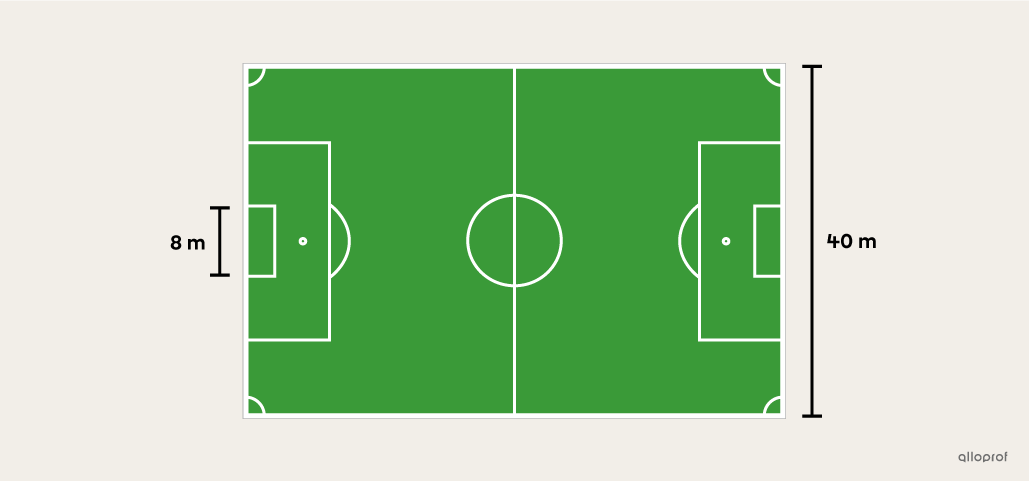
||\begin{align}P(\text{but})&=\dfrac{\text{Longueur à atteindre}}{\text{Longueur totale}}\\&=\dfrac{8\ \text{m}}{40\ \text{m}}\\&=0{,}2\end{align}||
Réponse : La probabilité d’atteindre le but est égale à |0{,}2,| soit |20\ \%.|
Un automobiliste souhaite stationner sa voiture dans une rue qui contient 2 bornes-fontaines placées comme sur le schéma ci-dessous. Il veut placer sa voiture du côté de la rue où sont placées les bornes-fontaines, mais il sait qu’il est interdit de se stationner à moins de 5 mètres de l’une d’elles. Si l’automobiliste choisit un emplacement aléatoirement, quelle est la probabilité que l’extrémité avant de sa voiture soit dans une partie de la rue où le stationnement est interdit?
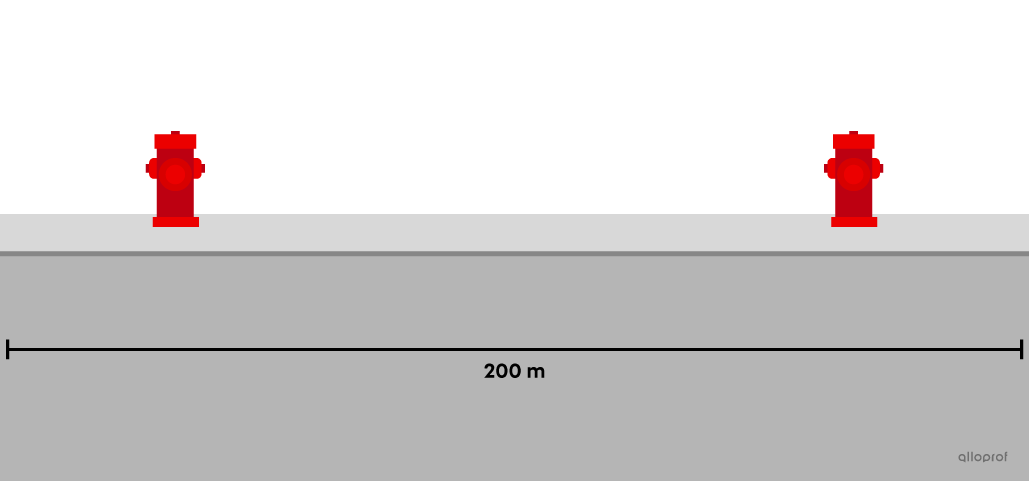
Il est également possible de calculer des probabilités à l’aide de rapports de périmètres.
Des pièces de forme identique servant à former le contour de 2 casse-têtes ont été mélangées. Le 1er casse-tête, une fois terminé, a les dimensions suivantes : |50\ \text{cm}| de longueur par |30\ \text{cm}| de largeur. Le 2e casse-tête mesure |70\ \text{cm}| par |60\ \text{cm}.| Quelle est la probabilité que la première pièce choisie au hasard appartienne au 1er casse-tête?
Lorsqu’on souhaite calculer la probabilité qu’une partie d’un objet en 2 dimensions soit atteinte ou choisie, on peut utiliser les rapports d’aires. La probabilité de l’évènement |A| se calcule de la façon suivante.
|P(A)=\dfrac{\text{Aire choisie ou à atteindre}}{\text{Aire totale}}|
On lance un dard dans le carré suivant. Quelle est la probabilité d’atteindre le disque?

On doit tout d’abord calculer l’aire du carré.||\begin{align}A_{\text{carré}}&=c^2\\&=5^2\\&=25\ \text{cm}^2\end{align}||On calcule ensuite l’aire du disque.||\begin{align}A_{\text{disque}}&=\pi r^2\\&=\pi \left(\dfrac{5}{2}\right)^2\\&\approx19{,}63\ \text{cm}^2\end{align}||On peut finalement calculer la probabilité d’atteindre le disque avec le dard.||\begin{align}P(\text{disque})&=\dfrac{A_{\text{disque}}}{A_{\text{carré}}}\\&=\dfrac{19{,}63\ \text{cm}^2}{25\ \text{cm}^2}\\&\approx 0{,}79\end{align}||Réponse : La probabilité d’atteindre le disque est d’environ |0{,}79,| soit |79\ \%.|
On lance un dard sur la figure suivante.

Quelle est la probabilité d’atteindre une partie bleue ou une partie jaune?
Lorsqu’on souhaite calculer la probabilité qu’une partie d’un objet en 3 dimensions soit atteinte ou choisie, on peut utiliser les rapports de volumes. La probabilité de l’évènement |A| se calcule de la façon suivante.
|P(A)=\dfrac{\text{Volume choisi ou à atteindre}}{\text{Volume total}}|
On place une cerise au fond d’un pichet contenant |1\ \text{L}| de jus d’orange. Une personne se sert un verre de jus de forme cylindrique rempli jusqu’au bord. Le verre a |10\ \text{cm}| de haut et |3\ \text{cm}| de rayon. Quelle est la probabilité que le verre de jus de la personne contienne la cerise?

||P(\text{cerise})=\dfrac{V_\text{verre}}{V_\text{total du pichet}}||Il est important de savoir qu’une capacité de |1\ \text{L}| est égale à |1\ \text{dm}^3.| Le volume de jus contenu dans le pichet est donc égal à |1\ \text{dm}^3,| soit |1\ 000\ \text{cm}^3.|
On calcule le volume du verre.||\begin{align}V_{\text{verre}}&=\pi r^2\times h\\&=\pi(3)^2\times 10\\&=90\pi\\&\approx282{,}74\ \text{cm}^3\end{align}||On calcule maintenant la probabilité.||\begin{align}P(\text{cerise})&=\dfrac{V_{\text{verre}}}{V_\text{total du pichet }}\\&=\dfrac{282{,}74\ \text{cm}^3}{1\ 000\ \text{cm}^3}\\&\approx 0{,}28\end{align}||Réponse : La probabilité que le verre de jus contienne la cerise est d’environ |28\ \%.|
Lorsqu’on souhaite calculer la probabilité qu’une partie d’un objet soit atteinte ou choisie et qu’on connait au moins un angle, on peut utiliser les rapports de mesures d’angles. La probabilité de l’évènement |A| se calcule de la façon suivante.
|P(A)= \dfrac{\text{Angle délimitant la partie choisie}}{\text{Angle délimitant l'objet en entier}}|
On prépare une pizza. Il ne reste qu’une seule olive, mais on décide tout de même de la placer sur la pizza. Une fois le repas terminé, on coupe 2 morceaux délimités par un angle au centre de |60^\circ.|
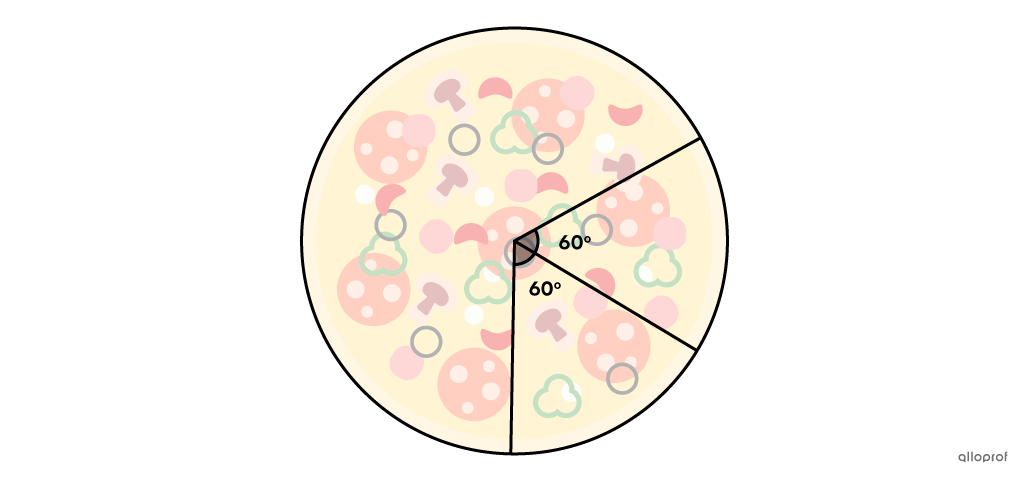
Quelle est la probabilité que l’olive se situe sur l’une des 2 pointes coupées?
L’angle formé par la pizza entière est égal à |360^\circ,| puisqu’elle forme un disque complet. Lorsqu’on coupe le 1er morceau, on le fait selon un angle au centre de |60^\circ.| Au cours de la 2e coupe, on prend un morceau formant un autre angle de |60^\circ.| On a donc coupé une partie de la pizza délimitée par un angle total de |120^\circ.|||\begin{align}P(\text{Olive})&=\dfrac{\text{Angle total des 2 pointes de pizza}}{\text{Angle formé par la pizza entière}}\\&=\dfrac{120^\circ}{360^\circ}\\&=\dfrac{1}{3}\end{align}||Réponse : La probabilité qu’une des 2 personnes ait l’olive sur sa pointe de pizza est de |\dfrac{1}{3},| soit environ |33\ \%.|
Lorsqu’on souhaite calculer une probabilité à l’aide de données prises dans un plan cartésien, il faut faire attention en lisant la question. Il s’agit parfois d’un rapport de longueurs ou d’un rapport d’aires.
Dans un plan cartésien, on peut observer un segment qui débute au point |(0,6)| et qui se termine au point |(10,0).| Ce segment passe par le centre d’un disque situé au point |(5,3).| Le point |(7,4)| est un point sur le cercle. On choisit un point au hasard sur la droite. Quelle est la probabilité qu’il soit à l’intérieur du cercle?
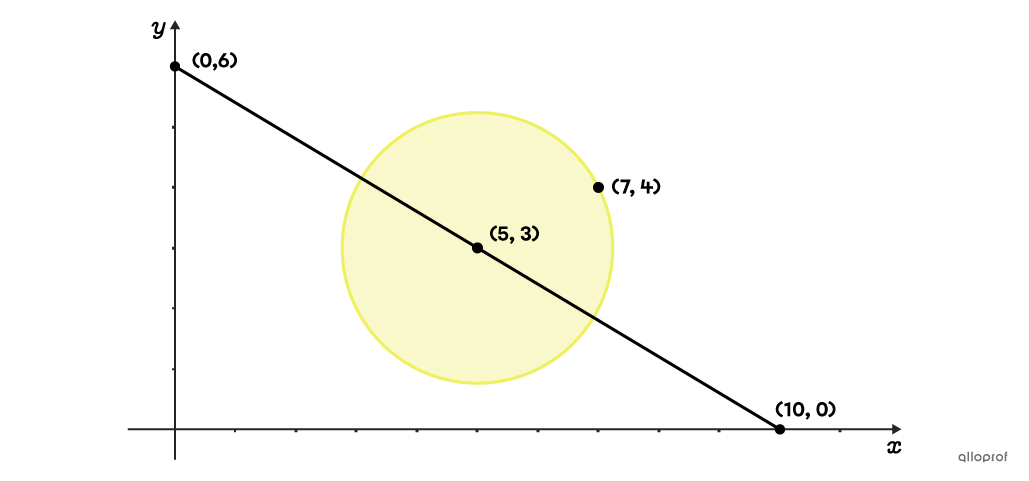
La probabilité recherchée implique un rapport de longueurs.||P(\text{cercle}) = \dfrac{\text{Diamètre du cercle}}{\text{Longueur du segment}}||On calcule d’abord la longueur du segment qui relie les points |(0,6)| et |(10,0)| en se servant de la formule de la distance entre 2 points.||\begin{align}d&=\sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2}\\&=\sqrt{(10 - 0)^2 + (0 -6)^2}\\&=\sqrt{100+36}\\&=\sqrt{136}\\&\approx11{,}66\end{align}||La longueur totale du segment est d’environ |11{,}66| unités.
On doit ensuite trouver la longueur du diamètre du cercle. On peut y arriver en trouvant la mesure de son rayon à l’aide des points |(5,3)| et |(7,4).|||\begin{align}d&=\sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2}\\&=\sqrt{(7 - 5)^2 + (4 - 3)^2}\\&=\sqrt{2^2 + 1^2}\\&=\sqrt{5}\\&\approx2{,}24\end{align}||Comme la longueur du rayon est d’environ |2{,}24| unités, la longueur du diamètre est de |2{,}24 \times 2 = 4{,}48| unités.
On peut maintenant calculer la probabilité.||\begin{align}P(\text{cercle})&= \dfrac{\text{Diamètre du cercle}}{\text{Longueur du segment}}\\ &=\dfrac{4{,}48}{11{,}66}\\&\approx0{,}38\end{align}||La probabilité qu’un point choisi aléatoirement sur le segment soit également à l’intérieur du cercle est d’environ |0{,}38,| soit |38\ \%.|