Matières
Niveaux
Un évènement est un sous-ensemble de l'univers des résultats possibles d'une expérience aléatoire.
Les éléments qui appartiennent à un tel sous-ensemble sont appelés les résultats (ou cas) favorables à la réalisation de l'évènement.
Lors d'une expérience aléatoire, on peut faire une prédiction par rapport à un évènement futur encore inconnu, mais qui a une chance de se produire.
On peut s’intéresser à plusieurs évènements lors du lancer d’un dé à |6| faces numérotées de |1| à |6.| Dans un tel cas, l’univers des résultats possibles est |\Omega=\{1,2,3,4,5,6\}.|
|
Exemple d’évènement |
Cas favorables à l’évènement |
|---|---|
|
|A :| Obtenir un |3.| |
|A=\{3\}| |
|
|B :| Obtenir un nombre impair. |
|B=\{1,3,5\}| |
|
|C :| Obtenir un nombre plus grand que |4.| |
|C=\{5,6\}| |
|
|D :| Obtenir un nombre premier. |
|D=\{2,3,5\}| |
Remarque : On désigne toujours un évènement à l'aide d'une lettre majuscule.
Un évènement peut correspondre à un seul résultat, à plusieurs résultats ou à tous les résultats de l'univers des possibles. Il peut aussi ne correspondre à aucun résultat. On distingue ainsi différents types d'évènements.

Un évènement élémentaire est un évènement qui ne contient qu'un seul résultat de l'univers des possibles.
On choisit une carte dans un jeu de 52 cartes. L’évènement « obtenir le 2 de pique » est un évènement élémentaire, car il ne contient qu'un seul résultat de l'univers des possibles. La probabilité de cet évènement est de |\dfrac{1}{52}.|
L'évènement « obtenir un 3 » lorsqu'on lance un dé à |6| faces est un évènement élémentaire, car il ne contient qu'un seul résultat de l'univers des possibles. La probabilité de cet évènement est de |\dfrac{1}{6}.|
La somme des probabilités de tous les évènements élémentaires d'une expérience aléatoire est égale à |1,| c’est-à-dire |100\ \%.|
Un évènement certain est un évènement qui se produit toujours. Il correspond à l'univers des résultats possibles et sa probabilité est de |100\ \%.|
Un évènement possible (ou probable) est un évènement qui peut se produire. Il correspond à un sous-ensemble non vide de l’univers des résultats possibles et sa probabilité est entre |0\ \%| et |100\ \%.|
Un évènement impossible est un évènement qui ne peut pas se produire. Il ne correspond à aucun des résultats de l’univers des possibles et sa probabilité est de |0\ \%.|
On peut illustrer les évènements certains, possibles et impossibles sur une ligne des probabilités. Sur cette ligne, plus un résultat est situé à gauche, moins il a de chances de se produire.

Voici quelques exemples pour des évènements liés à l'expérience « lancer un dé à 6 faces ».

L'évènement « obtenir une bille rouge » lorsqu'on pige une bille dans un sac contenant |3| billes rouges est un évènement certain, car l'évènement correspond à l'univers des résultats possibles. La probabilité de cet évènement est de |\dfrac{3}{3},| soit |1| ou |100\ \%.|
L'évènement « obtenir pile » lorsqu'on lance une pièce de monnaie est un évènement probable, car il correspond à un sous-ensemble non vide de l'univers des possibles. La probabilité de cet évènement est de |\dfrac{1}{2,}| soit |50\ \%.|
L'évènement « obtenir une bille verte » lorsqu'on pige une bille dans un sac contenant |2| billes rouges et |3| billes bleues est un évènement impossible, car il n'y a pas de bille verte dans le sac. La probabilité de cet évènement est de |0.|
Des évènements équiprobables sont des évènements qui ont les mêmes chances de se produire.
L'évènement |A| « obtenir un nombre inférieur à 2 » et l'évènement |B| « obtenir un nombre supérieur à 5 » lorsqu'on tire un dé à |6| faces sont 2 évènements équiprobables, puisqu'ils ont autant de chances de se produire l'un que l'autre. La probabilité de l'évènement |A| est |P(A)=\dfrac{1}{6}| et la probabilité de l'évènement |B| est |P(B)=\dfrac{1}{6},| puisqu'ils n'ont qu'un cas favorable chacun.
L'évènement |C| « obtenir un roi » et l'évènement |D| « obtenir un 5 » lorsqu'on pige une carte dans un jeu de 52 cartes sont 2 évènements équiprobables, puisqu'ils ont autant de chances de se produire l'un que l'autre. La probabilité de l'évènement |C| est |P(C)=\dfrac{1}{13}| et la probabilité de l'évènement |D| est |P(D)=\dfrac{1}{13},| puisqu'ils ont |4| cas favorables chacun sur un total de |52.|
Il est possible de comparer les probabilités de plusieurs évènements.
Un évènement est moins probable lorsqu'il a moins de chances de se produire qu'un autre évènement.
Un évènement est plus probable lorsqu'il a plus de chances de se produire qu'un autre évènement.
L'évènement |A| « piger une carte de carreau » dans un jeu de 52 cartes est plus probable que l'évènement |B| « piger une dame », puisqu'il a plus de chances de se produire. En effet, la probabilité de l'évènement |A| est |P(A)=\dfrac{13}{52}| alors que la probabilité de l'évènement |B| est |P(B)=\dfrac{4}{52}.|
On peut également affirmer que l'évènement |B| est moins probable que l'évènement |A,| puisque sa probabilité est inférieure.
Des évènements compatibles sont des évènements qui ont au moins un cas favorable en commun.
Des évènements incompatibles sont des évènements qui n’ont pas de cas favorables en commun.
Pour que 2 évènements |A| et |B| soient compatibles, leur intersection ne doit pas être vide |(A \cap B \neq \varnothing).| Ainsi, il existe au moins un cas favorable commun aux 2 évènements.
À l’inverse, l'intersection entre des évènements incompatibles est vide |(A \cap B = \varnothing).|
On s’intéresse aux 3 évènements suivants lors du lancer d’un dé à 6 faces.
L'évènement |A| « obtenir un nombre pair »;
L'évènement |B| « obtenir un 2, un 3 ou un 5 »;
L’évènement |C| « obtenir 1 ».
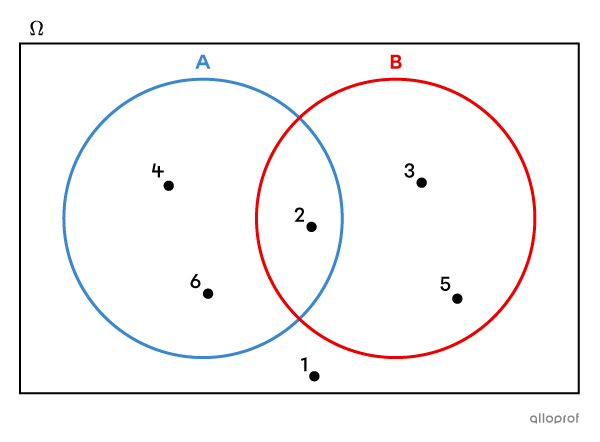
L'évènement |A| et l'évènement |B| sont des évènements compatibles puisque |2| est un cas favorable commun aux 2 évènements |(A \cap B = \{2\}).|
En représentant l’univers des possibles dans un diagramme de Venn, on constate qu'il y a une valeur dans l'intersection de |A| et |B.|
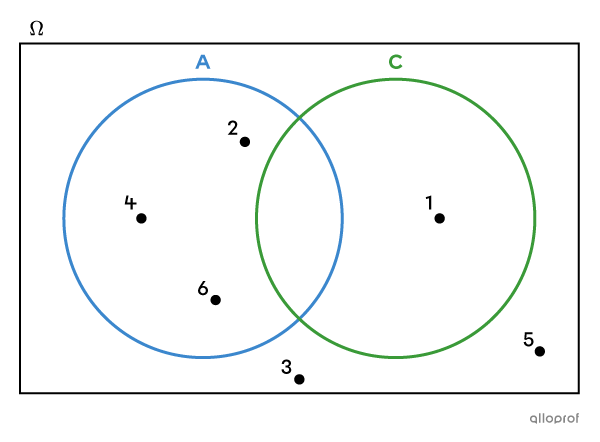
L’évènement |A| et l’évènement |C| sont des évènements incompatibles puisqu'ils n'ont aucun cas favorable en commun.
En représentant l’univers des possibles dans un diagramme de Venn, on constate qu'il n'y a aucun élément dans l'intersection de |A| et |C.|
Lorsque 2 évènements sont compatibles, la probabilité que l'évènement |A| ou l'évènement |B| se produise est |P(A \cup B) = P(A) + P(B) - P(A \cap B).|
On peut utiliser la même formule dans le cas d’évènements incompatibles, mais étant donnée que |P(A\cap B)=0,| la formule devient simplement |P(A \cup B) = P(A) + P(B).|
Des évènements complémentaires sont des évènements incompatibles dont l’union de leurs résultats correspond à l'univers des résultats possibles.
Pour que 2 évènements |A| et |B| soient complémentaires, leur intersection doit être vide |(A \cap B = \varnothing)| et l’union de leurs cas favorables doit être équivalente à l'univers des résultats possibles |(A \cup B = \Omega).|
La somme des probabilités de 2 évènements complémentaires |A| et |B| donne |1,| soit |100\ \%.|||P(A) + P(B) = 1||
Remarque : En général, l'évènement complémentaire à l'évènement |A| est noté |A'| ou |A^c.|
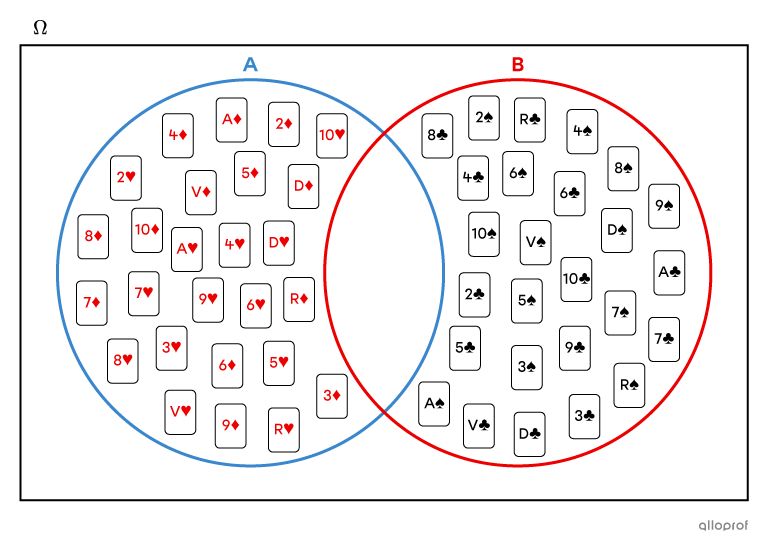
L'évènement |A| « obtenir une carte rouge » et l'évènement |B| « obtenir une carte noire » sont des évènements complémentaires, puisque l’union de leurs cas favorables correspond à l'ensemble des cartes contenues dans un jeu de 52 cartes. La somme des probabilités de ces évènements est égale à |1.|||P(A) + P(B) = \dfrac{26}{52} + \dfrac{26}{52} =\dfrac{52}{52}= 1||
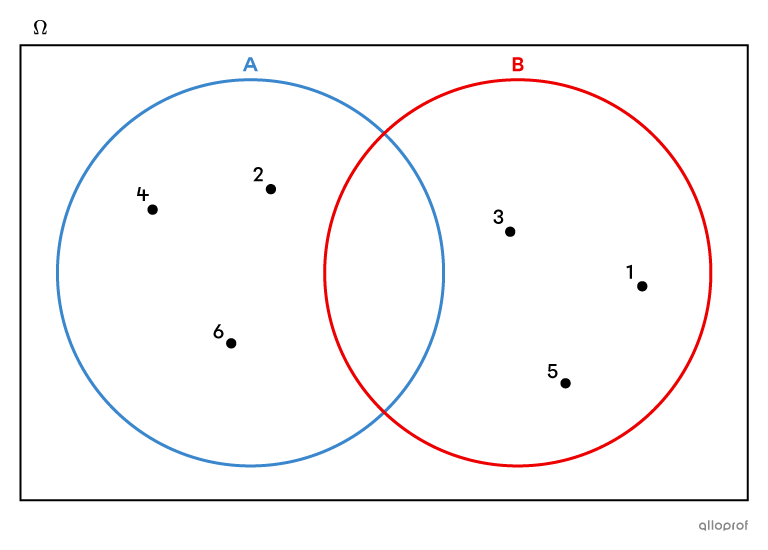
L'évènement |A| « obtenir un nombre pair » et l'évènement |B| « obtenir un nombre impair » lorsqu'on lance un dé à |6| faces sont des évènements complémentaires, puisque l’union de leurs cas favorables correspond à l'ensemble des résultats possibles et qu’aucun élément ne se trouve dans leur intersection.
Lorsqu’on cherche la probabilité d'un évènement |A| et qu’on connait la probabilité de son évènement complémentaire |A',| on peut utiliser la relation |P(A)+P(A')=1| et isoler |P(A).|
On estime que |75\ \%| des élèves de secondaire 2 ne portent pas de lunettes. Sachant cela, quelle est la probabilité qu’un élève de secondaire 2 choisi au hasard porte des lunettes?
Les évènements « porter des lunettes » et « ne pas porter des lunettes » sont des évènements complémentaires. En effet, leur intersection est vide, puisqu’un élève ne peut pas porter des lunettes et ne pas les porter simultanément. Aussi, comme « porter des lunettes » et « ne pas porter des lunettes » sont les 2 seules options possibles, l’union de ces ensembles contient tous les éléments de l’univers des possibles. On a donc |P(A)+P(A')=1.|||\begin{align}P(\text{lunettes}) + P(\text{pas de lunettes})&=1\\P(\text{lunettes})&=1-P(\text{pas de lunettes})\\&=1-0{,}75\\&=0{,}25\end{align}||
Réponse : La probabilité qu’un élève de secondaire 2 choisi au hasard porte des lunettes est de |25\ \%.|
Remarque : Posséder une certaine caractéristique et ne pas posséder cette même caractéristique sont toujours des évènements complémentaires.
Des évènements dépendants sont des évènements dont la réalisation de l'un affecte la réalisation de l'autre.
Des évènements indépendants sont des évènements dont la réalisation de l'un n'influence pas la réalisation de l'autre.
Il est souvent question d’évènements indépendants lors d'une expérience aléatoire à plusieurs étapes avec remise. Dans les expériences sans remise, il s’agit plutôt d’évènements dépendants.
Lorsqu'on lance un dé à |2| reprises, la probabilité d'obtenir un |3| au 2e lancer n'est pas affectée par la probabilité d'obtenir un |5| au 1er lancer, puisque les |2| tirages sont des évènements indépendants.
Par contre, toujours lorsqu’on lance un dé à |2| reprises, la probabilité d’obtenir une somme de |10| est influencée par le résultat du 1er lancer. En effet, si on obtient un |1| au 1er lancer, il est alors impossible d’obtenir une somme de |10,| tandis que si on obtient un |5| au 1er lancer, c’est encore possible d’avoir une somme de |10.|
On tire |2| cartes sans remise d'un jeu de 52 cartes. Comme il n'y a pas de remise, le 2e évènement est influencé par le 1er puisqu'il n'y a plus que |51| cartes dans le jeu après le 1er évènement. La probabilité du 2e évènement est donc dépendante du 1er évènement.
La probabilité de la réalisation consécutive des évènements indépendants |A| et |B| est donnée par |P(A \cap B) = P(A) \times P(B).| On appelle cette propriété le principe de multiplication.
De la même façon, lors d'une expérience aléatoire à plusieurs étapes, si les évènements |A| et |B| sont dépendants, alors on a |P(A \cap B) \neq P(A) \times P(B).|
Des évènements mutuellement exclusifs sont des évènements qui n’ont aucun cas favorable en commun |(A \cap B = \varnothing).|
Des évènements non mutuellement exclusifs sont des évènements qui ont au moins un cas favorable en commun |(A \cap B \neq \varnothing).|
Lorsque 2 évènements sont non mutuellement exclusifs, la probabilité de l'évènement |A| ou de l'évènement |B| est |P(A \cup B) = P(A) + P(B) - P(A \cap B).|
On peut utiliser la même formule dans le cas d’évènements mutuellement exclusifs, mais étant donnée que |P(A\cap B)=0,| la formule devient simplement |P(A \cup B) = P(A) + P(B).|
On pige une carte dans un jeu de 52 cartes. L'évènement |A| « obtenir un cœur » et l'évènement |B| « obtenir une carte noire » sont des évènements mutuellement exclusifs car ils n’ont aucun élément en commun. En effet, une carte ne peut pas à la fois être un cœur et être noire.
On pige une carte dans un jeu de 52 cartes. L'évènement |A| « obtenir un roi » et l'évènement |B| « obtenir une carte noire » sont des évènements non mutuellement exclusifs car ils ont des cas favorables en commun : les rois de pique et de trèfle sont à la fois des rois et des cartes noires.
On lance |2| dés à |6| faces et on fait la somme des résultats obtenus.
L’évènement |A| « obtenir une somme de 2 » est un évènement élémentaire, car il ne contient qu'un seul résultat de l'univers des possibles : |A=\{(1,1)\}.|
L’évènement |B| « obtenir une somme inférieure à 15 » est un évènement certain, car il contient tous les résultats de l'univers des possibles puisqu'il se produit toujours. En effet, la somme de |2| dés à |6| faces est toujours située entre |2| et |12| inclusivement.
L’évènement |C| « obtenir une somme de 15 » est un évènement impossible, car il ne contient aucun résultat de l'univers des possibles. En effet, la plus grosse somme possible avec |2| dés à |6| faces est de |12|.
Les évènements |D| « obtenir une somme de 12 » et |A| « obtenir une somme de 2 » sont équiprobables, car les |2| ont la même probabilité de se produire. En effet, les |2| évènements n’ont qu’un seul résultat favorable. |A=\{(1,1)\}| et |D=\{(6,6)\}.|
L’évènement |E| « obtenir une somme de 4 » est plus probable que l’évènement |A| « obtenir une somme de 2 ». En effet, il y a |3| résultats favorables à l’évènement |D,| qui sont |\{(1,3), (2,2), (3,1)\},| alors qu’un seul résultat est favorable à l’évènement |A.|
Les évènements |F| « obtenir au moins un 2 » et |A| « obtenir une somme de 2 » sont incompatibles car il n’ont pas de résultats favorables en commun.
Les évènements |G| « obtenir une somme supérieur à 2 » et |A| « obtenir une somme de 2 » sont complémentaires, car ils sont incompatibles et que l’union de leurs résultats correspond à l'univers des résultats possibles.
Les évènements |H| « obtenir une somme de 8 » et |F| « obtenir au moins un 2 » sont dépendants, car la réalisation de l'un influence la réalisation de l'autre.