Matières
Niveaux
Résoudre un problème d'optimisation
Fiche | Mathématiques
Secondaire
5
Lorsqu’on résout un problème d’optimisation, on cherche la solution qui maximise ou minimise la fonction à optimiser qui, elle, est déterminée selon un objectif. On le fait en respectant des contraintes qui sont représentées sous la forme d’un système d’inéquations. Dans le plan cartésien, ces inéquations forment un polygone de contraintes et l’un des sommets de ce polygone correspond à la solution recherchée.
Les étapes de résolution d'un problème d'optimisation
-
Identifier les variables.
Pour déterminer les variables, on doit s’intéresser aux éléments qui varient et non à l’élément qu’on cherche à optimiser. Dans les problèmes étudiés au secondaire, il y a toujours 2 variables seulement.
-
Traduire les contraintes par un système d'inéquations.
Chaque contrainte est associée à une seule inéquation. De plus, si les variables représentent des quantités qui ne peuvent pas être négatives, on doit poser les contraintes de positivité (non-négativité). Voici un tableau contenant quelques expressions qu’on retrouve régulièrement dans les contraintes ainsi que les inégalités qu’elles représentent.
|
Symbole |
Mots-clés |
|---|---|
|
|x<y| |
|x| est plus petit que |y,| |x| est inférieur à |y,| |x| vaut (strictement) moins que |y,| etc. |
|
|x\leq y| |
|x| est plus petit ou égal à |y,| |x| est inférieur ou égal à |y,| |x| ne doit pas dépasser |y,| |x| est au maximum égal à |y,| |x| vaut au plus autant que |y,| etc. |
|
|x>y| |
|x| est plus grand que |y,| |x| est supérieur à |y,| |x| doit dépasser |y,| |x| vaut (strictement) plus que |y,| etc. |
|
|x\geq y| |
|x| est plus grand ou égal à |y,| |x| est supérieur ou égal à |y,| |x| est au minimum égal à |y,| |x| vaut au moins autant que |y,| etc. |
-
Établir la règle de la fonction à optimiser |\boldsymbol{(z).}|
La fonction à optimiser s'écrit sous la forme |z=ax+by+c,| où |x| et |y| sont les variables et où |z| représente la quantité qu’on cherche à maximiser ou à minimiser. Il arrive souvent que |z| représente un cout ou un revenu. Dans ces cas, il est possible d’utiliser une autre variable, comme |C| ou |R.|
-
Tracer le polygone de contraintes.
Pour y arriver, on doit représenter toutes les inéquations dans le plan cartésien. Le polygone de contraintes représente la région du plan cartésien qui contient l’intersection des ensembles-solutions de toutes les inéquations.
-
Déterminer les coordonnées des sommets du polygone de contraintes.
Pour déterminer les coordonnées d’un sommet, on doit prendre les équations des 2 droites frontières qui forment ce sommet et résoudre le système d’équations. Pour y arriver, on peut utiliser la méthode de comparaison, la méthode de substitution ou la méthode de réduction.
-
Trouver le sommet optimal (avec un tableau ou une droite baladeuse).
Il faut remplacer |x| et |y| dans la fonction à optimiser par chaque couple déterminé à l’étape précédente. Il peut être utile de se faire un tableau pour compiler les résultats. On peut aussi utiliser la droite baladeuse pour réduire le nombre de sommets à évaluer. Il faut analyser les différentes valeurs de |z| et déterminer laquelle est la plus avantageuse selon notre objectif.
-
Donner une réponse complète.
Pour répondre à la question, on doit écrire une phrase complète dans laquelle on retrouve le couple |(x,y)| qui maximise ou minimise la fonction, ainsi que la valeur de |z| associée à ce couple.
La droite baladeuse
Il existe une façon de réduire le nombre de sommets à évaluer pour trouver la solution optimale. Il s’agit de la technique de la droite baladeuse.
La droite baladeuse est une droite de pente |-\dfrac{a}{b}| qui se « balade » dans le plan cartésien, où |a| et |b| sont les paramètres de la fonction à optimiser |(z=ax+by+c).|
Lorsqu'on glisse la droite baladeuse dans le plan cartésien, le premier et le dernier sommet du polygone de contraintes que cette droite touche sont les points qui vont soit minimiser, soit maximiser la situation.
Dans l'animation ci-dessous, tu peux modifier les paramètres |a| et |b| de la fonction à optimiser à l'aide des curseurs. Tu peux également déplacer les sommets du polygone de contraintes et glisser la droite baladeuse. Pour cela, tu n'as qu'à déplacer le point vert qui est placé sur la droite baladeuse. Tu remarqueras que, lorsqu'on déplace une droite baladeuse, celle-ci garde toujours la même pente.
Pour valider ta compréhension à propos des problèmes d'optimisation de façon interactive, consulte la MiniRécup suivante.
Des exemples de problème d'optimisation
Voici un exemple complet de résolution d’un problème d’optimisation. Dans ce problème, la solution optimale est déterminée à l’aide d’un tableau.
Mélanie gagne sa vie grâce à son troupeau de |30| chèvres qui produisent chacune au plus |20| litres de lait par semaine. Elle utilise ce lait pour créer |2| produits qu’elle vend ensuite au marché : le yogourt et la crème.
Il faut |1{,}5\ \text{L}| de lait pour faire |1\ \text{L}| de yogourt. Il faut aussi |6\ \text{L}| de lait pour produire |1\ \text{L}| de crème.
Compte tenu de la demande pour ses produits, Mélanie doit produire au moins |3| fois plus de yogourt que de crème et elle doit produire au moins |200\ \text{L}| de yogourt par semaine.
Au marché, elle vend son yogourt |36\ $| le litre et sa crème, |10\ $| le litre.
Combien de litres de yogourt et de litres de crème Mélanie doit-elle produire par semaine si elle désire maximiser ses revenus?
Voir la solution
Dans ce 2e exemple, on ajoute une contrainte. Cela consiste à ajouter une nouvelle inéquation qui va changer le polygone de contraintes.
Victor est vendeur de planches à roulettes. Il vend ses planches professionnelles |300\ $| et ses planches standards |50\ $.| À cause de ses finances et de la grandeur de son magasin, il doit respecter certaines contraintes quant à la quantité de planches à roulettes offertes. Le polygone ci-dessous illustre ces contraintes.
|x :| nombre de planches professionnelles
|y :| nombre de planches standards
Victor veut faire une grande vente au cours de la prochaine fin de semaine. Jean-Luc, son conseiller aux ventes, lui suggère d'avoir au plus |80| planches professionnelles dans son magasin.
Est-ce que Victor devrait suivre le conseil de Jean-Luc?
Voir la solution
Les cas particuliers
Au moment de déterminer une solution optimale pour une situation, il est possible de tomber sur des cas particuliers.
Le sommet optimal n’est pas sur une ligne pleine
Lorsque des inéquations de contraintes comportent les symboles d’inégalité stricte |<| ou |>,| les droites ne sont pas incluses dans l’ensemble-solution. Sur le graphique, on a une ligne pointillée. Si le sommet qui optimise la fonction est sur une ou plusieurs droites pointillées, on doit rejeter cette solution, puisqu’elle ne respecte pas toutes les contraintes. Il faut donc tester les points près de ce sommet qui font partie de l’ensemble-solution et choisir le meilleur.
La solution doit avoir une ou des coordonnées entières
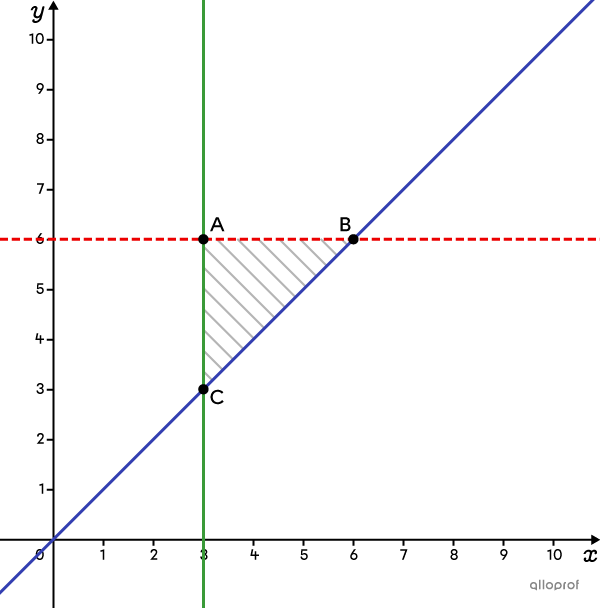
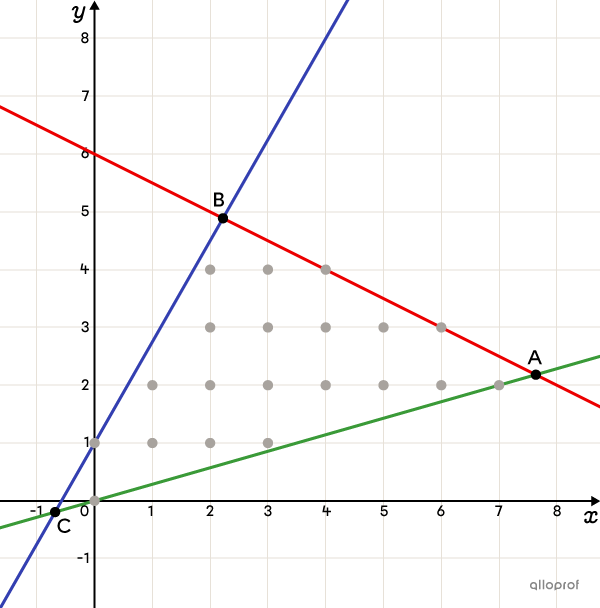
Selon le contexte, il arrive que les valeurs de |x| et |y| soient des nombres entiers. C’est le cas, par exemple, lorsque |x| et |y| représentent un nombre d’objets, d’animaux ou de personnes. Par contre, les coordonnées des sommets du polygone de contraintes ne sont pas nécessairement entières. Si c’est le cas, il faut alors choisir le point ayant des coordonnées entières et faisant partie de l’ensemble-solution qui optimise la situation.
Dans l’exemple suivant, ni le sommet |A| ni le sommet |B| n’ont des coordonnées entières. Si |A| est le sommet qui optimise la fonction |z,| alors le point à coordonnées entières qui est la solution optimale et qui respecte le contexte est le couple |(7,2)| ou le couple |(6,3).|
La solution est un côté du polygone de contraintes
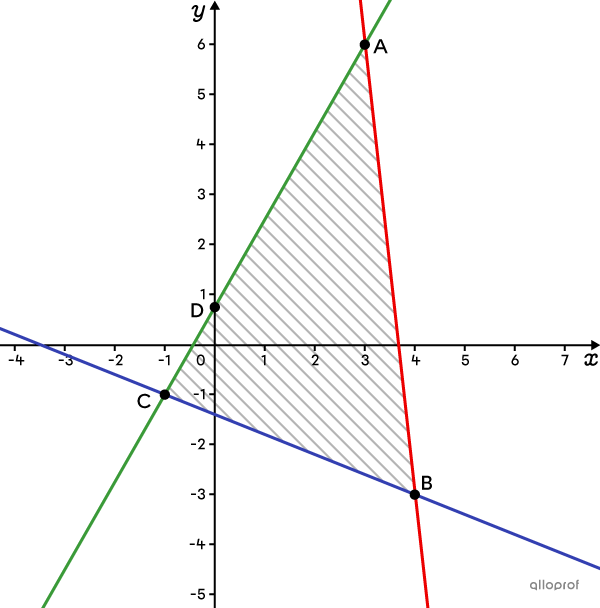
Il arrive que 2 sommets du polygone optimisent la fonction et donnent la même valeur de |z.| Lorsque c’est le cas, cela signifie que tous les points situés sur le segment qui relie ces 2 sommets sont des solutions optimales. Il y a donc plusieurs réponses possibles.
Dans l’exemple suivant, les sommets |A(3,6)| et |C(-1,-1)| maximisent tous les 2 la fonction avec une valeur |z| de |3.| Ainsi, tous les points sur le segment |\overline{AC}| l’optimisent également. Le point |D(0;0{,}75)| en est la preuve, car il donne aussi un |z| de |3.|
|
Sommet du polygone |
Règle d'optimisation |
Valeur de |\boldsymbol{z}| |
|---|---|---|
|
|A(3,6)| |
|z=-7(3)+4(6)| |
|3| |
|
|B(4,-3)| |
|z=-7(4)+4(-3)| |
|-40| |
|
|C(-1,-1)| |
|z=-7(-1)+4(-1)| |
|3| |
|
|D(0; 0{,}75)| |
|z=-7(0)+4(0{,}75)| |
|3| |
Il y a plus d’une fonction à optimiser
Lorsqu’une situation a plusieurs solutions optimales, il arrive que la mise en situation fournisse une fonction à optimiser supplémentaire. Cela permet d’éliminer certaines des solutions et de trouver celle qui optimise les 2 fonctions.
Dans l’exemple suivant, il y a 2 fonctions à optimiser. Il faut alors commencer par trouver les solutions qui maximisent la quantité de vivres à acheminer. À partir de ces solutions, on peut ensuite déterminer celle qui minimise le cout d’achat.
On transporte des vivres pour des sinistrés dans 2 sortes de contenants : des sacs et des caisses.
Le polygone ci-dessous représente les contraintes associées au nombre de sacs et au nombre de caisses qu’il est possible d’utiliser.
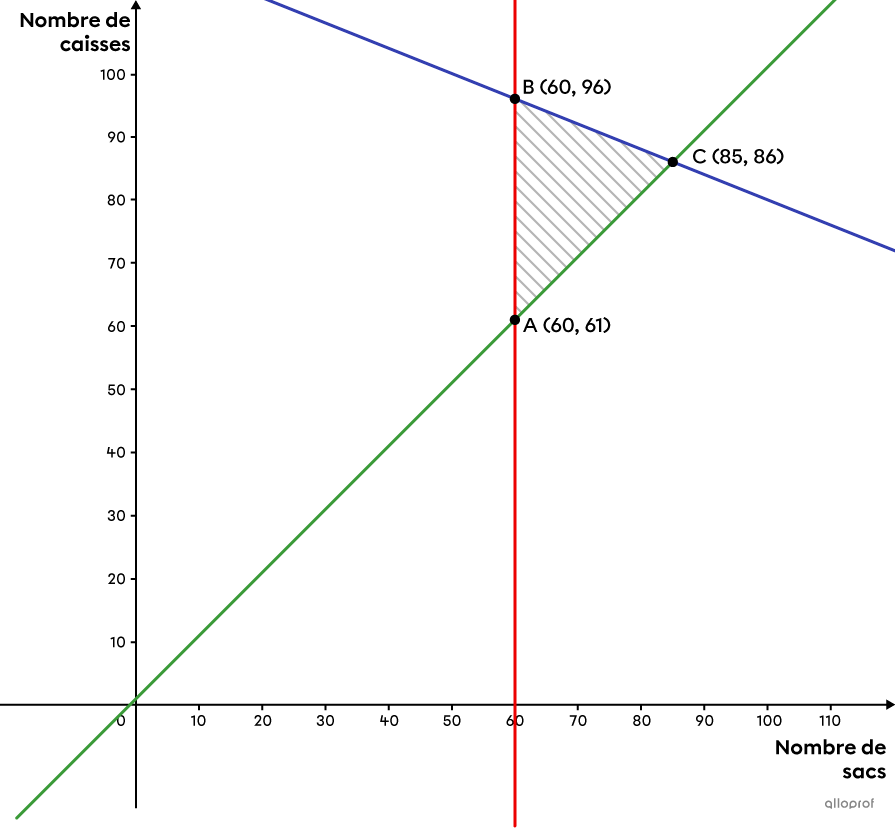
Chaque sac permet de transporter |10\ \text{kg}| de vivres et chaque caisse permet d'en transporter |25\ \text{kg}.| On veut maximiser la quantité de vivres à acheminer aux sinistrés. Par ailleurs, on peut se procurer des sacs pour |2\ \$| chacun et des caisses pour |8\ \$| chacune. On veut également minimiser les dépenses reliées à l'achat de ces contenants.