Matières
Niveaux
Pour tracer une fonction logarithmique, on remplace |x| dans la règle par différentes valeurs afin de déterminer les valeurs de |y| correspondantes. Pour y arriver, il est important de connaitre les lois des logarithmes.
La fonction logarithmique possède une asymptote verticale et son domaine est restreint. Ainsi, tous les points appartenant à la courbe sont situés soit à gauche, soit à droite de l’asymptote. Avant de la tracer, on doit donc vérifier de quel côté est située la courbe en analysant le paramètre |b| de la règle.
Si le paramètre |b| est positif, la courbe est située à droite de l’asymptote.
Si le paramètre |b| est négatif, la courbe est située à gauche de l’asymptote.
On s’intéresse à 2 types de règles.
Il est important de noter que le logarithme népérien |(\ln x)| se trace de la même façon que les autres fonctions logarithmiques, sauf que la base est le nombre |e.|
||\ln x=\log_ex||où||e\approx 2{,}718||
La fonction logarithmique sous la forme |f(x)=a\log_c(bx)| possède une asymptote verticale à |x=0.| Voici les étapes à suivre pour la tracer.
Tracer l’asymptote verticale à |x=0.|
Déterminer de quel côté est située la courbe par rapport à l’asymptote, grâce au signe de |b.|
Calculer les coordonnées de quelques points appartenant à la courbe.
Placer les points dans un plan cartésien et tracer la courbe.
Lorsqu’on trace la courbe d’une fonction logarithmique, on doit s’approcher de plus en plus de l’asymptote, sans jamais y toucher.
Trace la fonction logarithmique dont la règle est |f(x)=-2\log_{3}\left(-\dfrac{x}{2}\right).|
Tracer l’asymptote verticale à |\boldsymbol{x=0}|
Déterminer de quel côté est située la courbe par rapport à l’asymptote, grâce au signe de |\boldsymbol{b}|
On détermine que |b=-\dfrac{1}{2}.| Puisque c’est une valeur négative, la courbe est située à gauche de l’asymptote.||x<0||
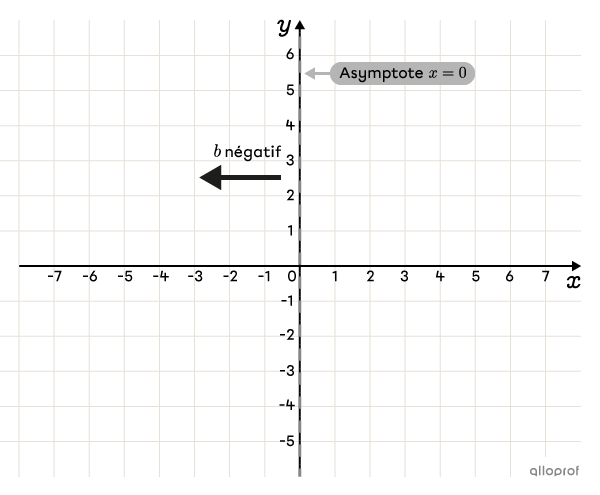
Calculer les coordonnées de quelques points
Comme la courbe est située à gauche de l’asymptote, on doit choisir des valeurs négatives de |x.|
On prend |x=-1.|||\begin{align}f(\color{#FA7921}x)&=-2\log_{3}\left(-\dfrac{\color{#FA7921}x}{2}\right)\\f(\color{#FA7921}{-1})&=-2\log_{3}\left(-\dfrac{\color{#FA7921}{-1}}{2}\right)\\f(-1)&=-2\log_{3}\left(\dfrac{1}{2}\right)\end{align}||On applique maintenant la loi du changement de base afin d’effectuer le calcul.||\begin{align}f(-1)&=-2\left(\dfrac{\log\left(\frac{1}{2}\right)}{\log(3)}\right)\\&\approx -2\left(\dfrac{-0{,}301}{0{,}477}\right)\\&\approx -2(-0{,}63)\\&\approx 1{,}26\end{align}||On a maintenant un premier point appartenant à la fonction : |(-1;1{,}26).| On continue avec une autre valeur de |x.|
On prend |x=-2.| ||\begin{align}f(\color{#FA7921}x)&=-2\log_{3}\left(-\dfrac{\color{#FA7921}x}{2}\right)\\
f(\color{#FA7921}{-2})&=-2\log_{3}\left(-\dfrac{\color{#FA7921}{-2}}{2}\right)\\
f(-2)&=-2\log_{3}(1)
\end{align}||On obtient le logarithme de |1|, ce qui donne |0.|||\begin{align}f(-2)&=-2(0)\\&=0\end{align}||On a maintenant un deuxième point appartenant à la fonction : |(-2,0).|
En continuant de la même manière, on obtient la table de valeurs suivante.
| |x| | |-1| | |-2| | |-4| | |-6| |
|---|---|---|---|---|
| |y| | |1{,}26| | |0| | |-1{,}26| | |-2| |
Placer les points dans un plan cartésien et tracer la courbe
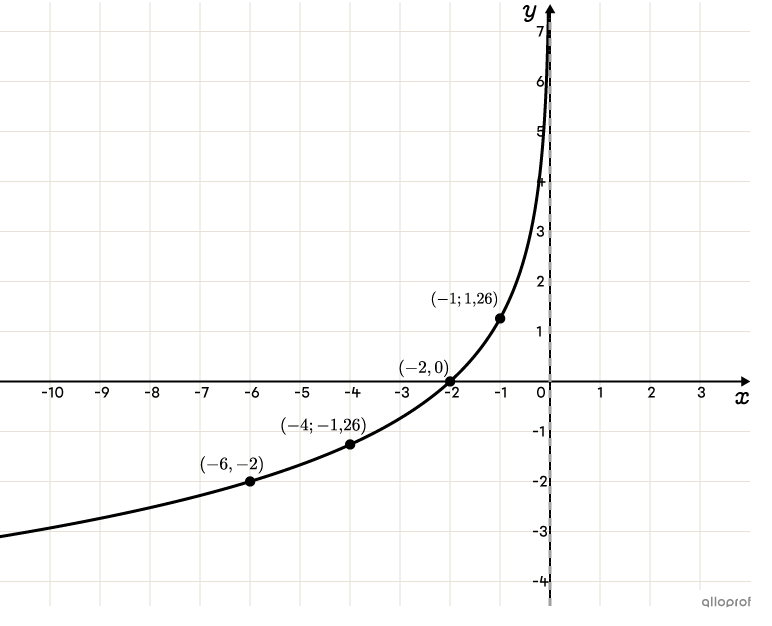
Afin de simplifier les calculs et dans certains cas, d’obtenir des coordonnées entières, on peut choisir des valeurs de |x| de sorte que l’argument du logarithme soit une puissance de la base.
Dans l’exemple précédent, la règle est |f(x)=-2\log_{3}\left(-\dfrac{x}{2}\right).| La base est |\color{#333fb1}3| et l’argument est |\left(\color{#EC0000}{-\dfrac{x}{2}}\right).|
On détermine d’abord les puissances de |\color{#333fb1}3.|||\color{#333fb1}3^\color{#3A9A38}0,\color{#333fb1}3^\color{#3A9A38}1,\color{#333fb1}3^\color{#3A9A38}2,\color{#333fb1}3^\color{#3A9A38}3,\color{#333fb1}3^\color{#3A9A38}4,\dots\\\color{#EC0000}1,\color{#EC0000}3,\color{#EC0000}9,\color{#EC0000}{27},\color{#EC0000}{81},\dots||On trouve ensuite les valeurs de |x| qui permettent d’obtenir ces puissances dans l’argument.
|\begin{align}\color{#ec0000}{-\dfrac{x}{2}}&=\color{#ec0000}1\\
x&=-2\end{align}|
Lorsque |x=-2,| l’argument est |\color{#EC0000}1.|
||\log_{\color{#333fb1}3}(\color{#EC0000}{1})\\
\Downarrow\\
\color{#3A9A38}{0}||
|\begin{align}\color{#ec0000}{-\dfrac{x}{2}}&=\color{#ec0000}3\\
x&=-6\end{align}|
Lorsque |x=-6,| l’argument est |\color{#EC0000}3.|
||\log_{\color{#333fb1}3}(\color{#EC0000}{3})\\
\Downarrow\\
\color{#3A9A38}{1}||
|\begin{align}\color{#ec0000}{-\dfrac{x}{2}}&=\color{#ec0000}9\\
x&=-18\end{align}|
Lorsque |x=-18,| l’argument est |\color{#EC0000}9.|
||\log_{\color{#333fb1}3}(\color{#EC0000}{9})\\
\Downarrow\\
\color{#3A9A38}{2}||
Ainsi, en choisissant |x=-2,| |x=-6| et |x=-18,| il n’est pas nécessaire de faire un changement de base pour effectuer la suite du calcul. De plus, les réponses obtenues sont entières.
Pour tracer une fonction logarithmique sous la forme |f(x)=a\log_c\big(b(x-h)\big)+k,| les étapes sont les mêmes que sous la forme |f(x)=a\log_c(bx),| sauf que l’équation de l’asymptote est |x=h.|
Tracer l’asymptote verticale à |x=h.|
Déterminer de quel côté est située la courbe par rapport à l’asymptote, grâce au signe de |b.|
Calculer les coordonnées de quelques points appartenant à la courbe.
Placer les points dans un plan cartésien et tracer la courbe.
Trace la fonction logarithmique dont la règle est |f(x)=-\log_{2}(x+3)-4.|
Tracer l’asymptote verticale à |\boldsymbol{x=h}|
Puisque |h=-3,| l’équation de l’asymptote est |x=-3.|
Déterminer de quel côté est située la courbe par rapport à l’asymptote, grâce au signe de |\boldsymbol{b}|
On détermine que |b=1.| Puisque c’est une valeur positive, la courbe est située à droite de l’asymptote.||x>-3||
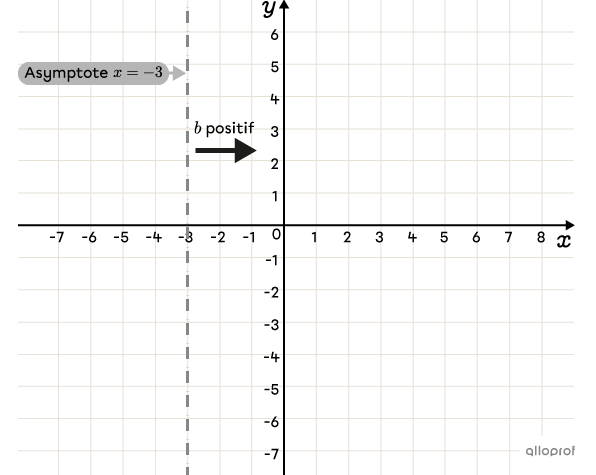
Calculer les coordonnées de quelques points
On doit choisir des valeurs de |x| supérieures à |-3.|
On prend |x=-2.|||\begin{align}f(\color{#FA7921}x)&=-\log_{2}(\color{#FA7921}x+3)-4\\f(\color{#FA7921}{-2})&=-\log_{2}(\color{#FA7921}{-2}+3)-4\\f(-2)&=-\log_{2}(1)-4\end{align}||On obtient le logarithme de |1|, ce qui donne |0.|||\begin{align}f(-2)&=-(0)-4\\&=-4\end{align}||On a maintenant un premier point appartenant à la fonction : |(-2,-4).| On continue avec une autre valeur de |x.|
On prend |x=-1.|||\begin{align}f(\color{#FA7921}x)&=-\log_{2}(\color{#FA7921}x+3)-4\\f(\color{#FA7921}{-1})&=-\log_{2}(\color{#FA7921}{-1}+3)-4\\f(-1)&=-\log_{2}(2)-4\\f(-1)&=-(1)-4\\f(-1)&=-5\end{align}||On a maintenant un deuxième point appartenant à la fonction : |(-1,-5).| On peut s’intéresser au calcul de l’ordonnée à l’origine.
On prend |x=0.|||\begin{align}f(\color{#FA7921}x)&=-\log_{2}(\color{#FA7921}x+3)-4\\
f(\color{#FA7921}{0})&=-\log_{2}(\color{#FA7921}{0}+3)-4\\
f(0)&=-\log_{2}(3)-4\end{align}||On applique maintenant la loi du changement de base afin d’effectuer le calcul.
||\begin{align}f(0)&=-\left(\dfrac{\log3}{\log2}\right)-4\\&\approx -(1{,}58)-4\\&\approx -5{,}58\end{align}||L’ordonnée à l’origine est donc de |-5{,}58.|
En utilisant l’astuce mentionnée plus haut, on obtient la table de valeurs suivante.
| |x| | |-2| | |-1| | |0| | |1| | |5| |
|---|---|---|---|---|---|
| |y| | |-4| | |-5| | |-5{,}58| | |-6| | |-7| |
Placer les points dans un plan cartésien et tracer la courbe


Moments dans la vidéo :