Matières
Niveaux
Les calculs dans les circuits électriques
Fiche | Sciences et technologies
Secondaire
4
Table des matières
Lorsque vient le temps d'identifier une valeur d'intensité, de tension ou de résistance dans un circuit électrique, il faut tout d'abord identifier le type de circuit (en série ou en parallèle) afin de savoir quelles lois peuvent être utilisées dans le problème. Les lois de Kirchhoff et les formules sur la résistance équivalente permettent d'établir des relations selon le type de circuit. De plus, la loi d'Ohm permet également de faire des liens entre les trois paramètres étudiés dans un circuit électrique.
Formules à utiliser dans les circuits électriques
| Circuit en série |
Circuit en parallèle
|
|
| Tension |\left(\text{V}\right)| | |U_{t} \space \text {ou} \space U_{s} = U_{1} + U_{2} + U_{3} + ...| | |U_{t} \space \text {ou} \space U_{s} = U_{1} = U_{2} = U_{3} = ...| |
| Intensité du courant |\left(\text{A}\right)| | |I_{t} \space \text {ou} \space I_{s} = I_{1} = I_{2} = I_{3} = ...| | |I_{t} \space \text {ou} \space I_{s} = I_{1} + I_{2} + I_{3} + ...| |
|
Résistance |\left(\Omega\right)|
|
|R_{eq} = R_{1} + R_{2} + R_{3} + ...| | |\displaystyle \frac {1}{R_{eq}} = \frac {1}{R_{1}} + \frac {1}{R_{2}} + \frac {1}{R_{3}} + ...| |
Quelle est la résistance du résistor |R_{2}|?
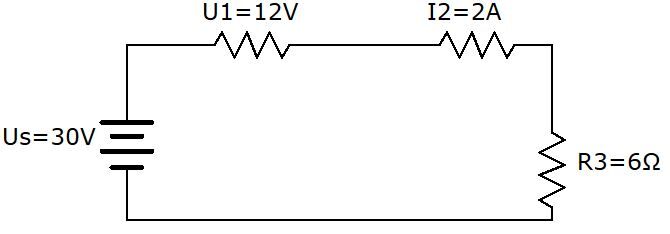
Il est préférable de compléter un tableau afin de bien cerner les données connues dans le problème.
| Tension | Résistance | Intensité |
|---|---|---|
| |U_{s} = 30 \text { V}| | |R_{eq} = | | |I_{s} = | |
| |U_{1} = 12 \text { V}| | |R_{1} = | | |I_{1} = | |
| |U_{2} = | | |R_{2} = | | |I_{2} = 2 \text{ A}| |
| |U_{3} = | | |R_{3}=6 \: \Omega| | |I_{3} =| |
Puisque le circuit est en série, la loi des noeuds permet de déduire que l'intensité du courant sera toujours la même.
| Tension | Résistance | Intensité |
|---|---|---|
| |U_{s} = 30 \: \text {V}| | |R_{eq} = | | |I_{s} = \color{red}{2 \: \text{A}}| |
| |U_{1} = 12 \: \text {V}| | |R_{1} = | | |I_{1} = \color{red}{2 \: \text{A}}| |
| |U_{2} = | | |R_{2} = | | |I_{2} = 2 \: \text{A}| |
| |U_{3} = | | |R_{3}=6 \: \Omega| | |I_{3} = \color{red}{2 \: \text{A}}| |
En utilisant la loi d'Ohm, il est possible de déterminer la tension circulant dans la troisième résistance.
||\begin{align} U_{3}= R_{3} \times I_{3} \quad \Rightarrow \quad U_{3}&= 6\ \Omega \times 2\ \text{ A} \\ &= 12 \text{ V} \end{align} ||| Tension | Résistance | Intensité |
|---|---|---|
| |U_{s} = 30 \: \text {V}| | |R_{eq} = | | |I_{s} = 2 \: \text{A}| |
| |U_{1} = 12 \: \text {V}| | |R_{1} = | | |I_{1} = 2 \: \text{A}| |
| |U_{2} = | | |R_{2} = | | |I_{2} = 2 \: \text{A}| |
| |U_{3} = \color{red}{12 \: \text {V}} | | |R_{3}=6 \: \Omega| | |I_{3} = 2 \: \text{A}| |
La loi des boucles permet ensuite de déduire la tension dans le deuxième résistor.
||\begin{align} U_{s}= U_{1} + U_{2} + U_{3} \quad \Rightarrow \quad U_{2}&= U_{s}- U_{1} - U_{3} \\ &= 30 \text{ V} - 12 \text{ V} - 12 \text{ V} \\ &= 6 \: \text {V}\end{align}||| Tension | Résistance | Intensité |
|---|---|---|
| |U_{s} = 30 \: \text {V}| | |R_{eq} = | | |I_{s} = 2 \: \text{A}| |
| |U_{1} = 12 \: \text {V}| | |R_{1} = | | |I_{1} = 2 \: \text{A}| |
| |U_{2} = \color{red}{6 \: \text {V}} | | |R_{2} = | | |I_{2} = 2 \: \text{A}| |
| |U_{3} = 12 \: \text {V} | | |R_{3}=6 \: \Omega| | |I_{3} = 2 \: \text{A}| |
Finalement, la résistance |R_{2}| peut être déterminée à partir de la loi d'Ohm.
||\begin{align} U_{2}= R_{2} \times I_{2} \quad \Rightarrow \quad R_{2}&= \frac{U_{2}}{I_{2}} \\ &= \frac{6 \text{ V}}{2 \text{ A}} \\ &= 3\ \Omega \end{align} || Le résistor |R_2| a une résistance de |3\ \Omega|.
Quelle est la résistance équivalente de ce circuit?
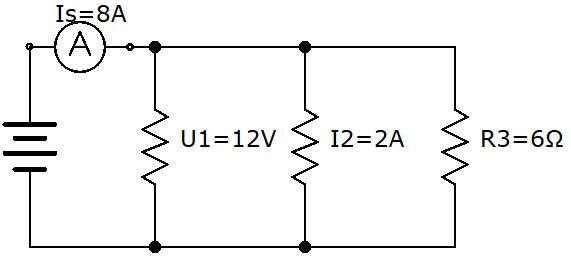
Tout comme l'exemple précédent, il est préférable de compléter un tableau afin de bien cerner les données connues dans le problème.
| Tension | Résistance | Intensité |
|---|---|---|
| |U_{s} = | | |R_{eq} = | | |I_{s} = 8 \: \text{A}| |
| |U_{1} = 12 \: \text {V}| | |R_{1} = | | |I_{1} = | |
| |U_{2} = | | |R_{2} = | | |I_{2} = 2 \: \text{A}| |
| |U_{3} = | | |R_{3}=6 \: \Omega| | |I_{3} =| |
Puisque le circuit est en parallèle, la loi des boucles permet de déduire que la tension sera toujours la même.
| Tension | Résistance | Intensité |
|---|---|---|
| |U_{s} = \color{red}{12 \: \text {V}}| | |R_{eq} = | | |I_{s} = 8 \: \text{A}| |
| |U_{1} = 12 \: \text {V}| | |R_{1} = | | |I_{1} = | |
| |U_{2} =\color{red}{12 \: \text {V}} | | |R_{2} = | | |I_{2} = 2 \: \text{A}| |
| |U_{3} =\color{red}{12 \: \text {V}} | | |R_{3}=6 \: \Omega| | |I_{3} =| |
En utilisant la loi d'Ohm, il est possible de déterminer l'intensité du courant circulant dans la troisième résistance.
||\begin{align} U_{3}= R_{3} \times I_{3} \quad \Rightarrow \quad I_{3}&= \frac{U_{3}}{R_{3}} \\ &= \frac{12 \text{ V}}{6 \ \Omega} \\ &= 2 \text{ A} \end{align}||| Tension | Résistance | Intensité |
|---|---|---|
| |U_{s} = 12 \: \text {V}| | |R_{eq} = | | |I_{s} = 8 \: \text{A}| |
| |U_{1} = 12 \: \text {V}| | |R_{1} = | | |I_{1} = | |
| |U_{2} = 12 \: \text {V}| | |R_{2} = | | |I_{2} = 2 \: \text{A}| |
| |U_{3} =12 \: \text {V}| | |R_{3}=6 \: \Omega| | |I_{3} =\color {red}{2 \: \text{A}}| |
La loi des noeuds permet ensuite de déduire l'intensité dans le deuxième résistor.
||\begin{align} I_{s} = I_{1} + I_{2} + I_{3} \quad \Rightarrow \quad I_{2}&= I_{s} - I_{1} - I_{3} \\ &= {8 \text{ A}}-{2 \ \text{ A} - 2\text{ A}} \\ &= 4 \text{ A} \end{align} ||| Tension | Résistance | Intensité |
|---|---|---|
| |U_{s} = 12 \: \text {V}| | |R_{eq} = | | |I_{s} = 8 \: \text{A}| |
| |U_{1} = 12 \: \text {V}| | |R_{1} = | | |I_{1} = \color {red}{4 \: \text{A}}| |
| |U_{2} = 12 \: \text {V}| | |R_{2} = | | |I_{2} = 2 \: \text{A}| |
| |U_{3} =12 \: \text {V}| | |R_{3}=6 \: \Omega| | |I_{3} = 2 \: \text{A}| |
Les valeurs de résistance des résistors |R_{1}| et |R_{2}| peuvent être déterminées à partir de la loi d'Ohm. ||\begin{align} U_{1}= R_{1} \times I_{1} \quad \Rightarrow \quad R_{1}&= \frac{U_{1}}{I_{1}} & U_{2}= R_{2} \times I_{2} \quad \Rightarrow \quad R_{2}&= \frac{U_{2}}{I_{2}} \\ &= \frac{12 \text{ V}}{4 \text{ A}} &&= \frac{12 \text{ V}}{2 \text{ A}} \\ &= 3\ \Omega& &= 6\ \Omega \end{align} ||
| Tension | Résistance | Intensité |
|---|---|---|
| |U_{s} = 12 \: \text {V}| | |R_{eq} = | | |I_{s} = 8 \: \text{A}| |
| |U_{1} = 12 \: \text {V}| | |R_{1} = \color {red}{3 \: \Omega}| | |I_{1} = 4 \: \text{A}| |
| |U_{2} = 12 \: \text {V}| | |R_{2} = \color {red}{6 \: \Omega}| | |I_{2} = 2 \: \text{A}| |
| |U_{3} =12 \: \text {V}| | |R_{3}=6 \: \Omega| | |I_{3} = 2 \: \text{A}| |
Finalement, la résistance équivalente du circuit peut être calculée.
||\begin{align} \frac{1}{R_{eq}}= \frac{1}{R_{1}}+\frac{1}{R_{2}}+\frac{1}{R_{3}} \quad \Rightarrow \quad \frac{1}{R_{eq}} &= \frac{1}{3 \: \Omega}+\frac{1}{6 \: \Omega}+\frac{1}{6 \: \Omega} \\ \frac{1}{R_{eq}} &= \frac{4}{6 \: \Omega} \\ R_{eq} &= 1,5 \:\Omega \end{align}||Le même résultat peut être déterminé avec la loi d'Ohm.
||\begin{align} U_{s}= R_{eq} \times I_{s} \quad \Rightarrow \quad R_{eq}&= \frac{U_{s}}{I_{s}} \\ &= \frac{12 \text{ V}}{8 \text{ A}} \\ &= 1,5\ \Omega \end{align} || La résistance équivalente de ce circuit est |1,5\ \Omega|.
Pour valider ta compréhension à propos des calculs dans les circuits électriques de façon interactive, consulte la MiniRécup suivante :
Vidéo
