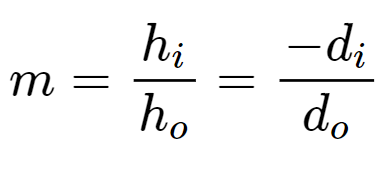Best Of
Re: Question
Salut!
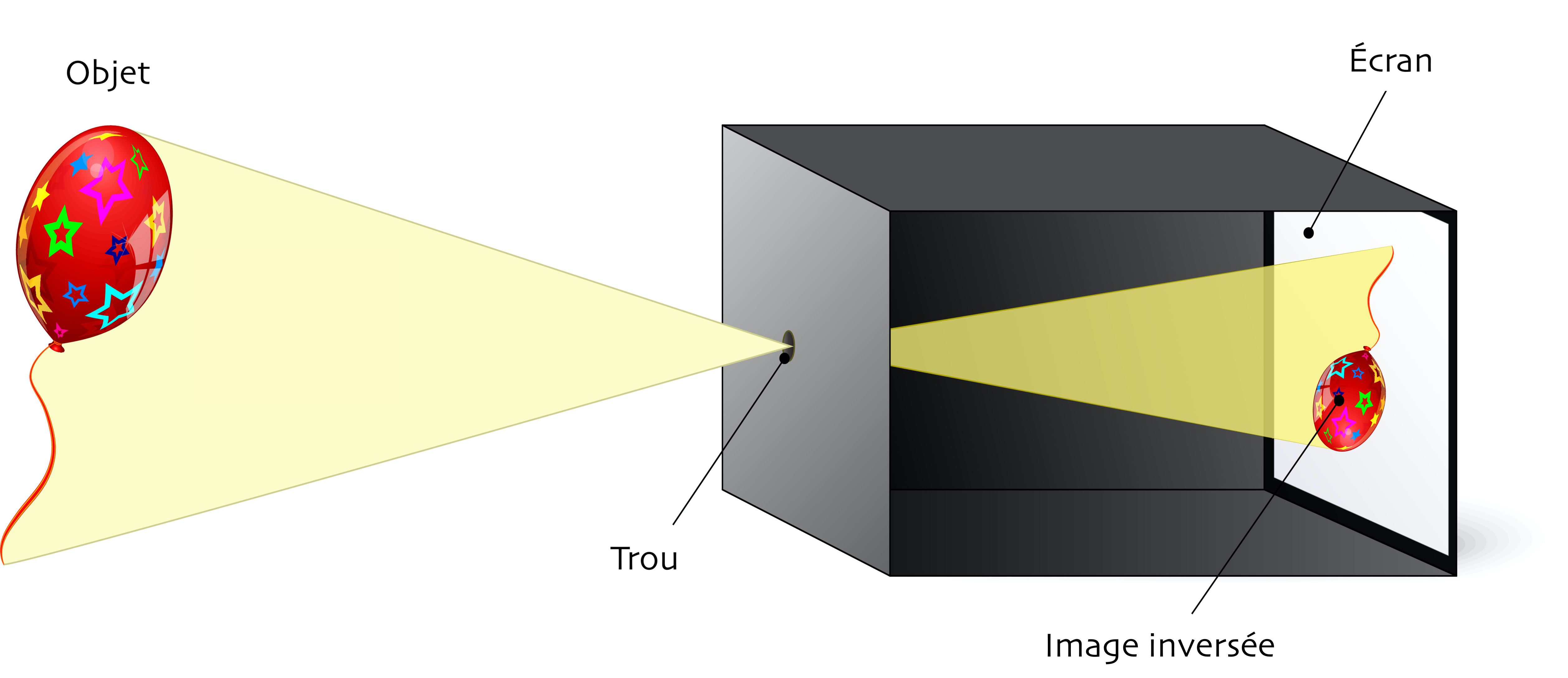
Les rayons convergent pour former une image réelle inversée du côté opposé de la lentille par rapport à l'objet.
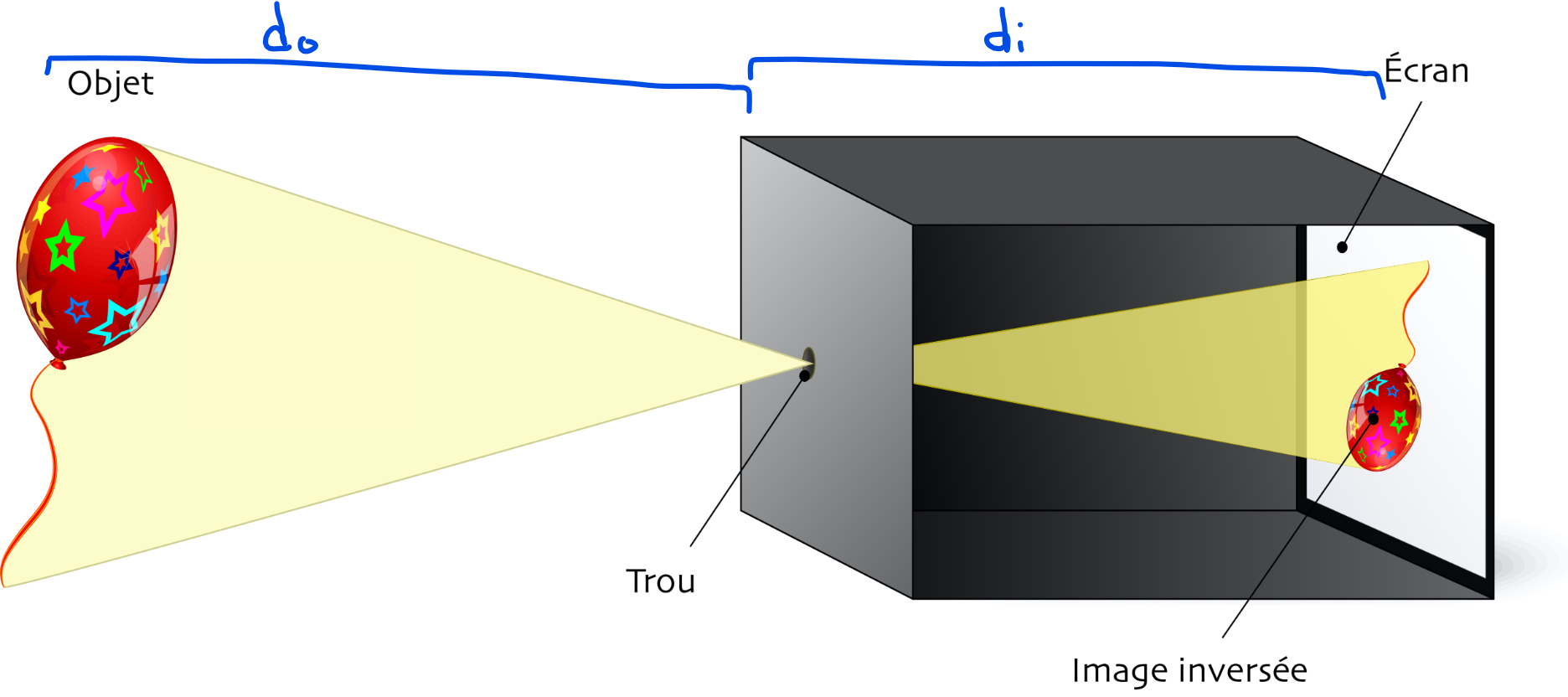
On nous dit que la distance entre l'objet et son image est de 20 cm. On a donc l'équation :
$$ d_{o}+d_{i} = 20$$
On cherche la distance qui sépare l'image du sténopé, donc \(d_{i}\)
On sait aussi que l'image est 4 fois plus petite que l'objet :
$$h_{i}=\frac{h_{o}}{4}$$
ou
$$4h_{i}=h_{o}$$
On peut transformer cette équation pour trouver le grandissement m = \(\frac{h_{i} }{h_{o}}\) :
$$4=\frac{h_{o}}{h_{i}}$$
$$\frac{1}{4}=\frac{h_{i}}{h_{o}}$$
Puis, on peut utiliser la formule de grandissement faisant intervenir \(d_{i}\) et \(d_{o}\) :
et l'équation :
$$ d_{o}+d_{i} = 20$$
pour trouver \(d_{i}\).
Je te laisse essayer avec ces indices. Tu peux retrouver toutes les formules utiles à utiliser lorsqu'on travaille avec des lentilles juste ici : Les équations des lentilles | Alloprof
J'espère que cela t'aide! :)
Re: Question
Salut !
Allons-y une question à la fois. Cependant, voici une fiche qui contient des détails intéressants.
Le modèle de Thomson explique les phénomènes électriques en supposant que les électrons sont les porteurs de charges négatives à l'intérieur de l'atome.
La feuille d'or a été choisie parce qu'elle est extrêmement fine et peut laisser passer les particules.
Bohr a proposé que les électrons ne perdent pas d'énergie lorsqu'ils sont sur des orbites quantifiées spécifiques autour du noyau. C'est cet orbite qui permet aux électrons de ne pas s'écraser sur les protons, un peu comme la Lune autour de la Terre.
Les particules élémentaires sont l'électron, le proton et le neutron.
J'espère que cela ait pu t'aider et si tu as d'autres questions, n'hésite pas !
Bonne journée !
Re: Question
Bonjour! :)
Nous sommes désolés pour cela. Il y a en effet un petit problème technique. Notre équipe travaille fort pour le régler! :)
Si tu le souhaites, tu peux signaler le bogue en remplissant le formulaire suivant: https://alloprof-ti.atlassian.net/servicedesk/customer/portal/6/group/13
Merci beaucoup pour ta collaboration! À la prochaine! :)
Sarah G
Question
Bonjour! En commencent j'aimerais vous dire que votre site internet m'a énormément aidez quand j'étais a l'école. J'étais toujours rendu sur le site xD l'école n'était pas assez rapide pour ma soif d'apprentissage. Et cela fait bien une dizaine d'année depuis le secondaire! Je suis quelqu'un d'un peu perfectionniste et nostalgique. J'aimerais bien savoir ou il est possible d'avoir d'anciens examen du ministère autant au primaire qu'au secondaire. Je regarde sur google mais je ne trouve rien... Pourtant je lis qu'après 3 ans les examens peuvent être utilisé? Je rêve depuis longtemps de les refaire! Merci:)
Re: Question
Salut !
J'imagine que tes réponses sont correct, mais je te conseille d'utiliser des fractions dans tes calculs et réponse pour être plus exact.
Par exemple, pour le b), tu dois multiplier les fractions ensembles.
$$ (2^{\frac{1}{2}})^{\frac{1}{6}}=2^{\frac{1}{2}\times\frac{1}{6}} $$
J'espère que cela ait pu t'aider et si tu as d'autres questions, n'hésite pas !
Bonne journée !
Re: Question
C'est bien la bonne réponse
h(x) = f(x)/g(x) pour g(x) ≠ 0 donc pour x ≠ -1
h(x) = (x² - 2x - 3)/(x + 1) = (x - 3)(x + 1)/(x + 1) = x - 3
Si y = h(x) = x - 3 pour x ≠ -1 => y peut prendre toutes les valeurs réelles sauf y = (-1) -3 = -4
Re: Question
Salut !
La composition de fonctions est une opération consistant à remplacer la variable indépendante de la première fonction par l'expression représentant la variable dépendante de la seconde fonction.
La fonction g est polynomial de degré 1 (\(y=ax+b\)). Cela te donne une fonction suivante :
$$ g(f(x))=g(3x+5)=a(3x+5)+b=3ax+5a+b $$
$$ 3ax+5a+b=x+1 $$
Je te laisse continuer par toi-même à partir de là. J'espère que cela ait pu t'aider et si tu as d'autres questions, n'hésite pas !
Bonne journée !
Re: Question
Salut !
Il s'agit du même principe, tu connais la valeur \(x\) qui ne fait pas parti du domaine \(x=-1\). Tu dois donc trouver la valeur de \(h(-1)\).
J'espère que cela ait pu t'aider et si tu as d'autres questions, n'hésite pas !
Bonne journée !
Re: Question
Salut !
Merci de faire appel au service d'Alloprof ! Il me semble que tu as eu un problème au niveau de la racine carré.
Une racine peut s'écrire sous la forme d'un exposant fractionnaire.
$$ \sqrt{x}=(x)^{\frac{1}{2}} $$
Ainsi, tu dois diviser par deux ton exposant à la -14.
J'espère que cela ait pu t'aider et si tu as d'autres questions, n'hésite pas !
Bonne journée !
Re: Question
Bonjour ElfeTimide5414,
Merci pour ta question :)
Tu as bien commencé en trouvant la première restriction, c'est-à-dire celle où le dénominateur ne peut être égal à zéro (donc x ne peut être égal à -1 et 2). La seconde restriction provient de la racine carrée. En effet, l'expression à l'intérieur ne peut être négative si on veut qu'elle fasse partie du domaine des réels.
Tu as aussi commencé les bons calculs lorsque tu as fait x+3>=0 et x ^2-x-2>0. Ça nous permet de voir lorsque chacune des fonctions fonction est positive. On peut donc voir que x+3 est positive lorsqu'elle est plus grande ou égale à -3. Pour le dénominateur, on peut calculer que la fonction est négative entre -1 et 2. Donc entre -1 et 2, le numérateur serait positif, mais le dénominateur serait négatif. Le résultat serait donc un négatif dans une racine carrée, ce qui est impossible.
J'espère que cela répond à ta question :)
Sandrine