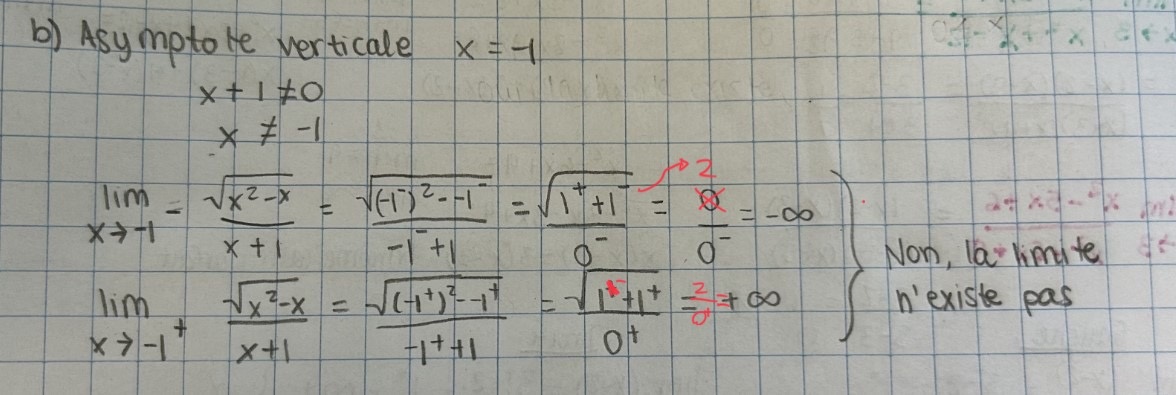Best Of
Question
Bonjour! Les ondes sonores sont-elles longitudinales ou transversale? Merci!
Question
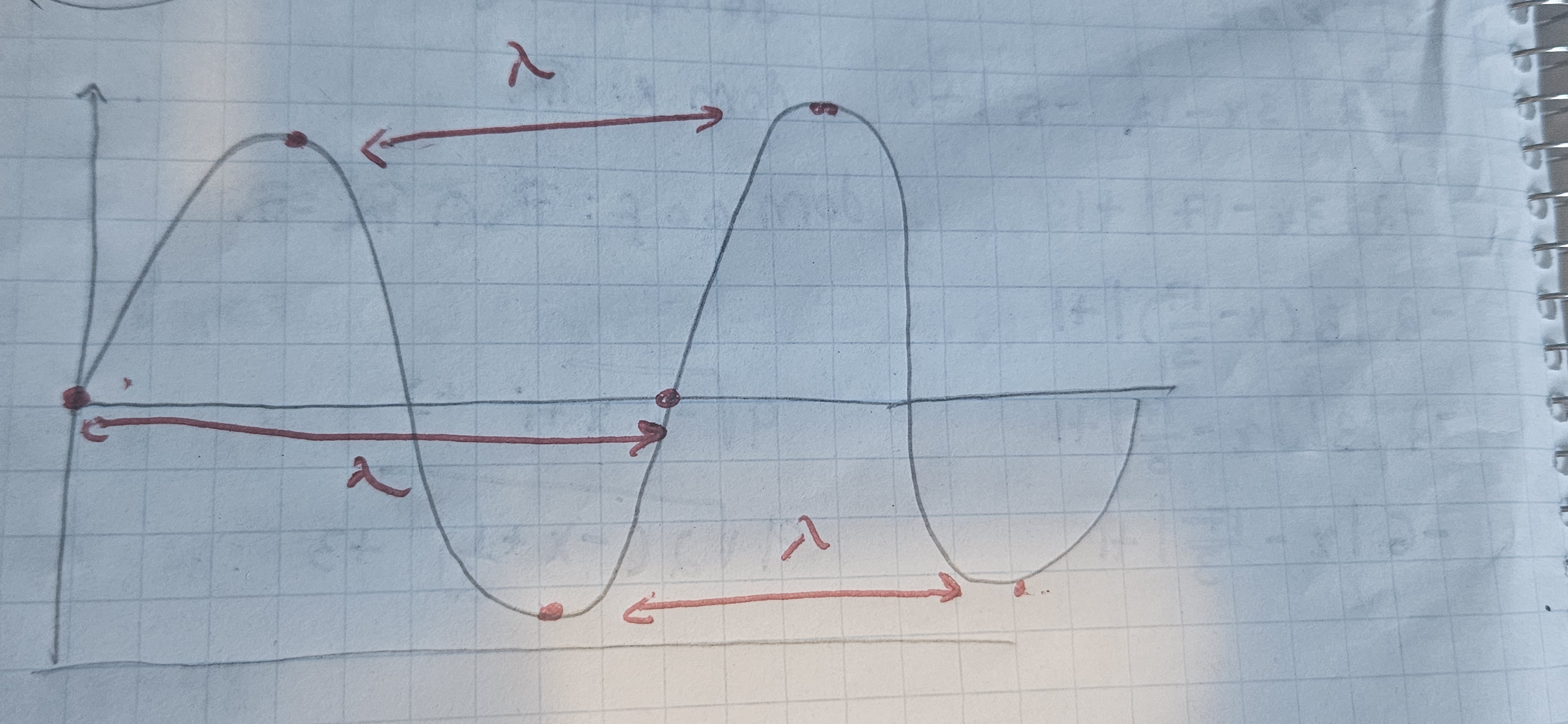
Bonjour! Je ne suis pas sûre de comprendre la notion d'un cycle dans une onde. Si on dit que λ est la distance entre deux points séparés par un cycle, laquelle ici est correct? Sont-ils tous correct? C'est quoi un cycle? Merci!!
Question
Bonjour! Je ne comprends pas ce problème, pourriez-vous m'aider s'il vous plaît? Merci!
Lors de certains orages, on voit un éclair et, après un certain laps de temps, on entend le tonnerre. Ces deux phénomènes ondulatoires se produisent simultanément, mais sont perçus avec un décalage dans le temps. Cela s'explique par la différence de leurs vitesses de propagation. Le son du tonnerre a une vitesse de propagation d'environ 330 m/s; on l'entend avec un retard temporel, tandis qu'on perçoit instantanément la lumière de l'éclair (c = 3,00 x10^8 m/s). En tenant compte de ces renseignements, calculez la distance (d) à laquelle s'est produit l'éclair si on entend le tonnerre avec quatre secondes de retard.
Question
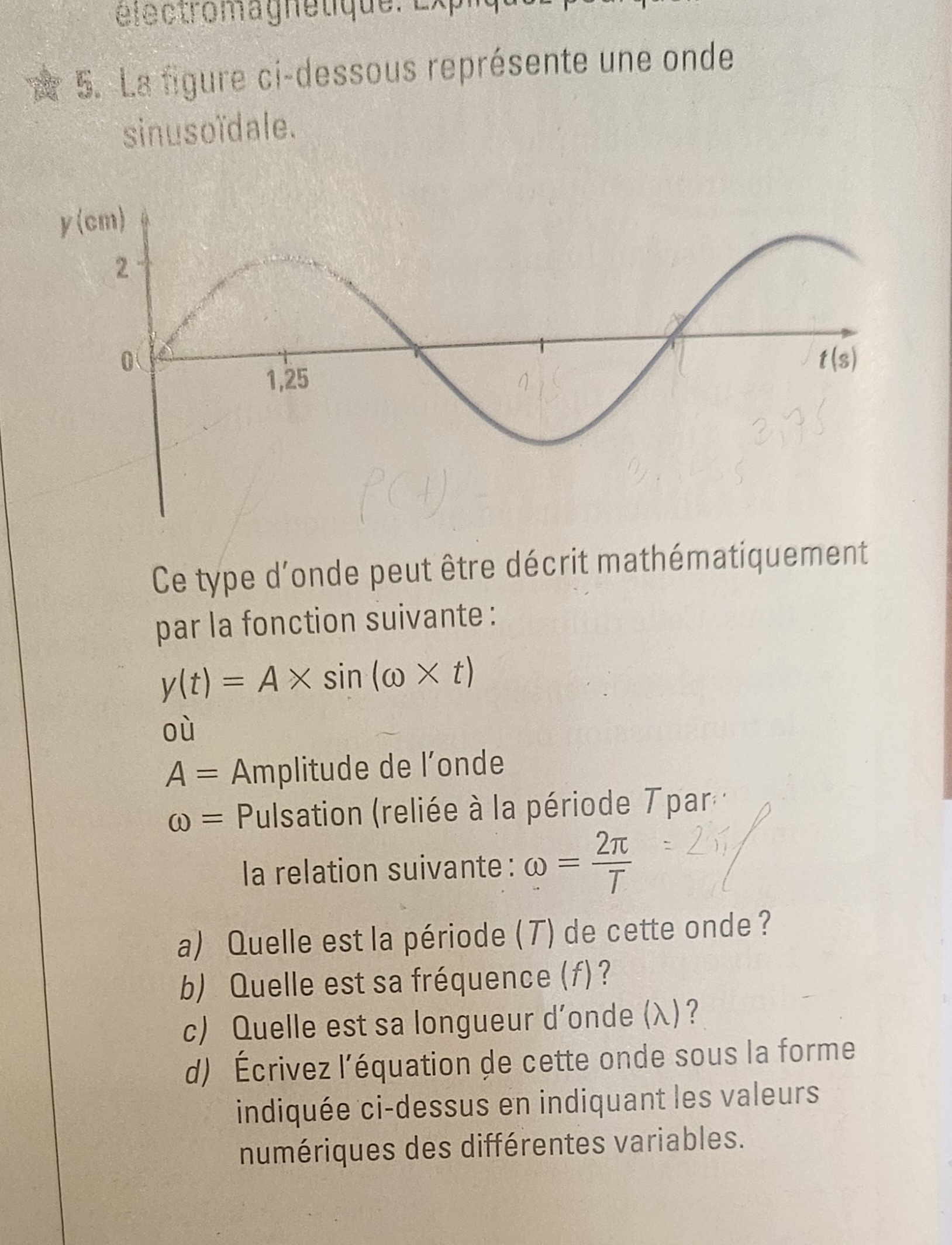
Bonjour! Je suis bloquée sur ce problème. Nous n'avons pas encore travailler la fct sinus en math SN5, donc je ne sais pas comment résoudre les problème ci-dessous... Pourriez vous m'aider? Merci!
Question
Bonsoir, je travaille sur un rapport de labo sur la deuxième loi de la réflexion, cependant, c'est la première fois dans un rapport que nous rentrons la notion d'erreur absolue, alors j'ai un peu de misière sur comment faire mon analyse.
Ainsi, comment puis-je élaborer que, par exemple, lors de l'expérience, le premier angle d'incidence (10 degres) n'est pas égal à l'angle de réflexion (11 degres)? Pourrais-je avoir une piste? Merci beaucoup!
Question
Bonsoir! C'est par rapport au laser utilisé lors de l'expérience. On l'a pointé sur le miroir pour obtenir l'angle de réflexion. Le problème, C'est que le rayon du laser est très large. Il couvre plusieures données a la fois donc j'aimerai savoir si il faut lui attribuer une incertitude?
Re: Question
Pour ton calcul b, la réponse finale est bonne, il y a juste deux petites erreurs (en rouge) dans la démarche:
Re: Question
Salut,
En regardant ça, il doit y avoir une erreur dans le corrigé, car je ne vois pas comment -1 pourrait être inclu dans le domaine(h).
Pour ce qui est des asymptotes horizontales, c'est pas la chose la plus facile quand on travaille avec des racines, mais je vais te montrer ma démarche:
En bref, transforme tes racines le plus possible et n'oublie pas les valeurs absolues lorsque tu sors un x^2 de la racine.
Re: Question
Bonjour !
Sans Calculatrice, tu peux estimer la racine carrée en trouvant les carrés parfaits les plus proches de ce nombre. Par exemple, pour trouver la racine carrée de 20:
- on sait que 16 et 25 sont les carrés parfaits les plus proches, ce qui signifie que la racine carrée de 20 se situe entre 4 et 5. On peut donc obtenir une approximation de la racine carrée.
J'espère que cela t'auras été utile.
Bonne journée :)
Re: Question
Bonjour,
Pour exprimer 6.42 × 10^9 sous forme décimale, il suffit de déplacer la virgule vers la droite de 9 places, car l'exposant est positif.
Lorsque l'exposant est positif (comme dans 10^9), cela signifie que le nombre est multiplié par 10 plusieurs fois (ici 9 fois). Chaque multiplication par 10 augmente la valeur du nombre en déplaçant la virgule vers la droite et en ajoutant des zéros à la droite.
Si l'exposant est négatif, on déplacerait la virgule vers la gauche et on ajouterait des zéros à gauche aussi.
Exemple :
Pour 3.5 × 10^(-3), on déplace la virgule de 3.5 vers la gauche de 3 places. Cela donne 0.0035, ce qui représente un nombre plus petit.
Pour 3.5 × 10^(3), on déplace la virgule de 3.5 vers la droite de 3 places. Cela donne 3500, ce qui représente un nombre plus grand.
N'hésite pas si tu as encore des questions !
Bonne journée :)