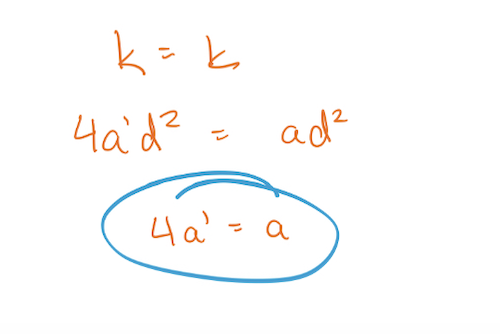Best Of
Re: Question
Salut !
Si tu n'es pas sûr, tu peux visiter cette fiche.
La liste des concepts sujets à évaluation présentée dans cette fiche représente tous les concepts prescrits susceptibles d'être évalués en science et technologie (ST).
Tu peux aussi comparer les deux listes. J'espère que cela ait pu t'aider et si tu as d'autres questions, n'hésite pas !
Bonne journée !
Re: Question
Salut !
Le premier jour des règles est le jour 1 du cycle et le dernier jour du cycle est le jour avant le début des prochaines règles.
Aussi, la menstruation vient en effet de l'endomètre. J'espère que cela ait pu t'aider et si tu as d'autres questions, n'hésite pas !
Bonne journée !
Re: Question
Salut RubisKappa8548!
Merci pour ta question. :)
Pour ce qui est du développement de cette expression algébrique, tu dois commencer en respectant la priorité des opérations.
Ta première étape sera donc de t'occuper des exposants. Ainsi, le binôme (3x - 1) est au carré. Tu devras donc le multiplier par lui-même :
- (3x - 1) * (3x - 1)
Lorsque tu multiplies des termes entre parenthèses, tu dois toujours procéder de la même façon, soit :
- Multiplier le 1er terme de la 1ère parenthèse avec le 1er terme de la 2e parenthèse ;
- Multiplier le 1er terme de la 1ère parenthèse avec le 2e terme de la 2e parenthèse ;
- Multiplier le 2e terme de la 1ère parenthèse avec le 1er terme de la 2e parenthèse ;
- Multiplier le 2e terme de la 1ère parenthèse avec le 2e terme de la 2e parenthèse.
Tu obtiendras alors un trinôme. Tu pourras multiplier le binôme entre parenthèse restant (x + 2) avec ce trinôme en empruntant la même démarche que pour l'étape 1, ce qui te permettra d'obtenir le polynôme du c).
Au besoin, je t'invite à consulter cette fiche pour te remémorer les informations importantes à connaître lors de ce type de résolution!
En espérant que cela répond à ta question. Si tu en as d'autres, n'hésite surtout pas à nous réécrire, il nous fera plaisir de t'aider à nouveau!
À bientôt,
Océane :)
Re: Question
Salut !
Je suppose que cette partie de la démarche est le calcul de l'aire du rectangle. Si tu prend la distance LG, tu obtiens la plus grande valeur moins la plus petite \(24-y\).
J'espère que cela ait pu t'aider et si tu as d'autres questions, n'hésite pas !
Bonne journée !
Re: Question
Bonjour!
Pour répondre à cette question, tu dois commencer par multiplier le nombre de kilomètre qu'a parcouru Molly par 2. En effet, on indique que Natalia en a fait le double, ce qui signifie que nous devons multiplier par deux.
Ensuite, on indique qu'on doit trouver la distance parcourue en tout. Comme on parle du total de kilomètre parcouru par les deux amies, on devra... Je te laisse compléter :)
Le x fois plus indique donc le nombre par lequel tu devras multiplier l'autre nombre. Si on dit que Natalia a fait 1 fois plus de kilomètres, alors tu devras multiplier le nombre de kilomètres de Molly par 1! :)
J'espère t'avoir aidé!
Si tu as d'autres questions, n'hésite pas à nous réécrire. Nous te répondrons avec plaisir!
Laurie :)
Re: Question
Bonjour!
Le fascisme est une idéologie contraire au communisme. Avec la montée du communisme, le fascisme monte en réaction afin de le contrer. C'est ainsi que, par exemple, Adolf Hitler a réussi à s'emparer du pouvoir. C'est en s'alliant avec le parti conservateur (un autre parti contre le communisme), qu'Hitler arrive à devenir chancelier d'Allemagne. Le parti nazi s'opposait à la démocratie, l'individualisme, au capitalisme, à la liberté économique, au parlementarisme, au communisme et au socialisme.
Je te suggère de consulter la fiche ci-dessous pour en savoir plus sur le fascisme :
Si tu as d'autres questions, n'hésite pas à nous réécrire. Nous te répondrons avec plaisir!
Laurie :)
Re: Question
Salut OrSage221!
Merci pour ta question. :)
Notre document préparatoire regroupe effectivement toutes les notions à l'étude en vue de cet examen! Toutefois, si tu souhaites obtenir davantage d'informations quant à la préparation, je t'invite à consulter cette fiche!
En espérant que cela répond à ta question. Si tu en as d'autres, n'hésite surtout pas à nous réécrire, il nous fera plaisir de t'aider à nouveau!
À bientôt,
Océane :)
Re: Question
Salut !
L'exercice s'effectue en deux étapes. La première est de trouver la règle de la fonction \(f(x)\) à l'aide des informations du graphique.
$$ f(x)=a(x-h)^2+k $$
Il est possible de trouver la valeurs des zéros à l'aide de cette règle.
La deuxième partie consiste à trouver la règle de la deuxième fonction. Le sommet reste le même, mais tu dois trouver la nouvelle valeur des zéros en doublant la distance entre les deux.
J'espère que cela ait pu t'aider et si tu as d'autres questions, n'hésite pas !
Bonne journée !
Re: Question
Salut :D
Voici ma démarche, mais je te conseille de seulement regarder le début (la 1re image) et essayer de faire le reste par toi-même.
Si mon écriture ne te semble pas compréhensible (ce qui est très possible), dis-toi que je suis toujours ouverte à apporter plus de clarifications.
Ne lâche pas
Bonne journée :)
Re: Question
Bonjour! :) Merci d'utiliser la Zone d'Entraide!
La neutralisation se caractérise par la réaction de deux réactifs (une base et un acide) qui a pour produits de l'eau et un sel.
Généralement, l'équation prend la forme suivante:
- Acide+Base → Sel+Eau
Voyons ensemble les exemples suivants:
- Dans le premier cas, on voit l'acide (HCl) avec la base NaOH. ***On reconnait la base par sa forme OH.
- Dans le deuxième cas, l'acide est le H2SO4 et la base est le BA(OH)2.
Comme tu peux le voir, ce qui revient dans les produits est le H2O (eau). :)
Tu dois alors résoudre l'équation en l'équilibrant.
Par exemple, si on reprend la première équation:
HCl+NaOH → NaCl + H2O
- On commence par la molécule HCl : On a un H et un Cl
- On prend la molécule NaOH : On a un Na et un O et un H
- On fait le total : 2H, 1O, 1Na, 1Cl
- On résout l'équation en créant un sel et de l'eau : NaCl et H2O.
Tu trouveras une vidéo qui te donnera des trucs pour bien balancer ton équation au lien suivant: https://www.alloprof.qc.ca/fr/eleves/bv/sciences/le-balancement-d-une-equation-chimique-s1072
Tu verras, celle que tu as est un peu plus complexe à équilibrer, mais je suis certaine que tu vas y arriver! Le truc est de s'assurer de ne rien oublier!:)
Bonne résolution!
Sarah G