Best Of

Bonjour , le numéro 10 me pose problème à cause du ''dans 10 ans et dans 5 ans '' ainsi eu ''le trois quarts de son âge''. Merci de m'aider!

Ce contenu est protégé par le droit d'auteur. Toute reproduction à l'extérieur des forums Alloprof est interdite et pourra être considérée comme une violation du droit d'auteur.

Bonjour,

Commence par additionner tes deux fractions comme cela :

x/4 + x/3 = x*3/4*3 + x*4/3*4 = 3x/12 + 4x/12 = 7x/12

Par la suite, tu peux résoudre cela : 7x/12 = 14

Bonne journée :)

Salut ElfeArtistique!

Quand tu veux faire une multiplication avec les nombres négatifs, il faut normalement se fier au nombre. (s'il est négatif ou positif).

Si ton opération est -4x-4, tu multiplies deux nombres négatifs, alors ça devrait te donner un nombre positif; 16.

Pour le cas de -4x4, là tu multiplies un négatif avec un positif alors ça reste dans les négatifs. Techniquement, tu additionnes quatre fois ton -4, alors cette fois c'est -16.

Pour ta question avec les exposants, en "exposant" un chiffre tu le multiplie par lui même, le nombre de fois qu'il est écrit en haut. Si tu dis (-4) exposant en 2, tu fais -4x-4, car tu multiplie ton chiffre de base, qui est dans ce cas le -4. Ce qui donne justement 16! Un truc pour les exposant: Tu peux te baser sur le nombre au exposant pour savoir si la réponse est positive ou négative, parfois! (pair/impair)

Désolée si mon message était plutôt long, j'espère que ça répond à ta question même s'il y a déjà 5 réponses....

• Gobelin Romantique :)

Oui, c'est exactement ça! Par exemple (-2) exposant en 4 égal à -2×-2×-2×-2 et vu que le nombre exposant est positif cela égal à 2×2×2×2= 16. Si jamais il est négatif et que le nombre exposant est impair, la réponse a la fin seras négatif. Ex. (-2) exposant 3 égal à -8.

N'oublie pas que si le chiffre est positif il reste positif même si il est exposé en un nombre impair. (3) exposant 3 = 27

Allo. je pense pouvoir t'aider.

Pour ton: (-4) exposant 2, ca donne un produit positif

c'est un peu comme une réduction.

tu dois enlever les paranthèses et faire -4exposant 2 qui donne -16

et pour ton -4x-4, ca va te donner un nombre positif parceque deux nombres négatis multipliés ensemble donne toujours un nombre positif

jespere que mon explication te sera utile

Allo !

Dans le PEMDAS il y a des règles ( autre que l'ordre )

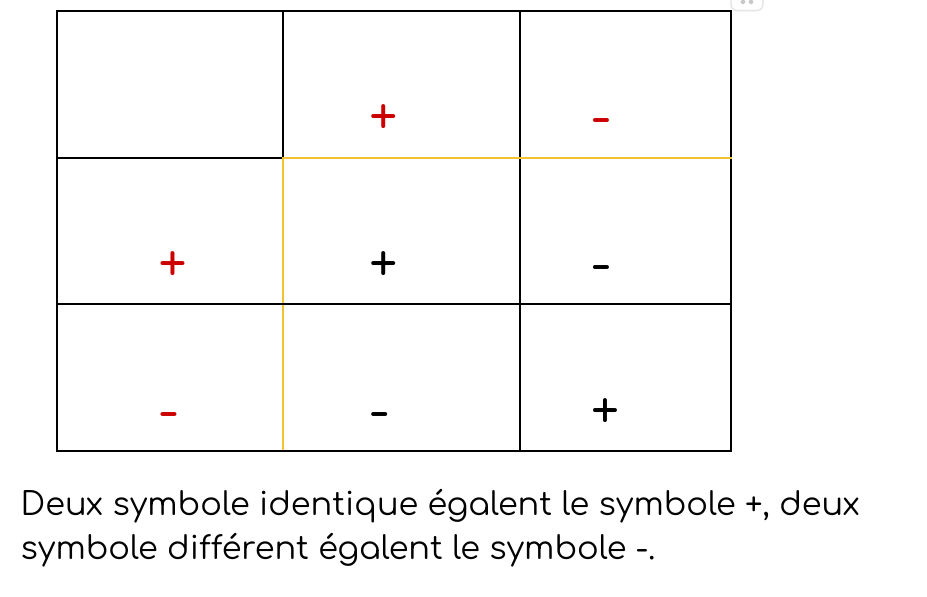
Déjà le -4 x -4, il faut quje tu retienne ça :

Ce contenu est protégé par le droit d'auteur. Toute reproduction à l'extérieur des forums Alloprof est interdite et pourra être considérée comme une violation du droit d'auteur.

Donc - et - sont identiquent se qui selon le tableau égale +.

4 x 4 = 16

Réponse : 16

Si celà avait été : - 4 + 4

+ et - sont différent se qui selon le tableau égale -.

4 x 4 = 16

Réponse : -16

Pour le -4 exposent 2 :

-4 exposent 2 = -2 x -2

Donc - et - ( pareille ) = +

2 x 2 = 4

Réponce: 4

J'espère t'avoir aider !

Allo! Je vien de conclure le chapitre sur les entiers négatifs et je peux t'aider! Alors pour le premier (-4) a la 2 on fait (-4) fois (-4), pour savoir si le résultat est négatif ou positif ici est un tableau qu'on peux utiliser pour les multiplications et les divisions

+ fois/divisé par - : donc la phrase l'ami de mon ennemi est mon ennemi donc la réponse sera négative

+ fois/divisé par + = l'ami de mon ami est mon ami donc la réponse est +

un nombre négatif fois/divisé par un autre nombre négatif fait alors la phrase : l'ennemi de mon ennemi est mon ami ( - fois/divisé par - = +)

Donc (-4) fois (-4) (l'ennemi de mon ennemi est mon ami) donc on fait -4 fois -4 qui donne 16!

Pour la deuxième question, mon seul truc pour s'améliorer dans les chaines d'opérations , c'est de s'exercer beaucoup et surtout de comprendre le pemdas/pedmas et de comprendre comment les nombres négatifs fonctionnent.

J'espère que cela t'a aidé :)

Salut!

Pour résoudre une équation, tu dois toujours placer les termes semblables d'un côté de l'équation, et les constantes de l'autre côté.

Dans ton exemple :

$$  -2b+6=3b-9 $$

Les termes semblables sont les termes ayant les mêmes variables (les mêmes inconnus). et ces variables sont affectées des mêmes exposants. Donc, nos termes semblables sont ici \(-2b\) et \(3b\), puisqu'ils contiennent tous les deux la variable b affectée d'un exposant 1.

Les constantes sont les termes qui ne contiennent pas de variables, soit ici \(6\) et \(-9\).

Notre but sera d'abord de placer d'un côté de l'égalité les deux termes semblables, et de l'autre côté les constantes. Pour ce faire, nous allons commencer par déplacer un des deux termes semblables de l'autre côté (peu importe lequel), et ce, en effectuant l'opération inverse.

Déplaçons \(-2b\) du côté droit de l'égalité. Puisque l'opération inverse d'une soustraction est une addition, nous allons devoir additionner \( 2b\) de chaque côté de l'équation, comme ceci :

$$  -2b+6+2b=3b-9+2b $$

En l'additionnant de chaque côté, cela nous permet de l'éliminer du côté gauche de l'équation :

$$  6=3b-9+2b $$

On a ainsi déplacé le terme \(2b\) afin qu'il soit du même côté que son terme semblable.

Passons maintenant aux constantes. Nous allons déplacer la constante \(-9\) de l'autre côté. Puisque l'opération inverse d'une soustraction est une addition, nous allons donc additionner \(9\) de chaque côté :

$$  6+9=3b-9+2b+9 $$

$$  6+9=3b+2b $$

On a ainsi réussi à placer nos termes semblables d'un côté et nos constantes de l'autre! La prochaine étape sera d'additionner les constantes, et d'additionner les coefficients des termes semblables.

$$  15=3b+2b $$

$$  15=(3+2)b $$

$$ 15=5b$$

Finalement, la dernière étape sera d'éliminer le coefficient de la variable b, soit \(5\), et ce, en effectuant l'opération inverse d'une multiplication, soit une division :

$$ \frac{15}{5}= \frac{5b}{5} $$

$$3 = b $$

$$ b = 3$$

Voilà! Voici des fiches sur ces notions qui pourraient t'être utiles :

• La résolution d'équations et d'inéquations | Secondaire | Alloprof
• Algèbre - Expressions algébriques | Alloprof

J'espère que c'est plus clair pour toi! Sinon, n'hésite pas à nous réécrire! :)