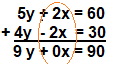Best Of

bonjour,

Tout d'abord, la substitution s'utilise quand tu peux substituer une variable par sa valeur connue. tu dois donc avoir une des deux variables isolée dans une équation. - ex. 2x+y=70 et x=3y) tu vas faire remplacer le x par 3y dans ton équation tu vas te retrouver avec 2(3y)+y=70, à partir de quoi tu pourras isoler la variable y pour en trouver la valeur 6y+y=70, 7y=70, y=10 , puis remplacer la valeur de y dans une équation pour trouver la valeur de x. x=3y , x=3(10), x=30 donc x=30 et y=10

Ensuite, la comparaison, tu dois comparer les deux équations. elles auront toutes les deux la même variable d'isoler. - Ex. y=3x+3 et y=2x+13 . comme c'est la même variable, elle a forcément la même valeur dans les deux équations (y=y). comme les deux équations sont égales à y, les deux équations sont équivalentes. tu peux donc utiliser 3x+3 = 2x+13 pour isoler la variable x. 3x+3-3=2x+13-3, 3x=2x+10, 3x-2x=2x-2x+10 , 1x=10 donc x=10, puis tu remplaces x par 10 dans une de tes deux équations, y=2(10)+13 , y=20+13, y=33 donc x=10 et y=33

Finalement, la réduction ou élimination, est un peu plus complexe, mais tu réduit / élimine une des deux variables. Pour ce faire tu alignes tes deux équations une au dessus de l'autre et fait une soustraction (ou une addition), jusqu'à ce que tu puisses éliminer une des deux variable. c'est possible que tu ais à faire quelques manipulations pour avoir une variable équivalentes. - Ex 2y-x=15 et 5y+2x=60 pour pouvoir éliminer une variable, tu devras t'arranger pour avoir deux variables identiques, ici tu peux faire x2 dans toute la première équation pour avoir le "2x" dans les deux. Attention de bien le faire de les deux côtés de l'équation. (2y-x=15)x2 donne 4y-2x=30 . Ensuite tu alignes et comme une de tes variables x est négatif, tu feras une addition. (4y-2x=30) + (5y+2x=60) , comme tu as un nombre négatif dans une des équations, tu feras une addition plutot qu'une soustraction pour éliminer la variable x.

Ce contenu est protégé par le droit d'auteur. Toute reproduction à l'extérieur des forums Alloprof est interdite et pourra être considérée comme une violation du droit d'auteur.

C'est ainsi que tu te retrouves avec 9y=90 et que tu peux donc isoler y. 9y/9=90/9 , y=10. puis remplacer la valeur de y dans une des équations initiales pour trouver la valeur de x.

2y-x=15. 2(10)-x=15, 20-x=15, 20-20-x=15-20, -x = -5, -x/-1 = -5/-1, x=5 donc x=5 et y=10.

J'espère que ça t'aide un peu !

Bonjour,

La principale différence est que l'expression algébrique est juste une combinaison de nombres et de lettres, tandis que l'égalité et l'équation utilisent un signe "=" pour montrer une relation entre deux expressions. Une équation, en particulier, contient souvent une ou plusieurs inconnues que nous essayons de résoudre.

expression algébrique: 2x + 3

équation algébrique: 2x + 3 = 7

Salut :D

Ça nous fait toujours extrêmement plaisir. :)

Ce contenu est protégé par le droit d'auteur. Toute reproduction à l'extérieur des forums Alloprof est interdite et pourra être considérée comme une violation du droit d'auteur.

Je lui passe le mot. Bonne journée à toi :D

@renard,

La méthode de réduction est préférable car il n est pas nécessaire d isoler y.

La résolution de systèmes d'équations linéaires

Bonjour,

La forme y = ax + b représente une droite sur un graphique. "a" est la pente de la droite et "b" est l'ordonnée à l'origine, c'est-à-dire la valeur de y lorsque x est égal à 0.

Pour isoler y, tu dois utiliser la technique de la balance disponible ici :

Malheureusement, nous n'avons pas d'exercices de ce genre. Cependant, tu peux te créer des équations et t'entraîner à les mettre sous la forme y = ax + b. Utilise différentes valeurs pour a et b et essaie de résoudre l'équation pour y.

J'espère que ces conseils te seront utiles.

Bonne journée

Salut :D

Il n'y a vraiment aucun problème. :) Pose autant de questions que tu le souhaites.

24 pièces

première pile : 1 * 1$

deuxième pile : (x+1) *0,25$

troisième pile : (x+2) * 0,10$

quatrième pile : (x+3) *0,05$

Il nous reste 23 pièces à séparer en trois piles, qui ont chacune plus de pièces que la précédente (au minimum 1 de plus). La plus grosse somme sera la possibilité où on a le plus de 25 sous possible.

On y va par essai-erreur. En considérant qu'il y a toujours plus de pièces dans chaque pile vers la droite. Prenons x = 4.

deuxième pile : (4+1) *0,25$

troisième pile : (4+2) * 0,10$

quatrième pile : (4+3) *0,05$

Ça nous donne une somme de (5+6+7= 17). Ce n'est pas ce qu'on cherche, on veut 23 pièces.

deuxième pile : (5) *0,25$

troisième pile : (6) * 0,10$

quatrième pile : (7) *0,05$

On recommence.

Prenons x = 5.

deuxième pile : (5+1) *0,25$

troisième pile : (5+2) * 0,10$

quatrième pile : (5+3) *0,05$

Donc,

deuxième pile : (6) *0,25$

troisième pile : (7) * 0,10$

quatrième pile : (8) *0,05$

On a une somme de (6+7+8=21).

On a donc trouvé le nombre de 0,25$, soit 6.

Ensuite, on peut ajouter une pièce de chaque (0,10$ et 0,05$) pour se rendre jusqu'à 23 en respectant les contraintes.

La répartition finale est alors :

première pile : 1 * 1$

deuxième pile : (6) *0,25$

troisième pile : (8) * 0,10$

quatrième pile : (9) *0,05$

Cela donne bien une somme de 24 pièces (1 + 6 + 8 + 9), et chaque pile en a plus que la précédente.

La somme maximale donne (1*1$ + 6*0,25$ + 8*0,10$ + 9*0,05$).

Je te laisse la calculer :D

Pour le deuxième exercice, tu pourrais reproduire les petits carrés avec une feuille de papier et les découper. Ça te permettra de manipuler les pièces, et d'observer quelle forme tu peux créer. Chaque fois que tu trouves une forme, dessine-la à part sur une feuille.

Bonne résolution :) À ta prochaine question :D