Best Of
Re: Question
Salut!
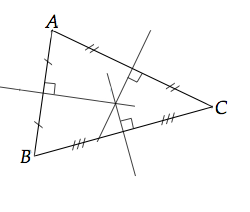
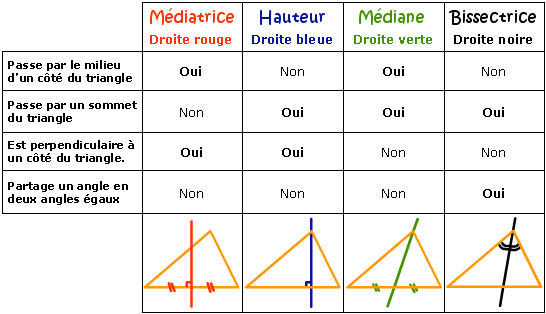
Attention, la médiatrice est une droite qui coupe un côté en deux segments égaux et forme un angle droit. Elle ne passe pas nécessairement par un sommet.
Donc, la médiatrice du segment AC ne passe pas nécessairement par le point B!
Pour trouver l'équation de la médiatrice de AC, il ne faut PAS trouver la règle avec le point B et le point milieu du segment AC. En faisant ça, tu trouves l'équation d'une médiane, et non d'une médiatrice! Tu dois plutôt trouver la pente de la droite AC, puis trouver l'opposé et l'inverse de cette pente, ce qui te donnera la pente de la médiatrice, qui est une droite perpendiculaire à AC.
Voici une fiche qui pourrait t'être utile : L'équation de droites parallèles ou perpendiculaires | Secondaire | Alloprof
Ensuite, une fois que tu connais la pente de la médiatrice, tu peux trouver l'équation complète à l'aide du point milieu de la droite AC par lequel passe la médiatrice.
Je te laisse réessayer avec ces indices. Si tu n'arrives pas à obtenir la bonne réponse, tu peux nous réécrire en nous envoyant une photo de ta démarche, ça nous fera plaisir de t'aider! :)
Re: Question
Bonjour,
Merci d'utiliser nos services!
Nous sommes très heureux de voir que tu apprécies nos services!
N'hésites surtout à nous réécrire si tu as d'autres questions!
Zachary T. :)
Re: Question
Bonsoir PicComique9971! 🙂
Merci pour ta question!
Si on regarde bien, sous ta racine, tu as 1 − sin²θ.
Cette expression apparaît dans une identité trigonométrique très connue :
sin²θ + cos²θ = 1
Si on isole cos²θ, on obtient :
1 − sin²θ = cos²θ
Donc, la racine de cos²θ donne cosθ.
J’espère que ça t’aide à mieux comprendre! 🙂
Je te souhaite une bonne soirée!
Si tu as d’autres questions, n’hésite pas à revenir nous voir! 😀
Re: Question
Bonjour PuceAgile, merci de nous avoir posé(e) une question 😊!
Alors voici des trucs pour t'aider !
Si tu veux bien métriser une matière premièrement il faut que tu la pratique jusqu'à ce que tu sois allaise avec celle-ci. Voici mon petit truc pour apprendre par coeur la matière.
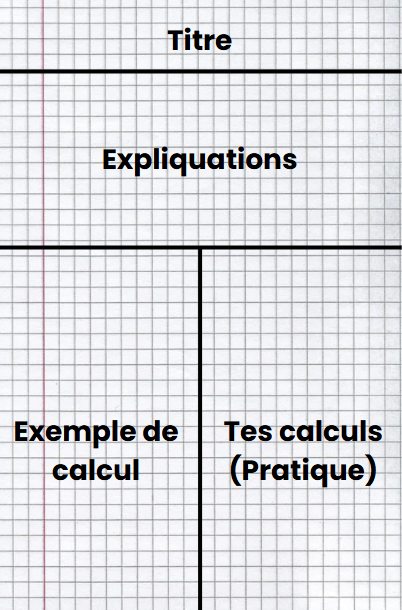
1) Je commence par séparer une feuille de note en quatre 4⃣ sections. La première va être pour identifier la matière que tu veux apprendre (en gros un titre). La deuxième va être les explications de ta matière (comment faire tes calculs ect.). La troisième section va être pour des exemples de calculs/exercices. Et finalement la dernière va être pour que tu puisse te pratiquer par toi même.
Voici un exemple de fiche que tu pourrais te créer ! 😊
J'espère t'avoir aidé(e), bonne chance pour ton examen tu es capable ! 😊
Re: Question
les arteres transportes le sang du coeur aux organes alors que les veines ramene le sang des organes vers le coeur.
arteres; sang coeur-->organes
veine; sang organes-->coeur
Question
Merci pour les prof qui sont venu dans l école saint bernadette soubirou je suis un éléve et 2 prof sont venu et nous on bien aider☺️☺️☺️☺️☺️
Question
Comment je peux trouver la règle d'un fonction exponentielle si j'ai juste le y et la base?
( dans mon cas la variable y=911,25$ et la base 1,5)
La situation veut qu'on trouve le nombre d'heure si le prix est des 911,25$ et le problème dit je cite, "le coût du nettoyage du polluant b après le premier incident était de 911,25$".
x:temps écoulé depuis le déversement
y:coût du nettoyage
merci d'avance :)
Re: Question
Alloprof est vraiment pertinent et d'une aide cruciale en effet! N'hésite pas à poser tes questions si tu en as! ;)