Best Of
Re: Question
Salut!
Avant de remplacer x par -4y/5 dans la seconde équation, je te conseille de commencer par la simplifier.
$$ \frac{ 5-x}{ 100} + \frac{ -x}{200 } + \frac{ -x}{ 400} + \frac{ y-x}{ 1000}=0$$
Tu peux commencer par séparer la première fraction en deux :
$$ \frac{ 5}{ 100} + \frac{-x}{ 100} + \frac{ -x}{200 } + \frac{ -x}{ 400} + \frac{ y-x}{ 1000}=0$$
Puis la dernière :
$$ \frac{ 5}{ 100} + \frac{-x}{ 100} + \frac{ -x}{200 } + \frac{ -x}{ 400} + \frac{ y}{ 1000}+ \frac{ -x}{ 1000}=0$$
On peux simplifier la constante et la déplacer de l’autre côté de l’équation :
$$ \frac{ 1}{ 20} + \frac{-x}{ 100} + \frac{ -x}{200 } + \frac{ -x}{ 400} + \frac{ y}{ 1000}+ \frac{ -x}{ 1000}=0$$
$$ \frac{-x}{ 100} + \frac{ -x}{200 } + \frac{ -x}{ 400} + \frac{ y}{ 1000}+ \frac{ -x}{ 1000}= -\frac{ 1}{ 20} $$
Ensuite, on peut réécrire les termes afin de bien voir le coefficient de la variable :
$$ \frac{-1}{ 100} x+ \frac{ -1}{200 } x+ \frac{ -1}{ 400} x+ \frac{ 1}{ 1000}y+ \frac{ -1}{ 1000}x= -\frac{ 1}{ 20} $$
On peut maintenant additionner tous les termes semblables. Pour cela, on additionne leur coefficient :
$$( \frac{-1}{ 100} + \frac{ -1}{200 } + \frac{ -1}{ 400}+ \frac{ -1}{ 1000})x+ \frac{ 1}{ 1000}y= -\frac{ 1}{ 20} $$
Une fois que ton équation est simplifiée, tu pourras alors remplacer x par -4y/5 et résoudre l’équation résultante plus facilement.
Je te laisse continuer avec ces indices. J’espère que c’est plus clair pour toi! :)
Re: Question
Bonjour AigleAgile9084! :)
Merci pour ta question!
Après avoir consulté différents sites de cégep qui offrent la technique en soins infirmiers, je peux te confirmer que l’admission exige les sciences enrichies (STE) de 4e secondaire. De plus, en 5e secondaire, il est obligatoire de réussir le cours de chimie. Les mathématiques, quant à elles, ne devraient pas affecter tes chances d’être admis.
Par contre, si jamais tu n’as pas suivi toutes les matières requises, tu pourras faire un cours de mise à niveau pendant l’été ou encore reprendre les sciences enrichies en secondaire 5 si ton école les offre. Cela ne posera aucun problème!
J'espère avoir répondu à tes questions! Si tu as d'autres questions, n'hésite pas à revenir nous voir! :D
Je te souhaite une belle journée!
Re: Question
Si tu as de la difficulté avec ce type d'exercice, je te suggère de procéder méthodiquement pour ne pas te mêler avec tous ces termes:
(3x² + 5y)² - 6y(5x² - 3y)
= (3x² + 5y)(3x² + 5y) -6y(5x²) - 6y(-3y)
= 3x²(3x² + 5y) + 5y(3x² + 5y) - 30x²y + 18y²
= 9x^4 + 15x²y + 15x²y + 25y² - 30x²y + 18y²
on regroupe les termes semblables (les termes en x²y s'annulent)
= 9x^4 + 43y²
Re: Question
Bonjour CielTurquoise4865,
Je vais t'aider à comprendre et à savoir comment résoudre ces sortes de problèmes étapes par étapes.
Étape 1: Supprimer les doubles négations.
-(-5): Le moins devant le moins transforme -5 en +5.
-(-11): Le moins devant le moins transforme -11 en +11.
Alors, l'équation devient: 5-(-11).
Étape 2: Trouver la réponse.
Maintenant qu'on sait que un moins devant un autre moins transforme un nombre négatif en un nombre positif, on peut facilement trouver la réponse de l'équation.
Donc: 5-(-11) équivaut à 5+11=16.
J'espère que mes explications t'ont aidées.
-WapitiTenace8028
Au besoin, consulte la fiche sur les nombres entiers, section nombres opposés.
https://www.alloprof.qc.ca/fr/eleves/bv/mathematiques/les-nombres-entiers-m1023
Question
mon fils a la classe d'accueil 2eme année je voudrais aider la licture et l'écriture quels son les moyens ou les methodes que je devrais utiliser avec lui
sachant qu'il n'aime pas lire et ecrire
Re: Question
Bonjour, DiamantLogique7902!
Si vous avez commencé par la fiche L'ordre croissant et décroissant, je vous conseille de poursuivre avec Ordonner des nombres naturels.
Placer les nombres en ordre croissant revient à placer les nombres du plus petit au plus grand.
$$ 0\ <\ 1\ <\ 2\ <\ 3\ <\ 4\ <\ 5\ <\ 6\ <\ ... $$
Placer les nombres en ordre décroissant revient à placer les nombres du plus grand au plus petit.
$$ ...\ >\ 6\ >\ 5\ >\ 4\ >\ 3\ >\ 2\ >\ 1\ >\ 0 $$
Pour comprendre ce sujet, mieux vaut s'accompagner d'illustrations ou d'une droite numérique.
Prends une feuille, dessine par exemple des paquets différents de pommes en indiquant combien il y en a dans chaque et demande-lui quel groupe en a le moins. Il placera ainsi en ordre croissant.
https://www.alloprof.qc.ca/fr/eleves/bv/mathematiques/ordonner-les-nombres-naturels-m1026
N'hésite pas à poser d'autres questions!
Re: Question
Bonsoir, GalliumGamma6090!
Révisons le vocabulaire de l'algèbre.
- Une variable est une lettre qui peut prendre différentes valeurs.
- Un coefficient est un nombre qui multiplie une ou plusieurs variables.
Le degré d'une expression algébrique correspond à la valeur des exposants des variables.
Voyons des exemples dont tu peux t'inspirer et corriger certaines réponses.
https://www.alloprof.qc.ca/fr/eleves/bv/mathematiques/du-monome-au-polynome-m1069
N'hésite pas à poser d'autres questions!
Re: Question
Salut PandaArtistique !
C'est très différent. La chimie s'intéresse aux molécules, à leurs réactions, leur constitution etc, tandis que la physique étudie les forces, l'énergie, les atomes, les constituants les plus petits de la matière (physique quantique) comme leurs compositions les plus grandes (astronomie), etc.
De rien
Re: Question
Salut!
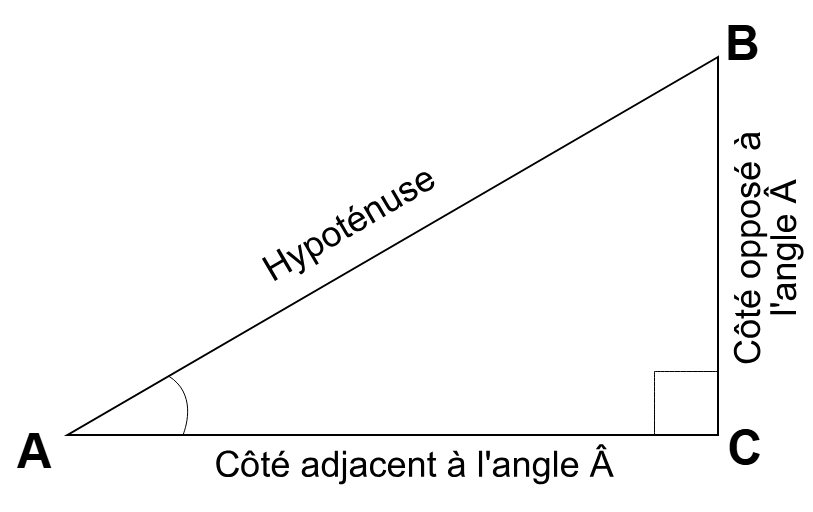
Un triangle rectangle est composé d'une hypoténuse, le côté le plus long, et de deux cathètes.
On a trois morceaux initialement : 21 cm, 42 cm et 45 cm. En d'autres mots, le plus long morceau est celui de 45 cm.
Si on enlève une certaine longueur de x cm à chaque morceau, ils raccourciront tous, mais le plus long morceau initial (celui de 45 cm) restera tout de même le plus long des trois morceaux finaux, avec une longueur finale de (45-x) cm. Ainsi, on peut conclure que l'hypoténuse de notre triangle rectangle final sera de (45-x). Les cathètes sont donc (42-x) cm et (21-x) cm.
On peut alors poser l'équation suivante en utilisant le théorème de Pythagore :
$$(45-x)^2=(42-x)^2+(21-x)^2$$
Il ne reste plus qu'à résoudre cette équation pour trouver x, la longueur enlevée aux morceaux originaux!
J'espère que c'est plus clair pour toi! :)
Re: Question
Salut,
Merci d'utiliser la zone d'entraide.
C'est une très bonne question !
C'est vrai que ces deux classes de mots peuvent se ressembler, puisqu'elles sont toutes les deux invariables !
Toutefois, voici une liste de chacune d'entre elle :
-Prépositions : à, de, dans, pour, sans, sous, sur, etc
-Adverbes : hier, tellement, très, rapidement, vite, ne...pas
Comme tu peux le constater, la préposition est souvent plus courte que l'adverbe! L'adverbe, quant à lui, finit souvent par «ment».
L'adverbe modifie un mot (verbe, adverbe ou adjectif).
ex : Elle est belle ; elle est très belle.
ex2 : Il marche ; il marche rapidement
De plus, l'adverbe est souvent facultatif, c'est à dire qu'on peut l'enlever :)
La préposition, elle, sert à unir deux mots.
ex : Je viens de Montréal, je viens Montréal
ex2 : Je donnerai ce cadeau à Louise; je donnerai ce cadeau Louise
Comme tu peux le voir, on ne peut généralement pas l'enlever ! :D
**** Un truc : si tu n'es pas certain de la classe d'un mot, essaie de le remplacer par un autre mot de la même classe! :)
Voilà :D Maintenant tu sais comment repérer un adverbe et une préposition ! ;p Tu peux consulter les fiches suivantes pour obtenir plus d'exemples :
Pour ta deuxième question, je ne suis pas certaine de bien comprendre. N'hésite pas à nous réécrire pour ajouter des précisions. D'ici là, tu peux consulter la fiche sur les conjonctions de subordination:
N'hésite pas si tu as d'autres questions !
Karen