Best Of
Question
Bonsoir 🙂
Lundi, j’ai un examen sur les risques naturels et j’ai encore des doutes concernant la différence entre un risque naturel et une catastrophe naturelle. Pour mieux comprendre, j’ai consulté votre fiche et votre vidéo, mais je n’ai malheureusement rien compris 😞. J’aurais vraiment besoin de votre aide, s’il vous plaît.
Merci de votre compréhension :)
Question
À quoi les français et les autochtones se sont engagés précisément lors de l'alliance franco-autochtone de 1603?
Question
Quel est l'établissement français dont la fondation marque le passage de la période des Premiers occupants au Régime français ?
Question
Ce n'est pas une question que je vous pose mais je voulais vous remercier pour tout le soutien que vous nous donner nous les élèves de primaire a secondaire. J'aimerais vous remercier car votre aide dans la zone d'entraide, vos fiches, vos vidéo, vos exercice, et jeu m'aide énormément enfin nous aides a mieux comprendre les notion un peut plus compliquer pour nous. Vraiment MERCI pour l'aide que vous nous apportée l'équipe Alloprof.
DiamantAlpha2246 2025-09-27
Re: Question
Bonsoir, R2D2Turbo3256!
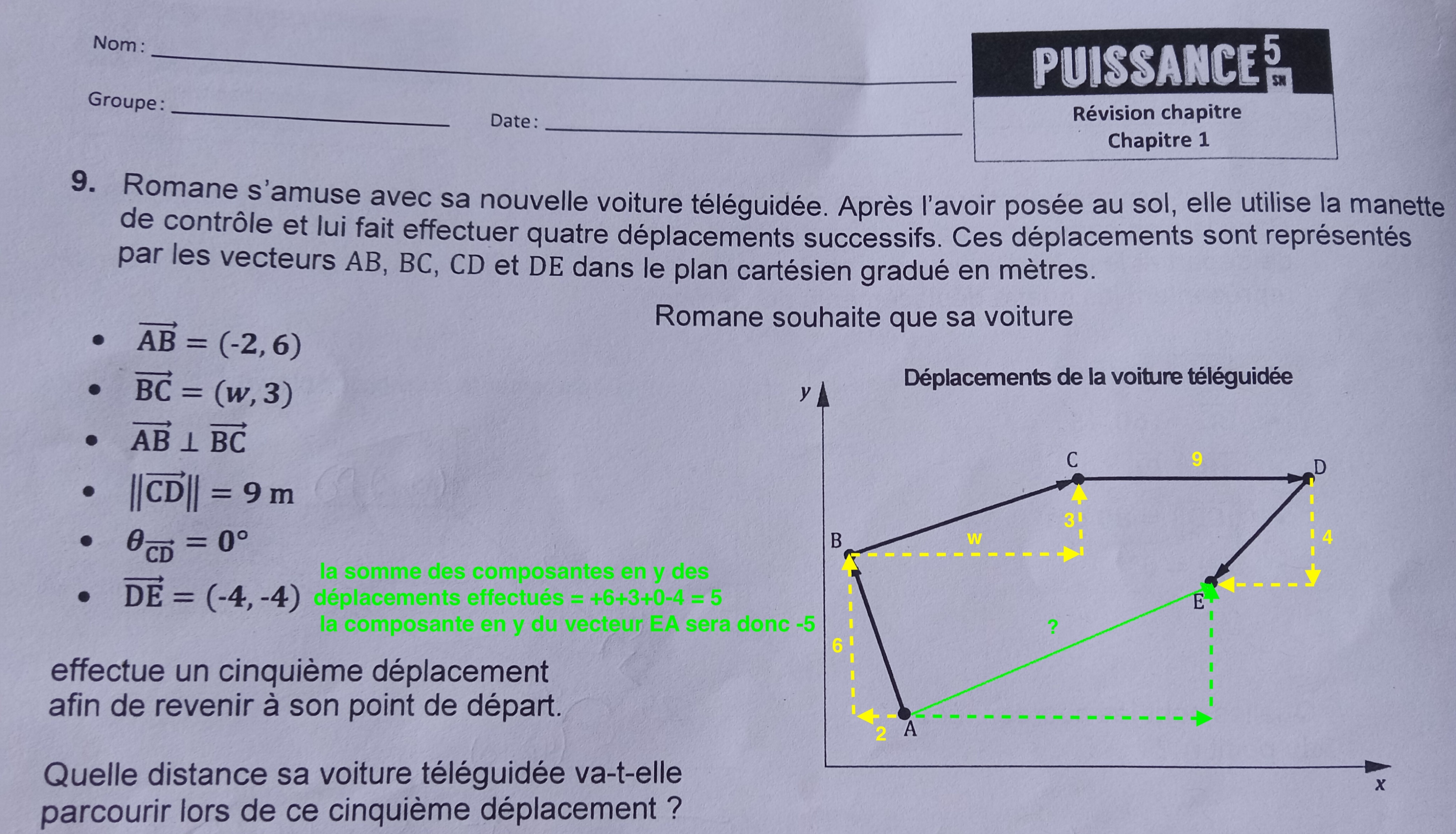
Trouve les composantes du vecteur résultant de tous les déplacements: le vecteur recherché est de sens contraire.
Connaissant les composantes, tu peux trouver la distance (qui est la norme de ce vecteur) en utilisant le théorème de Pythagore.
Voici comment obtenir une des composantes.
Tu devrais pouvoir terminer sans peine.
Pour w, utilise la formule des vecteurs orthogonaux.
Re: Question
Bonsoir, DauphinAlpha2019!
Il faut premièrement écrire toutes les bases selon la plus petite base possible, donc plus petit commun multiple. Dans ce cas-ci, c’est 2.
- On écrirait donc \( 16^3 \) comme ça: \( (2^4)^3 \) .
- Pour \( 8^2 \), on l’écrirait comme ça: \( (2^3)^2 \).
- Le dénominateur, lui, ne change pas.
N’oublie pas tes parenthèses où je les ai mis. Je te laisse faire le reste.
Indice: multiplication des exposants.
Recontacte nous si tu veux plus de clarifications.
Re: Question
Bonjour,
Merci pour la question!
Il n'existe pas de technique spéciale pour apprendre les tables de division. C'est avec de la pratique qu'on les apprend. Cependant, il existe quelques trucs qui peuvent aider à les apprendre par cœur.
Voici une fiche explicative qui explique les trucs en question :
N'hésite pas si tu as d'autres questions!
Zachary T. :)
Re: Question
Bonjour XwingHumble9168,
Merci de faire appel à la Zone d'entraide!
Voici les étapes de divisons d'un polynome par un binome:
1- Ordonner les termes du dividende en ordre décroissant (du plus grand degré au plus petit).
2- Diviser le premier terme du dividende par le premier terme du diviseur.
3- Placer le résultat de cette division sous le diviseur.
4- Multiplier ce résultat par tout le diviseur.
5- Soustraire ce résultat du dividende (attention aux signes positifs et négatifs ! !)
6- Abaisser les termes restants du dividende au même endroit que le résultat de cette soustraction.
7- Répéter les étapes 2 à 6 jusqu'à ce que le dividende soit plus petit que le diviseur (si possible, jusqu'à 0).
8- Au besoin, rajouter le reste au résultat de façon adéquate.
Voici un lien vers encore plus d'informations pour mieux comprendre :
La division d'une expression algébrique par un binôme | Secondaire | Alloprof
N'hésite pas si tu as d'autres questions :)
RenardAdorable6678
Re: Question
Bonjour DiamantMauve134,
Merci d'utiliser la Zone d'entraide :)
Tout d'abord, il est important de savoir qu'une capitale est la ville la plus importante d'un pays, dans laquelle des décisions importantes se font, où le gouvernement travaille et généralement où se trouvent le président et le parlement. Normalement, il y a 1 capitale par pays, donc il y a le même nombre de capitales dans le monde que de pays (195 en ce moment). Attention, il y a quelques exceptions, mais tu peux facilement trouver les informations nécessaires sur Google, par exemple.
J'espère t'avoir aidé!
RenardAdorable6678